|
Physics-informed Neural Networks
Physics-informed neural networks (PINNs), also referred to as Theory-Trained Neural Networks (TTNs), are a type of universal function approximators that can embed the knowledge of any physical laws that govern a given data-set in the learning process, and can be described by partial differential equations (PDEs). Low data availability for some biological and engineering problems limit the robustness of conventional machine learning models used for these applications. The prior knowledge of general physical laws acts in the training of neural networks (NNs) as a Regularization (mathematics), regularization agent that limits the space of admissible solutions, increasing the Overfitting, generalizability of the function approximation. This way, embedding this prior information into a neural network results in enhancing the information content of the available data, facilitating the learning algorithm to capture the right solution and to generalize well even with a low amount of traini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
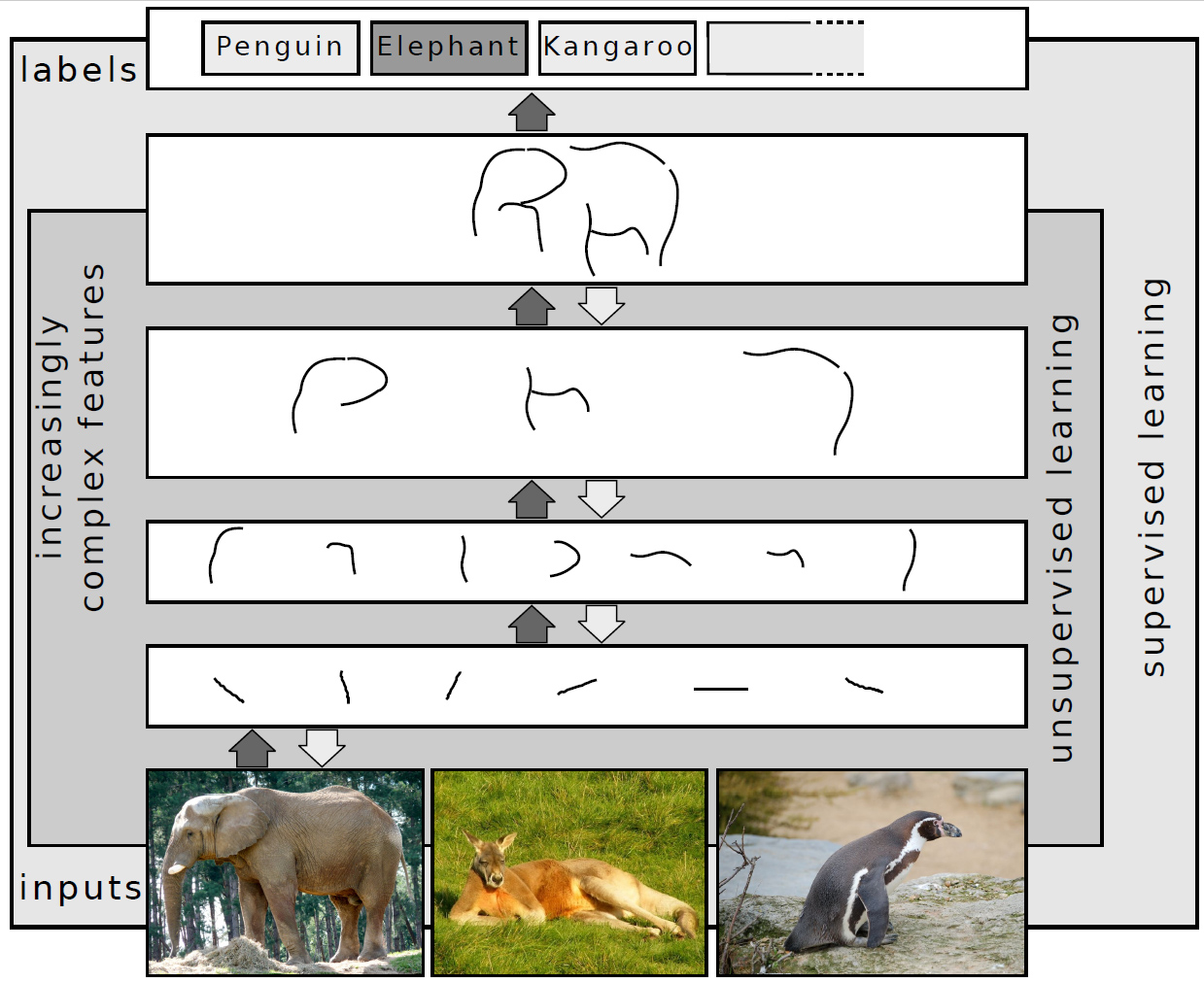
Deep Learning
Deep learning is a subset of machine learning that focuses on utilizing multilayered neural networks to perform tasks such as classification, regression, and representation learning. The field takes inspiration from biological neuroscience and is centered around stacking artificial neurons into layers and "training" them to process data. The adjective "deep" refers to the use of multiple layers (ranging from three to several hundred or thousands) in the network. Methods used can be either supervised, semi-supervised or unsupervised. Some common deep learning network architectures include fully connected networks, deep belief networks, recurrent neural networks, convolutional neural networks, generative adversarial networks, transformers, and neural radiance fields. These architectures have been applied to fields including computer vision, speech recognition, natural language processing, machine translation, bioinformatics, drug design, medical image analysis, c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
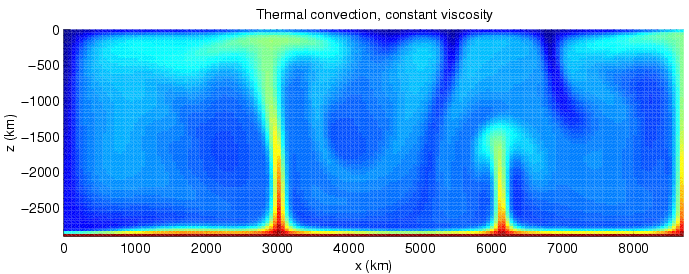
Heat Transfer
Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, Convection (heat transfer), thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species (mass transfer in the form of advection), either cold or hot, to achieve heat transfer. While these mechanisms have distinct characteristics, they often occur simultaneously in the same system. Heat conduction, also called diffusion, is the direct microscopic exchanges of kinetic energy of particles (such as molecules) or quasiparticles (such as lattice waves) through the boundary between two systems. When an object is at a different temperature from another body or its surroundings, heat flows so that the body and the surroundings reach the same temperature, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incompressible Flow
In fluid mechanics, or more generally continuum mechanics, incompressible flow is a flow in which the material density does not vary over time. Equivalently, the divergence of an incompressible flow velocity is zero. Under certain conditions, the flow of compressible fluids can be modelled as incompressible flow to a good approximation. Derivation The fundamental requirement for incompressible flow is that the density, \rho , is constant within a small element volume, ''dV'', which moves at the flow velocity u. Mathematically, this constraint implies that the material derivative (discussed below) of the density must vanish to ensure incompressible flow. Before introducing this constraint, we must apply the conservation of mass to generate the necessary relations. The mass is calculated by a volume integral of the density, \rho : : = . The conservation of mass requires that the time derivative of the mass inside a control volume be equal to the mass flux, J, acro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonidas J
Leonidas I (; , ''Leōnídas''; born ; died 11 August 480 BC) was king of the Ancient Greek city-state of Sparta. He was the son of king Anaxandridas II and the 17th king of the Agiad dynasty, a Spartan royal house which claimed descent from the mythical demigod Heracles. Leonidas I ascended to the throne in , succeeding his half-brother king Cleomenes I. He ruled jointly along with king Leotychidas until his death in 480 BC, when he was succeeded by his son, Pleistarchus. At the Second Greco-Persian War, Leonidas led the allied Greek forces in a last stand at the Battle of Thermopylae (480 BC), attempting to defend the pass from the invading Persian army, and was killed early during the third and last day of the battle. Leonidas entered myth as a hero and the leader of the 300 Spartans who died in battle at Thermopylae. While the Greeks lost this battle, they were able to expel the Persian invaders in the following year. Life According to Herodotus, Leonidas' mother was n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Extreme Learning Machine
Extreme learning machines are feedforward neural networks for classification, regression, clustering, sparse approximation, compression and feature learning with a single layer or multiple layers of hidden nodes, where the parameters of hidden nodes (not just the weights connecting inputs to hidden nodes) need to be tuned. These hidden nodes can be randomly assigned and never updated (i.e. they are random projection but with nonlinear transforms), or can be inherited from their ancestors without being changed. In most cases, the output weights of hidden nodes are usually learned in a single step, which essentially amounts to learning a linear model. The name "extreme learning machine" (ELM) was given to such models by Guang-Bin Huang who originally proposed for the networks with any type of nonlinear piecewise continuous hidden nodes including biological neurons and different type of mathematical basis functions. The idea for artificial neural networks goes back to Frank Rosenb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theory Of Functional Connections
The Theory of Functional Connections (TFC) is a mathematical framework for functional interpolation. It provides a method for deriving a functional—a function that operates on another function—which can transform constrained optimization problems into equivalent unconstrained ones. This transformation allows TFC to be applied to a wide range of mathematical problems, including the solution of Differential equation, differential equations. In this context, functional interpolation refers to the construction of functionals that always satisfy specified constraints, regardless of how the internal (or free) function is expressed. From interpolation to functional interpolation To provide a general context for the TFC, consider a generic interpolation problem involving n constraints, such as a differential equation subject to a boundary value problem (BVP). Regardless of the differential equation, these constraints may be Consistency, consistent or inconsistent. For instance, in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Assimilation
Data assimilation refers to a large group of methods that update information from numerical computer models with information from observations. Data assimilation is used to update model states, model trajectories over time, model parameters, and combinations thereof. What distinguishes data assimilation from other estimation methods is that the computer model is a dynamical model, i.e. the model describes how model variables change over time, and its firm mathematical foundation in Bayesian Inference. As such, it generalizes inverse methods and has close connections with machine learning. Data assimilation initially developed in the field of numerical weather prediction. Numerical weather prediction models are equations describing the evolution of the atmosphere, typically coded into a computer program. When these models are used for forecasting the model output quickly deviates from the real atmosphere. Hence, we use observations of the atmosphere to keep the model on track. Data ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symbolic Differentiation
In mathematics and computer science, computer algebra, also called symbolic computation or algebraic computation, is a scientific area that refers to the study and development of algorithms and software for manipulating mathematical expressions and other mathematical objects. Although computer algebra could be considered a subfield of scientific computing, they are generally considered as distinct fields because scientific computing is usually based on numerical computation with approximate floating point numbers, while symbolic computation emphasizes ''exact'' computation with expressions containing variables that have no given value and are manipulated as symbols. Software applications that perform symbolic calculations are called ''computer algebra systems'', with the term ''system'' alluding to the complexity of the main applications that include, at least, a method to represent mathematical data in a computer, a user programming language (usually different from the languag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Differentiation
In numerical analysis, numerical differentiation algorithms estimate the derivative of a mathematical function or subroutine using values of the function and perhaps other knowledge about the function. Finite differences The simplest method is to use finite difference approximations. A simple two-point estimation is to compute the slope of a nearby secant line through the points and . Choosing a small number , represents a small change in , and it can be either positive or negative. The slope of this line is \frac. This expression is Newton's difference quotient (also known as a first-order divided difference). The slope of this secant line differs from the slope of the tangent line by an amount that is approximately proportional to . As approaches zero, the slope of the secant line approaches the slope of the tangent line. Therefore, the true derivative of at is the limit of the value of the difference quotient as the secant lines get closer and closer to being a tange ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |