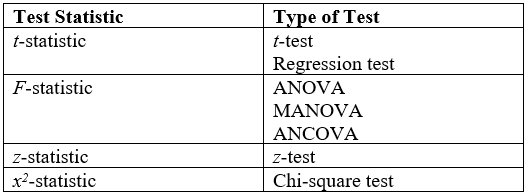
|
Pearson's Chi-squared Test
Pearson's chi-squared test or Pearson's \chi^2 test is a statistical test applied to sets of categorical data to evaluate how likely it is that any observed difference between the sets arose by chance. It is the most widely used of many chi-squared tests (e.g., Yates, likelihood ratio, portmanteau test in time series, etc.) – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900. In contexts where it is important to improve a distinction between the test statistic and its distribution, names similar to ''Pearson χ-squared'' test or statistic are used. It is a p-value test. The setup is as follows: * Before the experiment, the experimenter fixes a certain number N of samples to take. * The observed data is (O_1, O_2, ..., O_n), the count number of samples from a finite set of given categories. They satisfy \sum_i O_i = N. * The null hypothesis is that the count numbers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Test
A statistical hypothesis test is a method of statistical inference used to decide whether the data provide sufficient evidence to reject a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. Then a decision is made, either by comparing the test statistic to a critical value or equivalently by evaluating a ''p''-value computed from the test statistic. Roughly 100 specialized statistical tests are in use and noteworthy. History While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Choice of null hypothesis Paul Meehl has argued that the epistemological importance of the choice of null hypothesis has gone largely unacknowledged. When the null hypothesis is predicted by theory, a more precise experiment will be a more severe tes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Distribution
In statistics, the frequency or absolute frequency of an Event (probability theory), event i is the number n_i of times the observation has occurred/been recorded in an experiment or study. These frequencies are often depicted graphically or tabular form. Types The cumulative frequency is the total of the absolute frequencies of all events at or below a certain point in an ordered list of events. The Empirical probability, relative frequency (or ''empirical probability'') of an event is the absolute frequency Normalizing constant, normalized by the total number of events: : f_i = \frac = \frac. The values of f_i for all events i can be plotted to produce a frequency distribution. In the case when n_i = 0 for certain i, pseudocounts can be added. Depicting frequency distributions A frequency distribution shows a summarized grouping of data divided into mutually exclusive classes and the number of occurrences in a class. It is a way of showing unorganized data notably to sh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi-squared Distribution
In probability theory and statistics, the \chi^2-distribution with k Degrees of freedom (statistics), degrees of freedom is the distribution of a sum of the squares of k Independence (probability theory), independent standard normal random variables. The chi-squared distribution \chi^2_k is a special case of the gamma distribution and the univariate Wishart distribution. Specifically if X \sim \chi^2_k then X \sim \text(\alpha=\frac, \theta=2) (where \alpha is the shape parameter and \theta the scale parameter of the gamma distribution) and X \sim \text_1(1,k) . The scaled chi-squared distribution s^2 \chi^2_k is a reparametrization of the gamma distribution and the univariate Wishart distribution. Specifically if X \sim s^2 \chi^2_k then X \sim \text(\alpha=\frac, \theta=2 s^2) and X \sim \text_1(s^2,k) . The chi-squared distribution is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in constru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chi-square DistributionCDF-English
The term chi-square, chi-squared, or \chi^2 has various uses in statistics: *chi-square distribution, a continuous probability distribution *chi-square test, name given to some tests using chi-square distribution *chi-square target models, a mathematical model used in radar cross-section {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-distribution
In probability theory and statistics, the ''F''-distribution or ''F''-ratio, also known as Snedecor's ''F'' distribution or the Fisher–Snedecor distribution (after Ronald Fisher and George W. Snedecor), is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA) and other ''F''-tests. Definitions The ''F''-distribution with ''d''1 and ''d''2 degrees of freedom is the distribution of X = \frac where U_1 and U_2 are independent random variables with chi-square distributions with respective degrees of freedom d_1 and d_2. It can be shown to follow that the probability density function (pdf) for ''X'' is given by \begin f(x; d_1,d_2) &= \frac \\ pt&=\frac \left(\frac\right)^ x^ \left(1+\frac \, x \right)^ \end for real ''x'' > 0. Here \mathrm is the beta function. In many applications, the parameters ''d''1 and ''d''2 are positive integers, but the distribution is wel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Student's T
In probability theory and statistics, Student's distribution (or simply the distribution) t_\nu is a continuous probability distribution that generalizes the standard normal distribution. Like the latter, it is symmetric around zero and bell-shaped. However, t_\nu has heavier tails, and the amount of probability mass in the tails is controlled by the parameter \nu. For \nu = 1 the Student's distribution t_\nu becomes the standard Cauchy distribution, which has very "fat" tails; whereas for \nu \to \infty it becomes the standard normal distribution \mathcal(0, 1), which has very "thin" tails. The name "Student" is a pseudonym used by William Sealy Gosset in his scientific paper publications during his work at the Guinness Brewery in Dublin, Ireland. The Student's distribution plays a role in a number of widely used statistical analyses, including Student's -test for assessing the statistical significance of the difference between two sample means, the cons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Gamma Distribution
The generalized gamma distribution is a continuous probability distribution with two shape parameters (and a scale parameter). It is a generalization of the gamma distribution which has one shape parameter (and a scale parameter). Since many distributions commonly used for parametric models in survival analysis (such as the exponential distribution, the Weibull distribution and the gamma distribution) are special cases of the generalized gamma, it is sometimes used to determine which parametric model is appropriate for a given set of data. Another example is the half-normal distribution. Characteristics The generalized gamma distribution has two shape parameters, d > 0 and p > 0, and a scale parameter, a > 0. For non-negative ''x'' from a generalized gamma distribution, the probability density function is : f(x; a, d, p) = \frac, where \Gamma(\cdot) denotes the gamma function. The cumulative distribution function is : F(x; a, d, p) = \frac , \text \, P\left( \frac, \left( \fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Uniform Distribution
In probability theory and statistics, the discrete uniform distribution is a symmetric probability distribution wherein each of some finite whole number ''n'' of outcome values are equally likely to be observed. Thus every one of the ''n'' outcome values has equal probability 1/''n''. Intuitively, a discrete uniform distribution is "a known, finite number of outcomes all equally likely to happen." A simple example of the discrete uniform distribution comes from throwing a fair six-sided die. The possible values are 1, 2, 3, 4, 5, 6, and each time the die is thrown the probability of each given value is 1/6. If two dice were thrown and their values added, the possible sums would not have equal probability and so the distribution of sums of two dice rolls is not uniform. Although it is common to consider discrete uniform distributions over a contiguous range of integers, such as in this six-sided die example, one can define discrete uniform distributions over any finite set. Fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alpha Level
Type I error, or a false positive, is the erroneous rejection of a true null hypothesis in statistical hypothesis testing. A type II error, or a false negative, is the erroneous failure in bringing about appropriate rejection of a false null hypothesis. Type I errors can be thought of as errors of commission, in which the status quo is erroneously rejected in favour of new, misleading information. Type II errors can be thought of as errors of omission, in which a misleading status quo is allowed to remain due to failures in identifying it as such. For example, if the assumption that people are ''innocent until proven guilty'' were taken as a null hypothesis, then proving an innocent person as guilty would constitute a Type I error, while failing to prove a guilty person as guilty would constitute a Type II error. If the null hypothesis were inverted, such that people were by default presumed to be ''guilty until proven innocent'', then proving a guilty person's innocence would c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Significance Level
In statistical hypothesis testing, a result has statistical significance when a result at least as "extreme" would be very infrequent if the null hypothesis were true. More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is said to be ''statistically significant'', by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or observation that involves drawing a sample from a population, there is always the possibility that an observed effect would have occurred due to sampling error alone. But if the ''p''-value of an observed effect is less than (or equal to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degrees Of Freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary. Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the estimate of a parameter is called the degrees of freedom. In general, the degrees of freedom of an estimate of a parameter are equal to the number of independent scores that go into the estimate minus the number of parameters used as intermediate steps in the estimation of the parameter itself. For example, if the variance is to be estimated from a random sample of N independent scores, then the degrees of freedom is equal to the number of independent scores (''N'') minus the number of parameters estimated as intermediate steps (one, namely, the sample mean) and is therefore equal to N-1. Mathematically, degrees of freedom is the number of dimensions of the domain of a random vector, or e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency (statistics)
In statistics, the frequency or absolute frequency of an event i is the number n_i of times the observation has occurred/been recorded in an experiment or study. These frequencies are often depicted graphically or tabular form. Types The cumulative frequency is the total of the absolute frequencies of all events at or below a certain point in an ordered list of events. The relative frequency (or ''empirical probability'') of an event is the absolute frequency normalized by the total number of events: : f_i = \frac = \frac. The values of f_i for all events i can be plotted to produce a frequency distribution. In the case when n_i = 0 for certain i, pseudocounts can be added. Depicting frequency distributions A frequency distribution shows a summarized grouping of data divided into mutually exclusive classes and the number of occurrences in a class. It is a way of showing unorganized data notably to show results of an election, income of people for a certain region, sal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |