|
Obversion
In traditional logic, obversion is a "type of immediate inference in which from a given proposition another proposition is inferred whose subject is the same as the original subject, whose predicate is the contradictory of the original predicate, and whose quality is affirmative if the original proposition's quality was negative and vice versa".Quoted definition is from: Brody, Bobuch A. "Glossary of Logical Terms". ''Encyclopedia of Philosophy''. Vol. 5–6, p. 70. Macmillan, 1973. Also, Stebbing, L. Susan. ''A Modern Introduction to Logic''. Seventh edition, pp. 65–66. Harper, 1961, and Irving Copi's ''Introduction to Logic'', p. 141, Macmillan, 1953. All sources give virtually identical explanations. Copi (1953) and Stebbing (1931) both limit the application to categorical propositions, and in ''Symbolic Logic'', 1979, Copi limits the use of the process, remarking on its "absorption" into the Rules of Replacement in quantification and the axioms of class algebra. The quality ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Categorical Proposition
In logic, a categorical proposition, or categorical statement, is a proposition that asserts or denies that all or some of the members of one category (the ''subject term'') are included in another (the ''predicate term''). The study of arguments using categorical statements (i.e., syllogisms) forms an important branch of deductive reasoning that began with the Ancient Greeks. The Ancient Greeks such as Aristotle identified four primary distinct types of categorical proposition and gave them standard forms (now often called ''A'', ''E'', ''I'', and ''O''). If, abstractly, the subject category is named ''S'' and the predicate category is named ''P'', the four standard forms are: * All ''S'' are ''P''. (''A'' form) * No ''S'' are ''P''. (''E'' form) * Some ''S'' are ''P''. (''I'' form) * Some ''S'' are not ''P''. (''O'' form) A large number of sentences may be translated into one of these canonical forms while retaining all or most of the original meaning of the sentence. Greek inves ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Traditional Logic
In logic and formal semantics, term logic, also known as traditional logic, syllogistic logic or Aristotelian logic, is a loose name for an approach to formal logic that began with Aristotle and was developed further in ancient history mostly by his followers, the Peripatetics. It was revived after the third century CE by Porphyry's Isagoge. Term logic revived in medieval times, first in Islamic logic by Alpharabius in the tenth century, and later in Christian Europe in the twelfth century with the advent of new logic, remaining dominant until the advent of predicate logic in the late nineteenth century. However, even if eclipsed by newer logical systems, term logic still plays a significant role in the study of logic. Rather than radically breaking with term logic, modern logics typically expand it. Aristotle's system Aristotle's logical work is collected in the six texts that are collectively known as the '' Organon''. Two of these texts in particular, namely th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Immediate Inference
An immediate inference is an inference which can be made from only one statement or proposition. For instance, from the statement "All toads are green", the immediate inference can be made that "no toads are not green" or "no toads are non-green" (Obverse). There are a number of ''immediate inferences'' which can validly be made using logical operations. There are also invalid immediate inferences which are syllogistic fallacies. Valid immediate inferences Converse *Given a type E statement, "No ''S'' are ''P''.", one can make the ''immediate inference'' that "No ''P'' are ''S''" which is the converse of the given statement. *Given a type I statement, "Some ''S'' are ''P''.", one can make the ''immediate inference'' that "Some ''P'' are ''S''" which is the converse of the given statement. Obverse *Given a type A statement, "All ''S'' are ''P''.", one can make the ''immediate inference'' that "No ''S'' are ''non-P''" which is the obverse of the given statement. *Given a t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Transposition (logic)
In logic and mathematics, contraposition, or ''transposition'', refers to the inference of going from a conditional statement into its logically equivalent contrapositive, and an associated proof method known as . The contrapositive of a statement has its antecedent and consequent negated and swapped. Conditional statement P \rightarrow Q. In formulas: the contrapositive of P \rightarrow Q is \neg Q \rightarrow \neg P . If ''P'', Then ''Q''. — If not ''Q'', Then not ''P''. "If ''it is raining,'' then ''I wear my coat''." — "If ''I don't wear my coat,'' then ''it isn't raining''." The law of contraposition says that a conditional statement is true if, and only if, its contrapositive is true. Contraposition ( \neg Q \rightarrow \neg P ) can be compared with three other operations: ; Inversion (the inverse), \neg P \rightarrow \neg Q:"If ''it is not raining,'' then ''I don't wear my coat''." Unlike the contrapositive, the inverse's truth value is not at all dependen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Conversion (logic)
In logic and mathematics, the converse of a categorical or implicational statement is the result of reversing its two constituent statements. For the implication ''P'' → ''Q'', the converse is ''Q'' → ''P''. For the categorical proposition ''All S are P'', the converse is ''All P are S''. Either way, the truth of the converse is generally independent from that of the original statement.Robert Audi, ed. (1999), ''The Cambridge Dictionary of Philosophy'', 2nd ed., Cambridge University Press: "converse". Implicational converse Let ''S'' be a statement of the form ''P implies Q'' (''P'' → ''Q''). Then the ''converse'' of ''S'' is the statement ''Q implies P'' (''Q'' → ''P''). In general, the truth of ''S'' says nothing about the truth of its converse, unless the antecedent ''P'' and the consequent ''Q'' are logically equivalent. For example, consider the true statement "If I am a human, then I am mortal." The converse of that statement is "If I am mortal, then I am a huma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Contraposition
In logic and mathematics, contraposition, or ''transposition'', refers to the inference of going from a conditional statement into its logically equivalent contrapositive, and an associated proof method known as . The contrapositive of a statement has its antecedent and consequent negated and swapped. Conditional statement P \rightarrow Q. In formulas: the contrapositive of P \rightarrow Q is \neg Q \rightarrow \neg P . If ''P'', Then ''Q''. — If not ''Q'', Then not ''P''. "If ''it is raining,'' then ''I wear my coat''." — "If ''I don't wear my coat,'' then ''it isn't raining''." The law of contraposition says that a conditional statement is true if, and only if, its contrapositive is true. Contraposition ( \neg Q \rightarrow \neg P ) can be compared with three other operations: ; Inversion (the inverse), \neg P \rightarrow \neg Q:"If ''it is not raining,'' then ''I don't wear my coat''." Unlike the contrapositive, the inverse's truth value is not at all dependen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Aristotelian Logic
In logic and formal semantics, term logic, also known as traditional logic, syllogistic logic or Aristotelian logic, is a loose name for an approach to formal logic that began with Aristotle and was developed further in ancient history mostly by his followers, the Peripatetics. It was revived after the third century CE by Porphyry's Isagoge. Term logic revived in medieval times, first in Islamic logic by Alpharabius in the tenth century, and later in Christian Europe in the twelfth century with the advent of new logic, remaining dominant until the advent of predicate logic in the late nineteenth century. However, even if eclipsed by newer logical systems, term logic still plays a significant role in the study of logic. Rather than radically breaking with term logic, modern logics typically expand it. Aristotle's system Aristotle's logical work is collected in the six texts that are collectively known as the '' Organon''. Two of these texts in particular, namely ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Term Logic
In logic and formal semantics, term logic, also known as traditional logic, syllogistic logic or Aristotelian logic, is a loose name for an approach to formal logic that began with Aristotle and was developed further in ancient history mostly by his followers, the Peripatetics. It was revived after the third century CE by Porphyry's Isagoge. Term logic revived in medieval times, first in Islamic logic by Alpharabius in the tenth century, and later in Christian Europe in the twelfth century with the advent of new logic, remaining dominant until the advent of predicate logic in the late nineteenth century. However, even if eclipsed by newer logical systems, term logic still plays a significant role in the study of logic. Rather than radically breaking with term logic, modern logics typically expand it. Aristotle's system Aristotle's logical work is collected in the six texts that are collectively known as the '' Organon''. Two of these texts in particular, namely th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
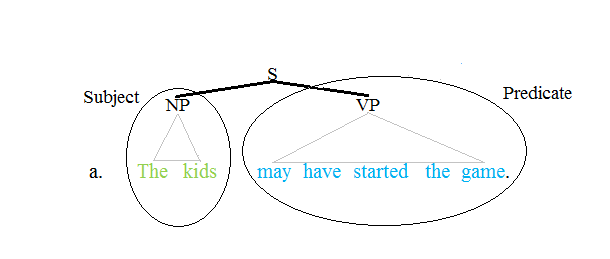
Predicate (grammar)
The term predicate is used in two ways in linguistics and its subfields. The first defines a predicate as everything in a standard declarative sentence except the subject (grammar), subject, and the other defines it as only the main content verb or associated predicative expression of a clause. Thus, by the first definition, the predicate of the sentence ''Frank likes cake'' is ''likes cake'', while by the second definition, it is only the content verb ''likes'', and ''Frank'' and ''cake'' are the argument (linguistics), arguments of this predicate. The conflict between these two definitions can lead to confusion. Syntax Traditional grammar The notion of a predicate in traditional grammar traces back to Aristotelian logic. A predicate is seen as a property that a subject has or is characterized by. A predicate is therefore an expression that can be ''true of'' something. Thus, the expression "is moving" is true of anything that is moving. This classical understanding of pred ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Negated
In logic, negation, also called the logical not or logical complement, is an operation that takes a proposition P to another proposition "not P", written \neg P, \mathord P, P^\prime or \overline. It is interpreted intuitively as being true when P is false, and false when P is true. For example, if P is "Spot runs", then "not P" is "Spot does not run". An operand of a negation is called a ''negand'' or ''negatum''. Negation is a unary logical connective. It may furthermore be applied not only to propositions, but also to notions, truth values, or semantic values more generally. In classical logic, negation is normally identified with the truth function that takes ''truth'' to ''falsity'' (and vice versa). In intuitionistic logic, according to the Brouwer–Heyting–Kolmogorov interpretation, the negation of a proposition P is the proposition whose proofs are the refutations of P. Definition ''Classical negation'' is an operation on one logical value, typically the value ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Subject (grammar)
A subject is one of the two main parts of a Sentence (linguistics), sentence (the other being the Predicate (grammar), predicate, which modifies the subject). For the simple Sentence (linguistics), sentence ''John runs'', ''John'' is the subject, a person or thing about whom the statement is made. Traditionally the subject is the word or phrase which controls the verb in the clause, that is to say with which the verb Agreement (linguistics), agrees (''John is'' but ''John and Mary are''). If there is no verb, as in ''Nicola what an idiot!'', or if the verb has a different subject, as in ''John I can't stand him!'', then 'John' is not considered to be the grammatical subject, but can be described as the ''Topic and comment, topic'' of the sentence. While these definitions apply to simple English sentences, defining the subject is more difficult in more complex sentences and languages. For example, in the sentence ''It is difficult to learn French'', the subject seems to be the wor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Square Of Opposition
In term logic (a branch of philosophical logic), the square of opposition is a diagram representing the relations between the four basic categorical propositions. The origin of the square can be traced back to Aristotle's tractate '' On Interpretation'' and its distinction between two oppositions: contradiction and contrariety. However, Aristotle did not draw any diagram; this was done several centuries later by Boethius. Summary In traditional logic, a proposition (Latin: ''propositio'') is a spoken assertion (''oratio enunciativa''), not the meaning of an assertion, as in modern philosophy of language and logic. A ''categorical proposition'' is a simple proposition containing two terms, subject () and predicate (), in which the predicate is either asserted or denied of the subject. Every categorical proposition can be reduced to one of four logical forms, named , , , and based on the Latin ' (I affirm), for the affirmative propositions and , and ' (I deny), for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |