|
Nonparametric
Nonparametric statistics is the branch of statistics that is not based solely on parametrized families of probability distributions (common examples of parameters are the mean and variance). Nonparametric statistics is based on either being distribution-free or having a specified distribution but with the distribution's parameters unspecified. Nonparametric statistics includes both descriptive statistics and statistical inference. Nonparametric tests are often used when the assumptions of parametric tests are violated. Definitions The term "nonparametric statistics" has been imprecisely defined in the following two ways, among others: Applications and purpose Non-parametric methods are widely used for studying populations that take on a ranked order (such as movie reviews receiving one to four stars). The use of non-parametric methods may be necessary when data have a ranking but no clear numerical interpretation, such as when assessing preferences. In terms of levels of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet Process
In probability theory, Dirichlet processes (after the distribution associated with Peter Gustav Lejeune Dirichlet) are a family of stochastic processes whose realizations are probability distributions. In other words, a Dirichlet process is a probability distribution whose range is itself a set of probability distributions. It is often used in Bayesian inference to describe the prior knowledge about the distribution of random variables—how likely it is that the random variables are distributed according to one or another particular distribution. As an example, a bag of 100 real-world dice is a ''random probability mass function (random pmf)'' - to sample this random pmf you put your hand in the bag and draw out a die, that is, you draw a pmf. A bag of dice manufactured using a crude process 100 years ago will likely have probabilities that deviate wildly from the uniform pmf, whereas a bag of state-of-the-art dice used by Las Vegas casinos may have barely perceptible imperfe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semiparametric Regression
In statistics, semiparametric regression includes regression models that combine parametric and nonparametric models. They are often used in situations where the fully nonparametric model may not perform well or when the researcher wants to use a parametric model but the functional form with respect to a subset of the regressors or the density of the errors is not known. Semiparametric regression models are a particular type of semiparametric modelling and, since semiparametric models contain a parametric component, they rely on parametric assumptions and may be misspecified and inconsistent, just like a fully parametric model. Methods Many different semiparametric regression methods have been proposed and developed. The most popular methods are the partially linear, index and varying coefficient models. Partially linear models A partially linear model is given by : Y_i = X'_i \beta + g\left(Z_i \right) + u_i, \, \quad i = 1,\ldots,n, \, where Y_ is the dependent v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonparametric Regression
Nonparametric regression is a category of regression analysis in which the predictor does not take a predetermined form but is constructed according to information derived from the data. That is, no parametric form is assumed for the relationship between predictors and dependent variable. Nonparametric regression requires larger sample sizes than regression based on parametric models because the data must supply the model structure as well as the model estimates. Definition In nonparametric regression, we have random variables X and Y and assume the following relationship: : \mathbb \mid X=x= m(x), where m(x) is some deterministic function. Linear regression is a restricted case of nonparametric regression where m(x) is assumed to be affine. Some authors use a slightly stronger assumption of additive noise: : Y = m(X) + U, where the random variable U is the `noise term', with mean 0. Without the assumption that m belongs to a specific parametric family of functions it is impo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonparametric Regression
Nonparametric regression is a category of regression analysis in which the predictor does not take a predetermined form but is constructed according to information derived from the data. That is, no parametric form is assumed for the relationship between predictors and dependent variable. Nonparametric regression requires larger sample sizes than regression based on parametric models because the data must supply the model structure as well as the model estimates. Definition In nonparametric regression, we have random variables X and Y and assume the following relationship: : \mathbb \mid X=x= m(x), where m(x) is some deterministic function. Linear regression is a restricted case of nonparametric regression where m(x) is assumed to be affine. Some authors use a slightly stronger assumption of additive noise: : Y = m(X) + U, where the random variable U is the `noise term', with mean 0. Without the assumption that m belongs to a specific parametric family of functions it is impo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel (statistics)
The term kernel is used in statistical analysis to refer to a window function. The term "kernel" has several distinct meanings in different branches of statistics. Bayesian statistics In statistics, especially in Bayesian statistics, the kernel of a probability density function (pdf) or probability mass function (pmf) is the form of the pdf or pmf in which any factors that are not functions of any of the variables in the domain are omitted. Note that such factors may well be functions of the parameters of the pdf or pmf. These factors form part of the normalization factor of the probability distribution, and are unnecessary in many situations. For example, in pseudo-random number sampling, most sampling algorithms ignore the normalization factor. In addition, in Bayesian analysis of conjugate prior distributions, the normalization factors are generally ignored during the calculations, and only the kernel considered. At the end, the form of the kernel is examined, and if it m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Data Envelopment Analysis
Data envelopment analysis (DEA) is a nonparametric method in operations research and economics for the estimation of production frontiers.Charnes et al (1978) DEA has been applied in a large range of fields including international banking, economic sustainability, police department operations, and logistical applicationsCharnes et al (1995) Emrouznejad et al (2016)Thanassoulis (1995) Additionally, DEA has been used to assess the performance of natural language processing models, and it has found other applications within machine learning.Zhou et al (2022)Guerrero et al (2022) Description DEA is used to empirically measure productive efficiency of decision-making units (DMUs). Although DEA has a strong link to production theory in economics, the method is also used for benchmarking in operations management, whereby a set of measures is selected to benchmark the performance of manufacturing and service operations. In benchmarking, the efficient DMUs, as defined by DEA, may not neces ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
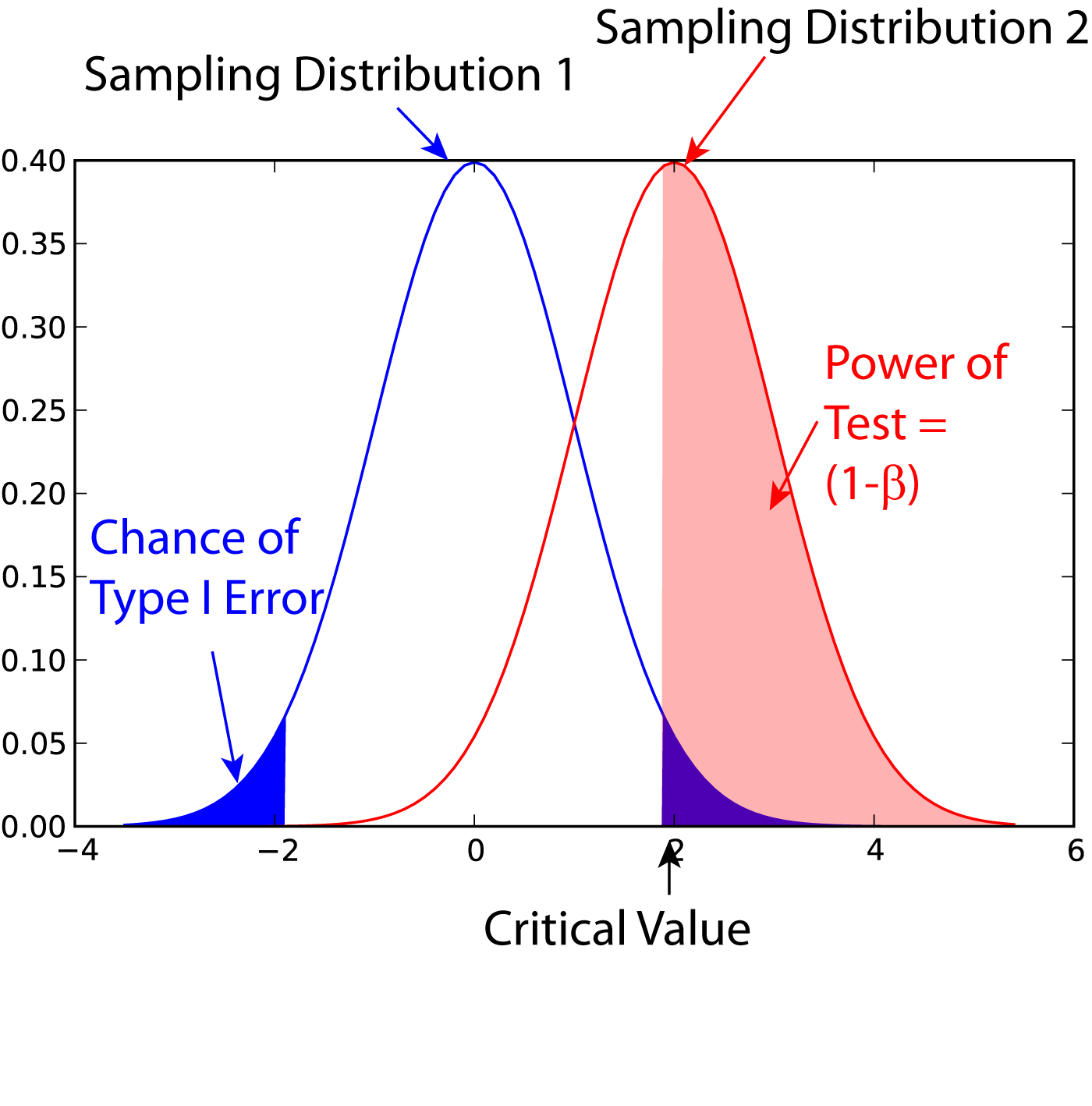
Statistical Power
In statistics, the power of a binary hypothesis test is the probability that the test correctly rejects the null hypothesis (H_0) when a specific alternative hypothesis (H_1) is true. It is commonly denoted by 1-\beta, and represents the chances of a true positive detection conditional on the actual existence of an effect to detect. Statistical power ranges from 0 to 1, and as the power of a test increases, the probability \beta of making a type II error by wrongly failing to reject the null hypothesis decreases. Notation This article uses the following notation: * ''β'' = probability of a Type II error, known as a "false negative" * 1 − ''β'' = probability of a "true positive", i.e., correctly rejecting the null hypothesis. "1 − ''β''" is also known as the power of the test. * ''α'' = probability of a Type I error, known as a "false positive" * 1 − ''α'' = probability of a "true negative", i.e., correctly not rejecting the null hypothesis Description For a ty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robust Statistics
Robust statistics are statistics with good performance for data drawn from a wide range of probability distributions, especially for distributions that are not normal. Robust statistical methods have been developed for many common problems, such as estimating location, scale, and regression parameters. One motivation is to produce statistical methods that are not unduly affected by outliers. Another motivation is to provide methods with good performance when there are small departures from a parametric distribution. For example, robust methods work well for mixtures of two normal distributions with different standard deviations; under this model, non-robust methods like a t-test work poorly. Introduction Robust statistics seek to provide methods that emulate popular statistical methods, but which are not unduly affected by outliers or other small departures from Statistical assumption, model assumptions. In statistics, classical estimation methods rely heavily on assumpti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-nearest Neighbors Algorithm
In statistics, the ''k''-nearest neighbors algorithm (''k''-NN) is a non-parametric supervised learning method first developed by Evelyn Fix and Joseph Hodges in 1951, and later expanded by Thomas Cover. It is used for classification and regression. In both cases, the input consists of the ''k'' closest training examples in a data set. The output depends on whether ''k''-NN is used for classification or regression: :* In ''k-NN classification'', the output is a class membership. An object is classified by a plurality vote of its neighbors, with the object being assigned to the class most common among its ''k'' nearest neighbors (''k'' is a positive integer, typically small). If ''k'' = 1, then the object is simply assigned to the class of that single nearest neighbor. :* In ''k-NN regression'', the output is the property value for the object. This value is the average of the values of ''k'' nearest neighbors. If ''k'' = 1, then the output is simply assigned to the v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Descriptive Statistics
A descriptive statistic (in the count noun sense) is a summary statistic that quantitatively describes or summarizes features from a collection of information, while descriptive statistics (in the mass noun sense) is the process of using and analysing those statistics. Descriptive statistic is distinguished from inferential statistics (or inductive statistics) by its aim to summarize a sample, rather than use the data to learn about the population that the sample of data is thought to represent. This generally means that descriptive statistics, unlike inferential statistics, is not developed on the basis of probability theory, and are frequently nonparametric statistics. Even when a data analysis draws its main conclusions using inferential statistics, descriptive statistics are generally also presented. For example, in papers reporting on human subjects, typically a table is included giving the overall sample size, sample sizes in important subgroups (e.g., for each treatment or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Statistics
Parametric statistics is a branch of statistics which assumes that sample data comes from a population that can be adequately modeled by a probability distribution that has a fixed set of Statistical parameter, parameters. Conversely a non-parametric model does not assume an explicit (finite-parametric) mathematical form for the distribution when modeling the data. However, it may make some assumptions about that distribution, such as continuity or symmetry. Most well-known statistical methods are parametric. Regarding nonparametric (and semiparametric) models, David Cox (statistician), Sir David Cox has said, "These typically involve fewer assumptions of structure and distributional form but usually contain strong assumptions about independencies". Example The normal distribution, normal family of distributions all have the same general shape and are ''parameterized'' by mean and standard deviation. That means that if the mean and standard deviation are known and if the distribu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |