|
Non Ideal Compressible Fluid Dynamics
Non ideal compressible fluid dynamics (NICFD), or non ideal Compressible flow, gas dynamics, is a branch of fluid mechanics studying the dynamic behavior of fluids not obeying Ideal gas, ideal-gas thermodynamics. It is for example the case of dense vapors, Supercritical fluid, supercritical flows and compressible two-phase flows. With the term dense vapors, we indicate all fluids in the Gas, gaseous state characterized by thermodynamic conditions close to saturation and the Critical point (thermodynamics), critical point. Supercritical fluids feature instead values of pressure and temperature larger than their critical values, whereas two-phase flows are characterized by the simultaneous presence of both liquid and gas phases. In all these cases, the fluid requires to be modelled as a real gas, since its thermodynamic behavior considerably differs from that of an ideal gas, which by contrast appears for dilute thermodynamic conditions. The ideal-gas law can be employed in general as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Volume
In thermodynamics, the specific volume of a substance (symbol: , nu) is an intrinsic property of the substance, defined as the ratio of the substance's volume () to its mass (). It is the reciprocal of density (rho) and it is related to the molar volume and molar mass: :\nu = \frac = \rho^ = \frac The standard unit of specific volume is cubic meters per kilogram (m3/kg), but other units include ft3/lb, ft3/slug, or mL/g. Specific volume for an ideal gas is related to the molar gas constant () and the gas's temperature (), pressure (), and molar mass () as shown: Since PV = and n = \frac : \nu = \frac = \frac Applications Specific volume is commonly applied to: * Molar volume * Volume (thermodynamics) * Partial molar volume Imagine a variable-volume, airtight chamber containing a certain number of atoms of oxygen gas. Consider the following four examples: * If the chamber is made smaller without allowing gas in or out, the density increases and the specific volume dec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
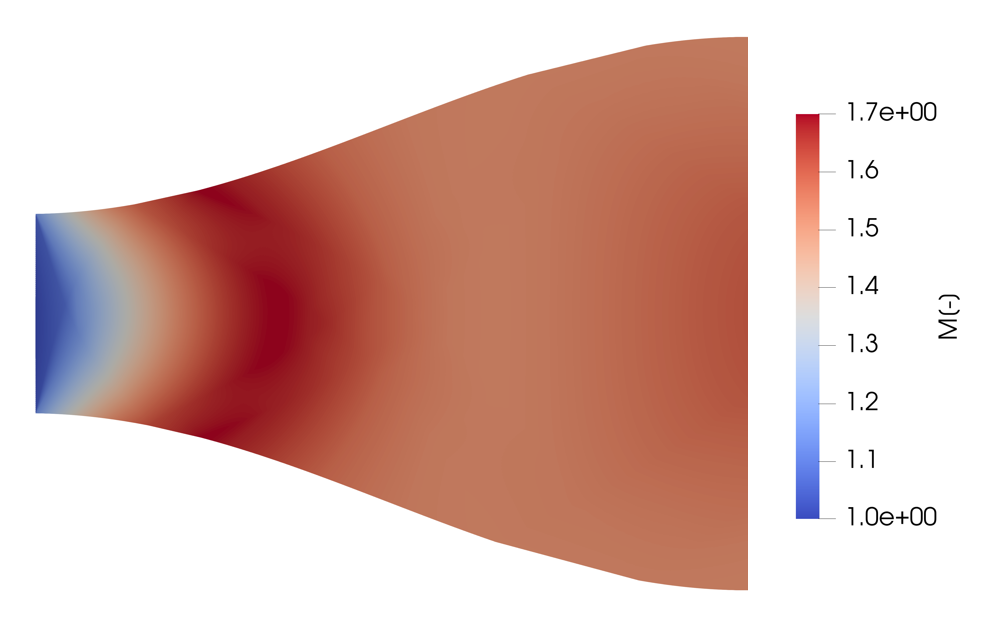
Mach Number
Mach number (M or Ma) (; ) is a dimensionless quantity in fluid dynamics representing the ratio of flow velocity past a boundary to the local speed of sound. It is named after the Moravian physicist and philosopher Ernst Mach. : \mathrm = \frac, where: : is the local Mach number, : is the local flow velocity with respect to the boundaries (either internal, such as an object immersed in the flow, or external, like a channel), and : is the speed of sound in the medium, which in air varies with the square root of the thermodynamic temperature. By definition, at Mach1, the local flow velocity is equal to the speed of sound. At Mach0.65, is 65% of the speed of sound (subsonic), and, at Mach1.35, is 35% faster than the speed of sound (supersonic). Pilots of high-altitude aerospace vehicles use flight Mach number to express a vehicle's true airspeed, but the flow field around a vehicle varies in three dimensions, with corresponding variations in local Mach number. The loc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stagnation Point
In fluid dynamics, a stagnation point is a point in a flow field where the local velocity Velocity is the directional speed of an object in motion as an indication of its rate of change in position as observed from a particular frame of reference and as measured by a particular standard of time (e.g. northbound). Velocity i ... of the fluid is zero.Clancy, L.J. (1975), ''Aerodynamics'', Pitman Publishing Limited, London. A plentiful, albeit surprising, example of such points seem to appear in all but the most extreme cases of fluid dynamics in the form of the " No-slip condition"; the assumption that any portion of a flow field lying along some boundary consists of nothing but stagnation points (the question as to whether this assumption reflects reality or is simply a mathematical convenience has been a continuous subject of debate since the principle was first established). The Bernoulli equation shows that the static pressure is highest when the velocity is zer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Heat Capacity
In thermodynamics, the specific heat capacity (symbol ) of a substance is the heat capacity of a sample of the substance divided by the mass of the sample, also sometimes referred to as massic heat capacity. Informally, it is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. The SI unit of specific heat capacity is joule per kelvin per kilogram, J⋅kg−1⋅K−1. For example, the heat required to raise the temperature of of water by is , so the specific heat capacity of water is . Specific heat capacity often varies with temperature, and is different for each state of matter. Liquid water has one of the highest specific heat capacities among common substances, about at 20 °C; but that of ice, just below 0 °C, is only . The specific heat capacities of iron, granite, and hydrogen gas are about 449 J⋅kg−1⋅K−1, 790 J⋅kg−1⋅K−1, and 14300 J⋅kg−1⋅K−1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Capacity Ratio
In thermal physics and thermodynamics, the heat capacity ratio, also known as the adiabatic index, the ratio of specific heats, or Laplace's coefficient, is the ratio of the heat capacity at constant pressure () to heat capacity at constant volume (). It is sometimes also known as the '' isentropic expansion factor'' and is denoted by ( gamma) for an ideal gasγ first appeared in an article by the French mathematician, engineer, and physicist Siméon Denis Poisson: * On p. 332, Poisson defines γ merely as a small deviation from equilibrium which causes small variations of the equilibrium value of the density ρ. In Poisson's article of 1823 – * γ was expressed as a function of density D (p. 8) or of pressure P (p. 9). Meanwhile, in 1816 the French mathematician and physicist Pierre-Simon Laplace had found that the speed of sound depends on the ratio of the specific heats. * However, he didn't denote the ratio as γ. In 1825, Laplace stated that the speed of soun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pressure–volume Diagram
A pressure–volume diagram (or PV diagram, or volume–pressure loop) is used to describe corresponding changes in volume and pressure in a system. They are commonly used in thermodynamics, cardiovascular physiology, and respiratory physiology. PV diagrams, originally called indicator diagrams, were developed in the 18th century as tools for understanding the efficiency of steam engines. Description A PV diagram plots the change in pressure ''P'' with respect to volume ''V'' for some process or processes. Typically in thermodynamics, the set of processes forms a cycle, so that upon completion of the cycle there has been no net change in state of the system; i.e. the device returns to the starting pressure and volume. The figure shows the features of an idealized PV diagram. It shows a series of numbered states (1 through 4). The path between each state consists of some process (A through D) which alters the pressure or volume of the system (or both). A key feature of the di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isentropic Process
In thermodynamics, an isentropic process is an idealized thermodynamic process that is both adiabatic and reversible. The work transfers of the system are frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes. This process is idealized because reversible processes do not occur in reality; thinking of a process as both adiabatic and reversible would show that the initial and final entropies are the same, thus, the reason it is called isentropic (entropy does not change). Thermodynamic processes are named based on the effect they would have on the system (ex. isovolumetric: constant volume, isenthalpic: constant enthalpy). Even though in reality it is not necessarily possible to carry out an isentropic process, some may be approximated as such. The word "isentropic" can be interpreted in another way, since its meaning is deducible from its etymology. It means a p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change, and information systems including the transmission of information in telecommunication. The thermodynamic concept was referred to by Scottish scientist and engineer William Rankine in 1850 with the names ''thermodynamic function'' and ''heat-potential''. In 1865, German physicist Rudolf Clausius, one of the leading founders of the field of thermodynamics, defined it as the quotient of an infinitesimal amount ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landau Derivative
In gas dynamics, the Landau derivative or fundamental derivative of gas dynamics, named after Lev Landau who introduced it in 1942, refers to a dimensionless physical quantity characterizing the curvature of the isentrope drawn on the specific volume versus pressure plane. Specifically, the Landau derivative is a second derivative of specific volume with respect to pressure. The derivative is denoted commonly using the symbol \Gamma or \alpha and is defined byLandau, L. D., & Lifshitz, E. M. (2013). Fluid mechanics: Landau And Lifshitz: course of theoretical physics, Volume 6 (Vol. 6). Elsevier.Lambrakis, K. C., & Thompson, P. A. (1972). Existence of real fluids with a negative fundamental derivative Γ. Physics of Fluids, 15(5), 933-935. \Gamma = \frac\left(\frac\right)_s where * c is the sound speed, * \upsilon = 1/\rho is the specific volume, * \rho is the density, * p is the pressure, and * s is the specific entropy. Alternate representations of \Gamma include \begin \Gam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peng-Robinson Equation
Cubic equations of state are a specific class of thermodynamic models for modeling the pressure of a gas as a function of temperature and density and which can be rewritten as a cubic function of the molar volume. Equations of state are generally applied in the fields of physical chemistry and chemical engineering, particularly in the modeling of vapor–liquid equilibrium and chemical engineering process design. Van der Waals equation of state The van der Waals equation of state may be written as : \left(p + \frac\right)\left(V_\text - b\right) = RT where T is the absolute temperature, p is the pressure, V_\text is the molar volume and R is the universal gas constant. Note that V_\text = V / n, where V is the volume, and n=N/N_\text, where n is the number of moles, N is the number of particles, and N_\text is the Avogadro constant. These definitions apply to all equations of state below as well. The substance-specific constants a and b can be calculated from the critical pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Van Der Waals Equation
In chemistry and thermodynamics, the Van der Waals equation (or Van der Waals equation of state) is an equation of state which extends the ideal gas law to include the effects of interaction between molecules of a gas, as well as accounting for the finite size of the molecules. The ideal gas law treats gas molecules as point particles that interact with their containers but not each other, meaning they neither take up space nor change kinetic energy during collisions (i.e. all collisions are perfectly elastic). The ideal gas law states that the volume ''V'' occupied by ''n'' moles of any gas has a pressure ''P'' at temperature ''T'' given by the following relationship, where ''R'' is the gas constant: :PV=nRT To account for the volume occupied by real gas molecules, the Van der Waals equation replaces V/n in the ideal gas law with (V_m-b), where ''Vm'' is the molar volume of the gas and ''b'' is the volume occupied by the molecules of one mole: :P(V_m - b)=R T The second ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg)


