|
Narrow Class Group
In algebraic number theory, the narrow class group of a number field ''K'' is a refinement of the class group of ''K'' that takes into account some information about embeddings of ''K'' into the field of real numbers. Formal definition Suppose that ''K'' is a finite extension of Q. Recall that the ordinary class group of ''K'' is defined as the quotient :C_K = I_K / P_K,\,\! where ''I''''K'' is the group of fractional ideals of ''K'', and ''P''''K'' is the subgroup of principal fractional ideals of ''K'', that is, ideals of the form ''aO''''K'' where ''a'' is an element of ''K''. The narrow class group is defined to be the quotient :C_K^+ = I_K / P_K^+, where now ''P''''K''+ is the group of totally positive principal fractional ideals of ''K''; that is, ideals of the form ''aO''''K'' where ''a'' is an element of ''K'' such that σ(''a'') is ''positive'' for every embedding :\sigma : K \to \mathbb. Uses The narrow class group features prominently in the theory of repre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Number Theory
Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic objects such as algebraic number fields and their rings of integers, finite fields, and Algebraic function field, function fields. These properties, such as whether a ring (mathematics), ring admits unique factorization, the behavior of ideal (ring theory), ideals, and the Galois groups of field (mathematics), fields, can resolve questions of primary importance in number theory, like the existence of solutions to Diophantine equations. History Diophantus The beginnings of algebraic number theory can be traced to Diophantine equations, named after the 3rd-century Alexandrian mathematician, Diophantus, who studied them and developed methods for the solution of some kinds of Diophantine equations. A typical Diophantine problem is to find two in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field Norm
In mathematics, the (field) norm is a particular mapping defined in field theory, which maps elements of a larger field into a subfield. Formal definition Let ''K'' be a field and ''L'' a finite extension (and hence an algebraic extension) of ''K''. The field ''L'' is then a finite-dimensional vector space over ''K''. Multiplication by ''α'', an element of ''L'', :m_\alpha\colon L\to L :m_\alpha (x) = \alpha x, is a ''K''-linear transformation of this vector space into itself. The norm, N''L''/''K''(''α''), is defined as the determinant of this linear transformation. If ''L''/''K'' is a Galois extension, one may compute the norm of ''α'' ∈ ''L'' as the product of all the Galois conjugates of ''α'': :\operatorname_(\alpha)=\prod_ \sigma(\alpha), where Gal(''L''/''K'') denotes the Galois group of ''L''/''K''. (Note that there may be a repetition in the terms of the product.) For a general field extension ''L''/''K'', and nonzero ''α'' in ''L'', let ''σ''(''α ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Class Group
In mathematics, the ideal class group (or class group) of an algebraic number field K is the quotient group J_K/P_K where J_K is the group of fractional ideals of the ring of integers of K, and P_K is its subgroup of principal ideals. The class group is a measure of the extent to which unique factorization fails in the ring of integers of K. The order of the group, which is finite, is called the class number of K. The theory extends to Dedekind domains and their fields of fractions, for which the multiplicative properties are intimately tied to the structure of the class group. For example, the class group of a Dedekind domain is trivial if and only if the ring is a unique factorization domain. History and origin of the ideal class group Ideal class groups (or, rather, what were effectively ideal class groups) were studied some time before the idea of an ideal was formulated. These groups appeared in the theory of quadratic forms: in the case of binary integral quadra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Order Of A Group
In mathematics, the order of a finite group is the number of its elements. If a group is not finite, one says that its order is ''infinite''. The ''order'' of an element of a group (also called period length or period) is the order of the subgroup generated by the element. If the group operation is denoted as a multiplication, the order of an element of a group, is thus the smallest positive integer such that , where denotes the identity element of the group, and denotes the product of copies of . If no such exists, the order of is infinite. The order of a group is denoted by or , and the order of an element is denoted by or , instead of \operatorname(\langle a\rangle), where the brackets denote the generated group. Lagrange's theorem states that for any subgroup of a finite group , the order of the subgroup divides the order of the group; that is, is a divisor of . In particular, the order of any element is a divisor of . Example The symmetric group S3 has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Class Group
In mathematics, the ideal class group (or class group) of an algebraic number field K is the quotient group J_K/P_K where J_K is the group of fractional ideals of the ring of integers of K, and P_K is its subgroup of principal ideals. The class group is a measure of the extent to which unique factorization fails in the ring of integers of K. The order of the group, which is finite, is called the class number of K. The theory extends to Dedekind domains and their fields of fractions, for which the multiplicative properties are intimately tied to the structure of the class group. For example, the class group of a Dedekind domain is trivial if and only if the ring is a unique factorization domain. History and origin of the ideal class group Ideal class groups (or, rather, what were effectively ideal class groups) were studied some time before the idea of an ideal was formulated. These groups appeared in the theory of quadratic forms: in the case of binary integr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
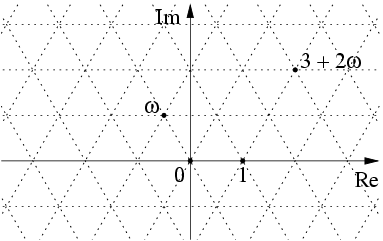
Eisenstein Prime
In mathematics, the Eisenstein integers (named after Gotthold Eisenstein), occasionally also known as Eulerian integers (after Leonhard Euler), are the complex numbers of the form : z = a + b\omega , where and are integers and : \omega = \frac = e^ is a primitive (hence non-real) cube root of unity. The Eisenstein integers form a triangular lattice in the complex plane, in contrast with the Gaussian integers, which form a square lattice in the complex plane. The Eisenstein integers are a countably infinite set. Properties The Eisenstein integers form a commutative ring of algebraic integers in the algebraic number field – the third cyclotomic field. To see that the Eisenstein integers are algebraic integers note that each is a root of the monic polynomial : z^2 - (2a - b)\;\!z + \left(a^2 - ab + b^2\right)~. In particular, satisfies the equation : \omega^2 + \omega + 1 = 0~. The product of two Eisenstein integers and is given explicitly by : (a + b\;\!\omega) \;\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat's Theorem On Sums Of Two Squares
In additive number theory, Pierre de Fermat, Fermat's theorem on sums of two squares states that an Even and odd numbers, odd prime number, prime ''p'' can be expressed as: :p = x^2 + y^2, with ''x'' and ''y'' integers, if and only if :p \equiv 1 \pmod. The prime numbers for which this is true are called Pythagorean primes. For example, the primes 5, 13, 17, 29, 37 and 41 are all Modular_arithmetic#Congruence, congruent to 1 modular arithmetic, modulo 4, and they can be expressed as sums of two squares in the following ways: :5 = 1^2 + 2^2, \quad 13 = 2^2 + 3^2, \quad 17 = 1^2 + 4^2, \quad 29 = 2^2 + 5^2, \quad 37 = 1^2 + 6^2, \quad 41 = 4^2 + 5^2. On the other hand, the primes 3, 7, 11, 19, 23 and 31 are all congruent to 3 modulo 4, and none of them can be expressed as the sum of two squares. This is the easier part of the theorem, and follows immediately from the observation that all squares are congruent to 0 (if number squared is even) or 1 (if number squared is odd) modul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theorem
In mathematics and formal logic, a theorem is a statement (logic), statement that has been Mathematical proof, proven, or can be proven. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of the axioms and previously proved theorems. In mainstream mathematics, the axioms and the inference rules are commonly left implicit, and, in this case, they are almost always those of Zermelo–Fraenkel set theory with the axiom of choice (ZFC), or of a less powerful theory, such as Peano arithmetic. Generally, an assertion that is explicitly called a theorem is a proved result that is not an immediate consequence of other known theorems. Moreover, many authors qualify as ''theorems'' only the most important results, and use the terms ''lemma'', ''proposition'' and ''corollary'' for less important theorems. In mathematical logic, the concepts of theorems and proofs have been formal system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Field
In algebraic number theory, a quadratic field is an algebraic number field of Degree of a field extension, degree two over \mathbf, the rational numbers. Every such quadratic field is some \mathbf(\sqrt) where d is a (uniquely defined) square-free integer different from 0 and 1. If d>0, the corresponding quadratic field is called a real quadratic field, and, if d<0, it is called an imaginary quadratic field or a complex quadratic field, corresponding to whether or not it is a Field extension, subfield of the field of the real numbers. Quadratic fields have been studied in great depth, initially as part of the theory of binary quadratic forms. There remain some unsolved problems. The class number problem is particularly important. Ring of integers Discriminant For a nonzero square free integer , the Discriminant of an algebraic number field, discriminant of the quadratic field is |
Mathematical Proof
A mathematical proof is a deductive reasoning, deductive Argument-deduction-proof distinctions, argument for a Proposition, mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning that establish logical certainty, to be distinguished from empirical evidence, empirical arguments or non-exhaustive inductive reasoning that establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in ''all'' possible cases. A proposition that has not been proved but is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Legendre Symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo of an odd prime number ''p'': its value at a (nonzero) quadratic residue mod ''p'' is 1 and at a non-quadratic residue (''non-residue'') is −1. Its value at zero is 0. The Legendre symbol was introduced by Adrien-Marie Legendre in 1797 or 1798 in the course of his attempts at proving the law of quadratic reciprocity. Generalizations of the symbol include the Jacobi symbol and Dirichlet characters of higher order. The notational convenience of the Legendre symbol inspired introduction of several other "symbols" used in algebraic number theory, such as the Hilbert symbol and the Artin symbol. Definition Let p be an odd prime number. An integer a is a quadratic residue modulo p if it is modular arithmetic, congruent to a square number, perfect square modulo p and is a quadratic nonresidue modulo p otherwise. The Legendre symbol is a function of a a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant Of An Algebraic Number Field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the (ring of integers of the) algebraic number field. More specifically, it is proportional to the squared volume of the fundamental domain of the ring of integers, and it regulates which primes are ramified. The discriminant is one of the most basic invariants of a number field, and occurs in several important analytic formulas such as the functional equation of the Dedekind zeta function of K, and the analytic class number formula for K. A theorem of Hermite states that there are only finitely many number fields of bounded discriminant, however determining this quantity is still an open problem, and the subject of current research. The discriminant of K can be referred to as the absolute discriminant of K to distinguish it from the relative discriminant of an extension K/L of number fields. The latter is an ideal in the ring of integers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |