|
Mathethon
A Mathethon is a computational mathematics competition that is primarily focused on Computer-Based Math, computer-based math in contrast to math competitions that use scientific calculators or Handwriting, handwritten only. Mathethons are analogous to hackathons for computer programming competitions. They can very in academic difficulty from elementary competitions, middle school, high school, and college level mathematics. They can be held in person individually, as a group, or hosted virtually online.https://artofproblemsolving.com/wiki/index.php/List_of_United_States_high_school_mathematics_competitions?srsltid=AfmBOoq_1HMV9qU7y9QaHDm0EDNkjCM_tGkKWmdW5PAztz2eWO3mC5a6 Competition categories * Algorithm, Algorithmic problem solving * Biomathematics * Computational informatics * Computational physics * Computational mechanics#Mathematics, Computational mechanics * Computational science * Computational statistics * Cryptography * Data mining * Discrete mathematics * Machine lear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hackathon
A hackathon (also known as a hack day, hackfest, datathon or codefest; a portmanteau of '' hacking'' and ''marathon'') is an event where people engage in rapid and collaborative engineering over a relatively short period of time such as 24 or 48 hours. They are often run using agile software development practices, such as sprint-like design wherein computer programmers and others involved in software development, including graphic designers, interface designers, product managers, domain experts, and others collaborate intensively on engineering projects, such as software engineering. The goal of a hackathon is to create functioning software or hardware by the end of the event. Hackathons tend to have a specific focus, which can include the programming language used, the operating system, an application, an API, or the subject and the demographic group of the programmers. In other cases, there is no restriction on the type of software being created or the design of the new syst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
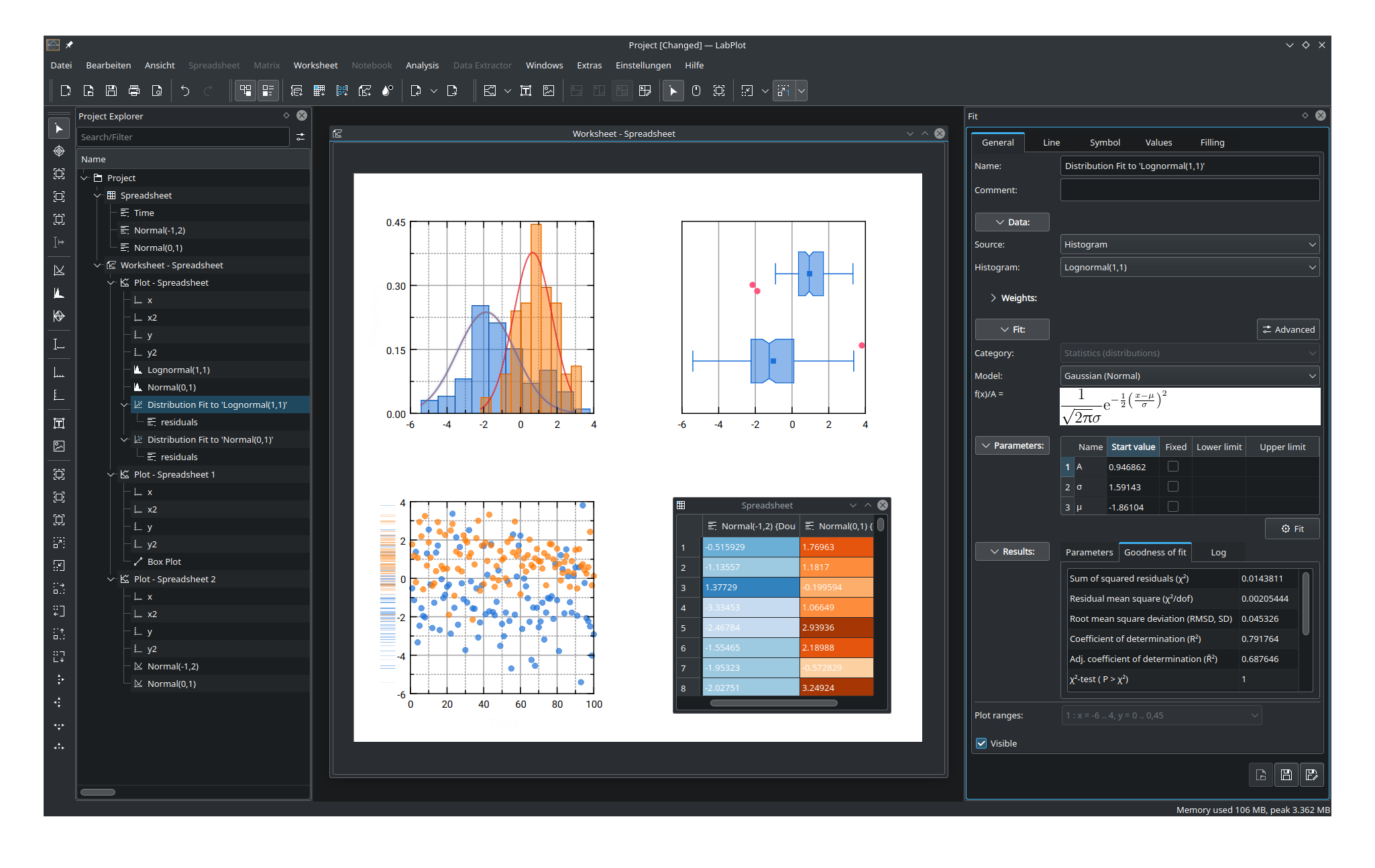
LabPlot 2
LabPlot is a free and open-source, cross-platform computer program for interactive scientific plotting, curve fitting, nonlinear regression, data processing and data analysis. LabPlot is available, under the GPL-2.0-or-later license, for Windows, macOS, Linux, FreeBSD and Haiku operating systems. It has a graphical user interface, a command-line interface, and an interactive and animated notebook interface. It is similar to Origin and able to import Origin's data files. Features include the Hilbert transform function, statistics, color maps, conditional formatting, and multi-axes. History In 2008, developers of LabPlot and SciDAVis (another Origin clone, forked from QtiPlot) "found their project goals to be very similar" and decided to merge their code into a common backend while maintaining two frontends: LabPlot, integrated with the KDE desktop environment (DE); and SciDAVis, written in DE-independent Qt with fewer dependencies for easier cross-platform use. Starting Apr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Mathematics
Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a way analogous to discrete variables, having a bijection with the set of natural numbers) rather than "continuous" (analogously to continuous functions). Objects studied in discrete mathematics include integers, Graph (discrete mathematics), graphs, and Statement (logic), statements in Mathematical logic, logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumeration, enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets (finite sets or sets with the same cardinality as the natural numbers). However, there is no exact definition of the term "discrete mathematics". The set of objects studied in discrete mathematics can be finite or infinite. The term finite mathematics is sometime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Visualization
Mathematics, Mathematical phenomena can be understood and explored via Visualization (graphic), visualization. Classically, this consisted of two-dimensional drawings or building three-dimensional models (particularly plaster models in the 19th and early 20th century). In contrast, today it most frequently consists of Scientific computing, using computers to make static two- or three-dimensional drawings, animations, or interactive programs. Writing programs to visualize mathematics is an aspect of computational geometry. Applications Mathematical visualization is used throughout mathematics, particularly in the fields of geometry and analysis. Notable examples include plane curves, space curves, polyhedra, ordinary differential equations, partial differential equations (particularly numerical solutions, as in fluid dynamics or minimal surfaces such as soap films), conformal maps, fractals, and Chaos theory, chaos. Geometry Geometry can be defined as the study of shapes their siz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Origami
) is the Japanese art of paper folding. In modern usage, the word "origami" is often used as an inclusive term for all folding practices, regardless of their culture of origin. The goal is to transform a flat square sheet of paper into a finished sculpture through folding and sculpting techniques. Modern origami practitioners generally discourage the use of cuts, glue, or markings on the paper. Origami folders often use the Japanese word ' to refer to designs which use cuts. In the detailed Japanese classification, origami is divided into stylized ceremonial origami (儀礼折り紙, ''girei origami'') and recreational origami (遊戯折り紙, ''yūgi origami''), and only recreational origami is generally recognized as origami. In Japan, ceremonial origami is generally called "origata" ( :ja:折形) to distinguish it from recreational origami. The term "origata" is one of the old terms for origami. The small number of basic origami folds can be combined in a variety of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics Of Paper Folding
The discipline of origami or paper folding has received a considerable amount of mathematical study. Fields of interest include a given paper model's flat-foldability (whether the model can be flattened without damaging it), and the use of paper folds to solve mathematical equations up to the third order. Computational origami is a recent branch of computer science that is concerned with studying algorithms that solve paper-folding problems. The field of computational origami has also grown significantly since its inception in the 1990s with Robert Lang's TreeMaker algorithm to assist in the precise folding of bases. Computational origami results either address origami design or origami foldability."Lecture: Recent Results in Computational Origami". ''Origami USA: We are the American national society devoted to origami, the art of paperfolding''. Retrieved 2022-05-08. In origami design problems, the goal is to design an object that can be folded out of paper given a specific targ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Chemistry
Mathematical chemistry is the area of research engaged in novel applications of mathematics to chemistry; it concerns itself principally with the mathematical modeling of chemical phenomena. Mathematical chemistry has also sometimes been called computer chemistry, but should not be confused with computational chemistry. Major areas of research in mathematical chemistry include chemical graph theory, which deals with topology such as the mathematical study of isomerism and the development of topological descriptors or indices which find application in quantitative structure-property relationships; and chemical aspects of group theory, which finds applications in stereochemistry and quantum chemistry. Another important area is molecular knot theory and circuit topology that describe the topology of folded linear molecules such as proteins and nucleic acids. The history of the approach may be traced back to the 19th century. Georg Helm published a treatise titled "The Principles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic computation, symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences like economics, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics (predicting the motions of planets, stars and galaxies), numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Simulation
Computer simulation is the running of a mathematical model on a computer, the model being designed to represent the behaviour of, or the outcome of, a real-world or physical system. The reliability of some mathematical models can be determined by comparing their results to the real-world outcomes they aim to predict. Computer simulations have become a useful tool for the mathematical modeling of many natural systems in physics (computational physics), astrophysics, climatology, chemistry, biology and manufacturing, as well as human systems in economics, psychology, social science, health care and engineering. Simulation of a system is represented as the running of the system's model. It can be used to explore and gain new insights into new technology and to estimate the performance of systems too complex for analytical solutions. Computer simulations are realized by running computer programs that can be either small, running almost instantly on small devices, or large-scale ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Model
A computational model uses computer programs to simulate and study complex systems using an algorithmic or mechanistic approach and is widely used in a diverse range of fields spanning from physics, engineering, chemistry and biology to economics, psychology, cognitive science and computer science. The system under study is often a complex nonlinear system for which simple, intuitive analytical solutions are not readily available. Rather than deriving a mathematical analytical solution to the problem, experimentation with the model is done by adjusting the parameters of the system in the computer, and studying the differences in the outcome of the experiments. Operation theories of the model can be derived/deduced from these computational experiments. Examples of common computational models are weather forecasting models, earth simulator models, flight simulator models, molecular protein folding models, Computational Engineering Models (CEM), and neural network models. Se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |