|
Linear Response Function
A linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response. Because of its many applications in information theory, physics and engineering there exist alternative names for specific linear response functions such as susceptibility, impulse response or impedance, see also transfer function. The concept of a Green's function or fundamental solution of an ordinary differential equation is closely related. Mathematical definition Denote the input of a system by h(t) (e.g. a force), and the response of the system by x(t) (e.g. a position). Generally, the value of x(t) will depend not only on the present value of h(t), but also on past values. Approximately x(t) is a weighted sum of the previous values of h(t'), with the weights given by the linear response function \chi(t-t'): x(t) = \int_^t dt'\, \chi(t-t') h(t') + \cdots\,. The explicit term on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Transducer
Signal transduction is the process by which a chemical or physical signal is transmitted through a cell as a biochemical cascade, series of molecular events, most commonly protein phosphorylation catalyzed by protein kinases, which ultimately results in a cellular response. Proteins responsible for detecting stimuli are generally termed receptor (biology), receptors, although in some cases the term sensor is used. The changes elicited by ligand binding (or signal sensing) in a receptor give rise to a biochemical cascade, which is a chain of biochemical events known as a Cell signaling#Signaling pathways, signaling pathway. When signaling pathways interact with one another they form networks, which allow cellular responses to be coordinated, often by combinatorial signaling events. At the molecular level, such responses include changes in the transcription (biology), transcription or translation (biology), translation of genes, and post-translational modification, post-translation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called ''analysis''. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term ''Fourier transform'' refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time. The Fourier transform of a function is a complex-valued function representing the complex sinusoids that comprise the original function. For each frequency, the magnitude ( absolute value) of the complex value represents the amplitude of a constituent complex sinusoid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interaction Picture
In quantum mechanics, the interaction picture (also known as the Dirac picture after Paul Dirac) is an intermediate representation between the Schrödinger picture and the Heisenberg picture. Whereas in the other two pictures either the state vector or the operators carry time dependence, in the interaction picture both carry part of the time dependence of observables. The interaction picture is useful in dealing with changes to the wave functions and observables due to interactions. Most field-theoretical calculations use the interaction representation because they construct the solution to the many-body Schrödinger equation as the solution to the free-particle problem plus some unknown interaction parts. Equations that include operators acting at different times, which hold in the interaction picture, don't necessarily hold in the Schrödinger or the Heisenberg picture. This is because time-dependent unitary transformations relate operators in one picture to the analogous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory. Group theory The commutator of two elements, and , of a group , is the element : . This element is equal to the group's identity if and only if and commute (from the definition , being equal to the identity if and only if ). The set of all commutators of a group is not in general closed under the group operation, but the subgroup of ''G'' generated by all commutators is closed and is called the ''derived group'' or the '' commutator subgroup'' of ''G''. Commutators are used to define nilpotent and solvable groups and the largest abelian quotient group. The definition of the commutator above is used throughout this article, but many other group theorists define the commutator as :. Identities (group theory) Commutator identities are an important tool in group theory. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Susceptibility (other)
Susceptibility may refer to: Physics and engineering In physics the susceptibility is a quantification for the change of an extensive property under variation of an intensive property. The word may refer to: * In physics, the susceptibility of a material or substance describes its response to an applied field. For example: ** Magnetic susceptibility ** Electric susceptibility * The two types of susceptibility above are examples of a linear response function; sometimes the terms ''susceptibility'' and ''linear response function'' are used interchangeably. *In electromagnetic compatibility (EMC), susceptibility is the sensitivity of a device's function to incoming electromagnetic interference Health and medicine * In epidemiology, a susceptible individual is a member of a population who is at risk of becoming infected by a disease * In microbiology, pharmacology, and medicine drug susceptibility is the ability of a microorganism to be inhibited or killed by the drug, as in ant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian Function
Hamiltonian mechanics emerged in 1833 as a reformulation of Lagrangian mechanics. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (generalized) ''momenta''. Both theories provide interpretations of classical mechanics and describe the same physical phenomena. Hamiltonian mechanics has a close relationship with geometry (notably, symplectic geometry and Poisson structures) and serves as a link between classical and quantum mechanics. Overview Phase space coordinates (p,q) and Hamiltonian H Let (M, \mathcal L) be a mechanical system with the configuration space M and the smooth Lagrangian \mathcal L. Select a standard coordinate system (\boldsymbol,\boldsymbol) on M. The quantities \textstyle p_i(\boldsymbol,\boldsymbol,t) ~\stackrel~ / are called ''momenta''. (Also ''generalized momenta'', ''conjugate momenta'', and ''canonical momenta''). For a time instant t, the Legendre transfor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kubo Formula
The Kubo formula, named for Ryogo Kubo who first presented the formula in 1957, is an equation which expresses the linear response of an observable quantity due to a time-dependent perturbation. Among numerous applications of the Kubo formula, one can calculate the charge and spin susceptibilities of systems of electrons in response to applied electric and magnetic fields. Responses to external mechanical forces and vibrations can be calculated as well. General Kubo formula Consider a quantum system described by the (time independent) Hamiltonian H_0. The expectation value of a physical quantity, described by the operator \hat, can be evaluated as: : \begin \left\langle\hat\right\rangle &= \operatorname\,\left hat\hat\right= \sum_n \left\langle n \left, \hat \ n \right\rangle e^ \\ \hat &= e^ = \sum_n , n \rangle\langle n , e^ \end where Z_0 = \operatorname\,\left hat\rho_0\right/math> is the partition function. Suppose now that just above some time t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ryogo Kubo
was a Japanese mathematical physicist, best known for his works in statistical physics and non-equilibrium statistical mechanics. Work In the early 1950s, Kubo transformed research into the linear response A linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response. Because of its many applications in informatio ... properties of near-equilibrium condensed-matter systems, in particular the understanding of electron transport and conductivity, through the Kubo formalism, a Green's function approach to linear response theory for quantum systems. In 1977 Ryogo Kubo was awarded the Boltzmann Medal ''for his contributions to the theory of non-equilibrium statistical mechanics, and to the theory of fluctuation phenomena''. He is cited particularly for his work in the establishment of the basic relations between transport coefficients and eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Statistics
Particle statistics is a particular description of multiple particles in statistical mechanics. A key prerequisite concept is that of a statistical ensemble (an idealization comprising the state space of possible states of a system, each labeled with a probability) that emphasizes properties of a large system as a whole at the expense of knowledge about parameters of separate particles. When an ensemble describes a system of particles with similar properties, their number is called the particle number and usually denoted by ''N''. Classical statistics In classical mechanics, all particles ( fundamental and composite particles, atoms, molecules, electrons, etc.) in the system are considered distinguishable. This means that individual particles in a system can be tracked. As a consequence, switching the positions of any pair of particles in the system leads to a different configuration of the system. Furthermore, there is no restriction on placing more than one particle in any g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
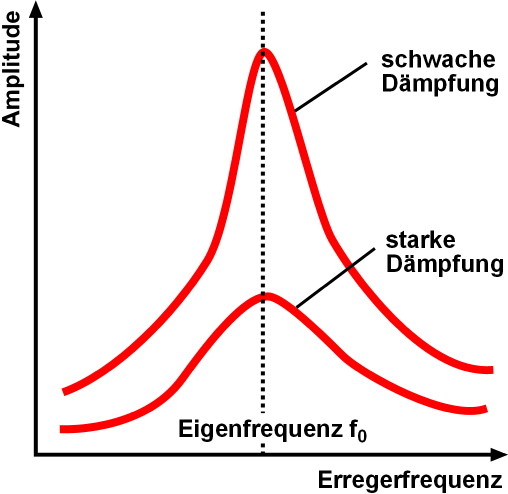
Quality Factor
In physics and engineering, the quality factor or ''Q'' factor is a dimensionless parameter that describes how underdamped an oscillator or resonator is. It is defined as the ratio of the initial energy stored in the resonator to the energy lost in one radian of the cycle of oscillation. Q factor is alternatively defined as the ratio of a resonator's centre frequency to its bandwidth when subject to an oscillating driving force. These two definitions give numerically similar, but not identical, results. Higher ''Q'' indicates a lower rate of energy loss and the oscillations die out more slowly. A pendulum suspended from a high-quality bearing, oscillating in air, has a high ''Q'', while a pendulum immersed in oil has a low one. Resonators with high quality factors have low damping, so that they ring or vibrate longer. Explanation The Q factor is a parameter that describes the resonance behavior of an underdamped harmonic oscillator (resonator). Sinusoidally driven resona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
RLC Circuit
An RLC circuit is an electrical circuit consisting of a resistor (R), an inductor (L), and a capacitor (C), connected in series or in parallel. The name of the circuit is derived from the letters that are used to denote the constituent components of this circuit, where the sequence of the components may vary from RLC. The circuit forms a harmonic oscillator for current, and resonates in a manner similar to an LC circuit. Introducing the resistor increases the decay of these oscillations, which is also known as damping. The resistor also reduces the peak resonant frequency. Some resistance is unavoidable even if a resistor is not specifically included as a component. RLC circuits have many applications as oscillator circuits. Radio receivers and television sets use them for tuning to select a narrow frequency range from ambient radio waves. In this role, the circuit is often referred to as a tuned circuit. An RLC circuit can be used as a band-pass filter, band-stop f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resonance
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillating force is applied at a resonant frequency of a dynamic system, the system will oscillate at a higher amplitude than when the same force is applied at other, non-resonant frequencies. Frequencies at which the response amplitude is a relative maximum are also known as resonant frequencies or resonance frequencies of the system. Small periodic forces that are near a resonant frequency of the system have the ability to produce large amplitude oscillations in the system due to the storage of vibrational energy. Resonance phenomena occur with all types of vibrations or waves: there is mechanical resonance, orbital resonance, acoustic resonance, electromagnetic resonance, nuclear magnetic resonance (NMR), electron spin resonance (E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |