|
Lee Sallows
Lee Cecil Fletcher Sallows (born April 30, 1944) is a British electronics engineer known for his contributions to recreational mathematics. He is particularly noted as the inventor of golygons, self-enumerating sentences, and geomagic squares. Recreational mathematics Sallows is an expert on the theory of magic squares and has invented several variations on them, including alphamagic squares and geomagic squares. The latter invention caught the attention of mathematician Peter Cameron who has said that he believes that "an even deeper structure may lie hidden beyond geomagic squares" In "The lost theorem" published in 1997 he showed that every 3 × 3 magic square is associated with a unique parallelogram on the complex plane, a discovery that had escaped all previous researchers from ancient times down to the present day. In 2014 Sallows discovered a previously unnoticed result involving the medians of a triangle. A golygon is a polygon containing only right ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recreational Mathematics
Recreational mathematics is mathematics carried out for recreation (entertainment) rather than as a strictly research and application-based professional activity or as a part of a student's formal education. Although it is not necessarily limited to being an endeavor for amateurs, many topics in this field require no knowledge of advanced mathematics. Recreational mathematics involves mathematical puzzles and games, often appealing to children and untrained adults, inspiring their further study of the subject. The Mathematical Association of America (MAA) includes recreational mathematics as one of its seventeen Special Interest Groups, commenting: Mathematical competitions (such as those sponsored by mathematical associations) are also categorized under recreational mathematics. Topics Some of the more well-known topics in recreational mathematics are Rubik's Cubes, magic squares, fractals, logic puzzles and mathematical chess problems, but this area of mathematics inc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
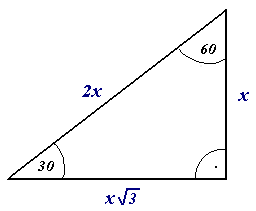
Median (geometry)
In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. Every triangle has exactly three medians, one from each vertex, and they all intersect each other at the triangle's centroid. In the case of isosceles and equilateral triangles, a median bisects any angle at a vertex whose two adjacent sides are equal in length. The concept of a median extends to tetrahedra. Relation to center of mass Each median of a triangle passes through the triangle's centroid, which is the center of mass of an infinitely thin object of uniform density coinciding with the triangle. Thus the object would balance on the intersection point of the medians. The centroid is twice as close along any median to the side that the median intersects as it is to the vertex it emanates from. Equal-area division Each median divides the area of the triangle in half; hence the name, and hence a triangular object of uniform density would ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brocket Hall
Brocket Hall is a neo-classical country house set in a large park at the western side of the urban area of Welwyn Garden City in Hertfordshire, England. The estate is equipped with two golf courses and seven smaller listed buildings, apart from the main house. The freehold on the estate is held by the 3rd Baron Brocket. The house is Grade I-listed. History On the parkland site were two predecessors, the first of which was built in 1239 as Watership or Durantshide Manor, early held variously of Hatfield Manor and the Bishop of Ely. One of these was built about 1430; whereas in 1413 John Mortimer held Waterships it is known in 1477 Thomas Brockett held both manors. The house was acquired by John Brocket in the early 1550s and passed to his son Sir John Brocket (Captain of Queen Elizabeth's personal guard) on his death in 1558. The building and park owe much of their appearance today to Sir Matthew Lamb, 1st Baronet, who purchased the estate in 1746 and commissioned Brocket ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geomagic Square - 4x4 Square Target
Geomagic is the professional engineering software brand of 3D Systems. The brand began when Geomagic Inc., a software company based in Morrisville, North Carolina, was acquired by 3D Systems in February 2013 and combined with that company's other software businesses (namely Rapidform acquired by 3D Systems in October 2012 and Albre in July 2011). Geomagic was founded in 1997 by Ping Fu and Herbert Edelsbrunner. Geomagic-branded software products are focused on computer-aided design, with an emphasis on 3D scanning and other non-traditional design methodologies, such as voxel-based modeling with haptic input. 3D Systems also markets 3D quality inspection software as well as 3D scanners under the Geomagic brand. Geomagic Products 3D Scanning Systems Geomagic Capture is an integrated system consisting of a blue LED structured-light 3D scanner and one of several pieces of application-specific software. The systems are marketed for use as scan-based design tools, wherein a phys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rep-tiles
In the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as a pun on animal reptiles by recreational mathematician Solomon W. Golomb and popularized by Martin Gardner in his "Mathematical Games" column in the May 1963 issue of ''Scientific American''. In 2012 a generalization of rep-tiles called self-tiling tile sets was introduced by Lee Sallows in ''Mathematics Magazine''. Terminology A rep-tile is labelled rep-''n'' if the dissection uses ''n'' copies. Such a shape necessarily forms the prototile for a tiling of the plane, in many cases an aperiodic tiling. A rep-tile dissection using different sizes of the original shape is called an irregular rep-tile or irreptile. If the dissection uses ''n'' copies, the shape is said to be irrep-''n''. If all these sub-tiles are of different sizes then the tiling is additionally described as perfect. A shape that is rep-''n'' or irrep-''n'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-tiling Tile Set
A self-tiling tile set, or ''setiset'', of order ''n'' is a set of ''n'' shapes or pieces, usually planar, each of which can be tiled with smaller replicas of the complete set of ''n'' shapes. That is, the ''n'' shapes can be assembled in ''n'' different ways so as to create larger copies of themselves, where the increase in scale is the same in each case. Figure 1 shows an example for ''n'' = 4 using distinctly shaped decominoes. The concept can be extended to include pieces of higher dimension. The name setisets was coined by Lee Sallows in 2012, but the problem of finding such sets for ''n'' = 4 was asked decades previously by C. Dudley Langford, and examples for polyaboloes (discovered by Martin Gardner, Wade E. Philpott and others) and polyominoes (discovered by Maurice J. Povah) were previously published by Gardner.''Polyhexes and Polyaboloes'' in ''Mathematical Magic Show'', by Martin Gardner, Knopf, 1977, pp 146-159 Examples and definitions From the above definition it fol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Donald Knuth
Donald Ervin Knuth ( ; born January 10, 1938) is an American computer scientist, mathematician, and professor emeritus at Stanford University. He is the 1974 recipient of the ACM Turing Award, informally considered the Nobel Prize of computer science. Knuth has been called the "father of the analysis of algorithms". He is the author of the multi-volume work ''The Art of Computer Programming'' and contributed to the development of the rigorous analysis of the computational complexity of algorithms and systematized formal mathematical techniques for it. In the process, he also popularized the asymptotic notation. In addition to fundamental contributions in several branches of theoretical computer science, Knuth is the creator of the TeX computer typesetting system, the related METAFONT font definition language and rendering system, and the Computer Modern family of typefaces. As a writer and scholar, Knuth created the WEB and CWEB computer programming systems designed to encou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richard K
Richard is a male given name. It originates, via Old French, from Old Frankish and is a compound of the words descending from Proto-Germanic ''*rīk-'' 'ruler, leader, king' and ''*hardu-'' 'strong, brave, hardy', and it therefore means 'strong in rule'. Nicknames include "Richie", "Dick", "Dickon", " Dickie", " Rich", "Rick", " Rico", " Ricky", and more. Richard is a common English, German and French male name. It's also used in many more languages, particularly Germanic, such as Norwegian, Danish, Swedish, Icelandic, and Dutch, as well as other languages including Irish, Scottish, Welsh and Finnish. Richard is cognate with variants of the name in other European languages, such as the Swedish "Rickard", the Catalan "Ricard" and the Italian "Riccardo", among others (see comprehensive variant list below). People named Richard Multiple people with the same name * Richard Andersen (other) * Richard Anderson (other) * Richard Cartwright (other) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martin Gardner
Martin Gardner (October 21, 1914May 22, 2010) was an American popular mathematics and popular science writer with interests also encompassing scientific skepticism, micromagic, philosophy, religion, and literatureespecially the writings of Lewis Carroll, L. Frank Baum, and G. K. Chesterton.Martin (2010) He was also a leading authority on Lewis Carroll. '' The Annotated Alice'', which incorporated the text of Carroll's two Alice books, was his most successful work and sold over a million copies. He had a lifelong interest in magic and illusion and in 1999, MAGIC magazine named him as one of the "100 Most Influential Magicians of the Twentieth Century". He was considered the doyen of American puzzlers. He was a prolific and versatile author, publishing more than 100 books. Gardner was best known for creating and sustaining interest in recreational mathematicsand by extension, mathematics in generalthroughout the latter half of the 20th century, principally through his "Mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Angle
In geometry and trigonometry, a right angle is an angle of exactly 90 degrees or radians corresponding to a quarter turn. If a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. The term is a calque of Latin ''angulus rectus''; here ''rectus'' means "upright", referring to the vertical perpendicular to a horizontal base line. Closely related and important geometrical concepts are perpendicular lines, meaning lines that form right angles at their point of intersection, and orthogonality, which is the property of forming right angles, usually applied to vectors. The presence of a right angle in a triangle is the defining factor for right triangles, making the right angle basic to trigonometry. Etymology The meaning of ''right'' in ''right angle'' possibly refers to the Latin adjective ''rectus'' 'erect, straight, upright, perpendicular'. A Greek equivalent is ''orthos'' 'straight; perpendicular' (see orthogon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed ''polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two together, may be called a polygon. The segments of a polygonal circuit are called its '' edges'' or ''sides''. The points where two edges meet are the polygon's '' vertices'' (singular: vertex) or ''corners''. The interior of a solid polygon is sometimes called its ''body''. An ''n''-gon is a polygon with ''n'' sides; for example, a triangle is a 3-gon. A simple polygon is one which does not intersect itself. Mathematicians are often concerned only with the bounding polygonal chains of simple polygons and they often define a polygon accordingly. A polygonal boundary may be allowed to cross over itself, creating star polygons and other self-intersecting polygons. A polygon is a 2-dimensional example of the more general polytope in any num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |