|
Longitudinal Mode
A longitudinal mode of a resonant cavity is a particular standing wave pattern formed by waves confined in the cavity. The longitudinal modes correspond to the wavelengths of the wave which are reinforced by constructive interference after many reflections from the cavity's reflecting surfaces. All other wavelengths are suppressed by destructive interference. A longitudinal mode pattern has its nodes located axially along the length of the cavity. Transverse modes, with nodes located perpendicular to the axis of the cavity, may also exist. Simple cavity A common example of longitudinal modes are the light wavelengths produced by a laser. In the simplest case, the laser's optical cavity is formed by two opposed plane (flat) mirrors surrounding the gain medium (a plane-parallel or Fabry–Pérot cavity). The allowed modes of the cavity are those where the mirror separation distance ''L'' is equal to an exact multiple of half the wavelength, ''λ'': : L = q \frac where ''q'' i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longitudinal Mode V2
Longitudinal is a geometric term of location which may refer to: * Longitude ** Line of longitude, also called a meridian * Longitudinal engine, an internal combustion engine in which the crankshaft is oriented along the long axis of the vehicle, front to back * Longitudinal mode, a particular standing wave pattern of a resonant cavity formed by waves confined in the cavity * Longitudinal redundancy check, in telecommunication, a form of redundancy check that is applied independently to each of a parallel group of bit streams. * Longitudinal study, a research study that involves repeated observations of the same items over long periods of time — often many decades * Longitudinal voltage, in telecommunication, a voltage induced or appearing along the length of a transmission medium * Longitudinal wave, a wave with oscillations or vibrations along or parallel to their direction of travel * Longitudinal/longitudinally are also anatomical terms of location. See also * Latitudinal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
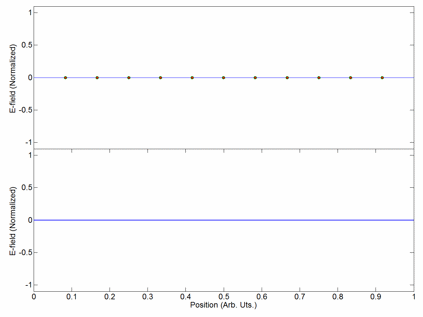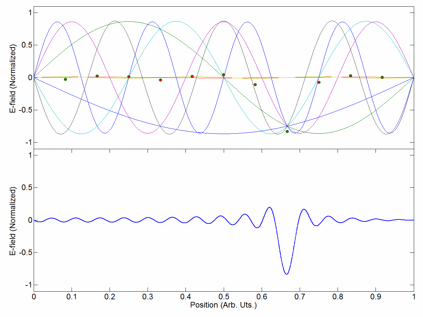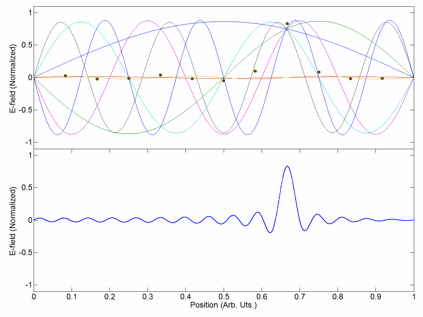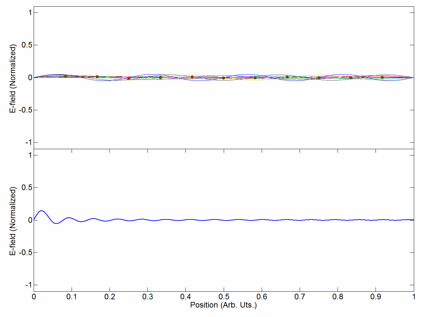
Modelocking
Mode locking is a technique in optics by which a laser can be made to produce pulses of light of extremely short duration, on the order of picoseconds (10−12 s) or femtoseconds (10−15 s). A laser operated in this way is sometimes referred to as a femtosecond laser, for example, in modern refractive surgery. The basis of the technique is to induce a fixed phase relationship between the longitudinal modes of the laser's resonant cavity. Constructive interference between these modes can cause the laser light to be produced as a train of pulses. The laser is then said to be "phase-locked" or "mode-locked". Laser cavity modes Although laser light is perhaps the purest form of light, it is not of a single, pure frequency or wavelength. All lasers produce light over some natural bandwidth or range of frequencies. A laser's bandwidth of operation is determined primarily by the gain medium from which the laser is constructed, and the range of frequencies over which a la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fabry–Pérot Interferometer
In optics, a Fabry–Pérot interferometer (FPI) or etalon is an optical cavity made from two parallel reflecting surfaces (i.e.: thin mirrors). Optical waves can pass through the optical cavity only when they are in resonance with it. It is named after Charles Fabry and Alfred Perot, who developed the instrument in 1899. ''Etalon'' is from the French ''étalon'', meaning "measuring gauge" or "standard". Etalons are widely used in telecommunications, lasers and spectroscopy to control and measure the wavelengths of light. Recent advances in fabrication technique allow the creation of very precise tunable Fabry–Pérot interferometers. The device is technically an interferometer when the distance between the two surfaces (and with it the resonance length) can be changed, and an etalon when the distance is fixed (however, the two terms are often used interchangeably). Basic description The heart of the Fabry–Pérot interferometer is a pair of partially reflective glass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coherent Addition
Coherent addition (or coherent combining) of lasers is a method of power scaling. It allows increasing the output power and brightness of single-transversal mode laser. Usually, the term coherent addition applies to fiber lasers. As the ability of pumping and/or cooling of a single laser is saturated, several similar lasers can be forced to oscillate in phase with a common coupler. The first nonlinear theory of the coherent addition of laser sets had been developed by Nikolay Basov with co-workers in 1965. For Nd:YAG laser set beam combination had been realized by means of SBS phase conjugating mirror. The coherent addition was demonstrated in power scaling of Raman lasers. Limits of coherent addition The addition of lasers reduces the number of longitudinal modes in the output beam; the more lasers are combined, the smaller is the number of longitudinal modes in the output. The simple estimates show that the number of output modes reduces exponentially with the number of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fiber Laser
A fiber laser (or fibre laser in Commonwealth English) is a laser in which the active gain medium is an optical fiber doped with rare-earth elements such as erbium, ytterbium, neodymium, dysprosium, praseodymium, thulium and holmium. They are related to doped fiber amplifiers, which provide light amplification without lasing. Fiber nonlinearities, such as stimulated Raman scattering or four-wave mixing, can also provide gain and thus serve as gain media for a fiber laser. Characteristics An advantage of fiber lasers over other types of lasers is that the laser light is both generated and delivered by an inherently flexible medium, which allows easier delivery to the focusing location and target. This can be important for laser cutting, welding, and folding of metals and polymers. Another advantage is high output power compared to other types of laser. Fiber lasers can have active regions several kilometers long, and so can provide very high optical gain. They can sup ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longitudinal Wave
Longitudinal waves are waves which oscillate in the direction which is parallel to the direction in which the wave travels and displacement of the medium is in the same (or opposite) direction of the wave propagation. Mechanical longitudinal waves are also called ''compressional'' or compression waves, because they produce compression and rarefaction when travelling through a medium, and pressure waves, because they produce increases and decreases in pressure. A wave along the length of a stretched Slinky toy, where the distance between coils increases and decreases, is a good visualization. Real-world examples include sound waves (vibrations in pressure, a particle of displacement, and particle velocity propagated in an elastic medium) and seismic P waves (created by earthquakes and explosions). The other main type of wave is the transverse wave, in which the displacements of the medium are at right angles to the direction of propagation. Transverse waves, for instance, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transverse Wave
In physics, a transverse wave is a wave that oscillates perpendicularly to the direction of the wave's advance. In contrast, a longitudinal wave travels in the direction of its oscillations. All waves move energy from place to place without transporting the matter in the transmission medium if there is one. Electromagnetic waves are transverse without requiring a medium. The designation “transverse” indicates the direction of the wave is perpendicular to the displacement of the particles of the medium through which it passes, or in the case of EM waves, the oscillation is perpendicular to the direction of the wave. A simple example is given by the waves that can be created on a horizontal length of string by anchoring one end and moving the other end up and down. Another example is the waves that are created on the membrane of a drum. The waves propagate in directions that are parallel to the membrane plane, but each point in the membrane itself gets displaced up and dow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Conditions
In the study of differential equations, a boundary-value problem is a differential equation subjected to constraints called boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Boundary value problems arise in several branches of physics as any physical differential equation will have them. Problems involving the wave equation, such as the determination of normal modes, are often stated as boundary value problems. A large class of important boundary value problems are the Sturm–Liouville problems. The analysis of these problems, in the linear case, involves the eigenfunctions of a differential operator. To be useful in applications, a boundary value problem should be well posed. This means that given the input to the problem there exists a unique solution, which depends continuously on the input. Much theoretical work in the field of partial differential equations is devoted t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Equation
The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light waves). It arises in fields like acoustics, electromagnetism, and fluid dynamics. This article focuses on waves in classical physics. Quantum physics uses an operator-based wave equation often as a relativistic wave equation. Introduction The wave equation is a hyperbolic partial differential equation describing waves, including traveling and standing waves; the latter can be considered as linear superpositions of waves traveling in opposite directions. This article mostly focuses on the scalar wave equation describing waves in scalars by scalar functions of a time variable (a variable representing time) and one or more spatial variables (variables representing a position in a space under discussion). At the same time, there a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Path Length
In optics, optical path length (OPL, denoted ''Λ'' in equations), also known as optical length or optical distance, is the length that light needs to travel through a vacuum to create the same phase difference as it would have when traveling through a given medium. It is calculated by taking the product of the geometric length of the optical path followed by light and the refractive index of the homogeneous medium through which the light ray propagates; for inhomogeneous optical media, the product above is generalized as a path integral as part of the ray tracing procedure. A difference in OPL between two paths is often called the optical path difference (OPD). OPL and OPD are important because they determine the phase of the light and govern interference and diffraction of light as it propagates. In a medium of constant refractive index, ''n'', the OPL for a path of geometrical length ''s'' is just :\mathrm = n s .\, If the refractive index varies along the path, the OPL is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Refractive Index
In optics, the refractive index (or refraction index) of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refraction, refracted, when entering a material. This is described by Snell's law of refraction, , where and are the angle of incidence (optics), angle of incidence and angle of refraction, respectively, of a ray crossing the interface between two media with refractive indices and . The refractive indices also determine the amount of light that is reflectivity, reflected when reaching the interface, as well as the critical angle for total internal reflection, their intensity (Fresnel equations) and Brewster's angle. The refractive index, n, can be seen as the factor by which the speed and the wavelength of the radiation are reduced with respect to their vacuum values: the speed of light in a medium is , and similarly the wavelength in that me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |