|
Logics For Computability
Logics for computability are formulations of logic which capture some aspect of computability as a basic notion. This usually involves a mix of special logical connectives as well as semantics which explains how the logic is to be interpreted in a computational way. Probably the first formal treatment of logic for computability is the ''realizability interpretation'' by Stephen Kleene in 1945, who gave an interpretation of intuitionistic number theory in terms of Turing machine computations. His motivation was to make precise the '' Heyting-Brouwer-Kolmogorov (BHK) interpretation'' of intuitionism, according to which proofs of mathematical statements are to be viewed as constructive procedures. With the rise of many other kinds of logic, such as modal logic and linear logic, and novel semantic models, such as game semantics, logics for computability have been formulated in several contexts. Here we mention two. Modal logic for computability Kleene's original realizability interpre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computability
Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science. The computability of a problem is closely linked to the existence of an algorithm to solve the problem. The most widely studied models of computability are the Turing-computable and μ-recursive functions, and the lambda calculus, all of which have computationally equivalent power. Other forms of computability are studied as well: computability notions weaker than Turing machines are studied in automata theory, while computability notions stronger than Turing machines are studied in the field of hypercomputation. Problems A central idea in computability is that of a (computational) problem, which is a task whose computability can be explored. There are two key types of problems: * A decision problem fixes a set ''S'', which may be a set of strings, natural numbers, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martin Hyland
(John) Martin Elliott Hyland is professor of mathematical logic at the University of Cambridge and a fellow of King's College, Cambridge. His interests include mathematical logic, category theory, and theoretical computer science. Education Hyland was educated at the University of Oxford where he was awarded a Doctor of Philosophy degree in 1975 for research supervised by Robin Gandy. Research and career Martin Hyland is best known for his work on category theory applied to logic ( proof theory, recursion theory), theoretical computer science ( lambda-calculus and semantics) and higher-dimensional algebra. In particular he is known for work on the effective topos (within topos theory In mathematics, a topos (, ; plural topoi or , or toposes) is a category that behaves like the category of sheaves of sets on a topological space (or more generally: on a site). Topoi behave much like the category of sets and possess a notion ...) and on game semantics. His former doctoral ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Semantics
Game semantics (german: dialogische Logik, translated as '' dialogical logic'') is an approach to formal semantics that grounds the concepts of truth or validity on game-theoretic concepts, such as the existence of a winning strategy for a player, somewhat resembling Socratic dialogues or medieval theory of Obligationes. History In the late 1950s Paul Lorenzen was the first to introduce a game semantics for logic, and it was further developed by Kuno Lorenz. At almost the same time as Lorenzen, Jaakko Hintikka developed a model-theoretical approach known in the literature as ''GTS'' (game-theoretical semantics). Since then, a number of different game semantics have been studied in logic. Shahid Rahman (Lille) and collaborators developed dialogical logic into a general framework for the study of logical and philosophical issues related to logical pluralism. Beginning 1994 this triggered a kind of renaissance with lasting consequences. This new philosophical impulse experienced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
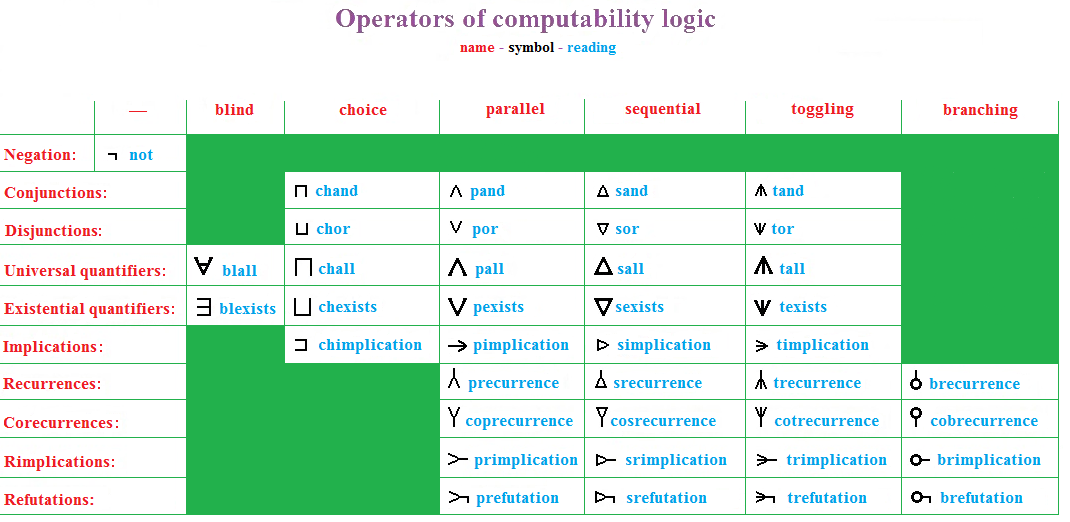
Computability Logic
Computability logic (CoL) is a research program and mathematical framework for redeveloping logic as a systematic formal theory of computability, as opposed to classical logic which is a formal theory of truth. It was introduced and so named by Giorgi Japaridze in 2003. In classical logic, formulas represent true/false statements. In CoL, formulas represent computational problems. In classical logic, the validity of a formula depends only on its form, not on its meaning. In CoL, validity means being always computable. More generally, classical logic tells us when the truth of a given statement always follows from the truth of a given set of other statements. Similarly, CoL tells us when the computability of a given problem ''A'' always follows from the computability of other given problems ''B1,...,Bn''. Moreover, it provides a uniform way to actually construct a solution (algorithm) for such an ''A'' from any known solutions of ''B1,...,Bn''. CoL formulates computational pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Giorgi Japaridze
Giorgi Japaridze (also spelled Giorgie Dzhaparidze) is a Georgian-American researcher in logic and theoretical computer science. He currently holds the title of Full Professor at the Computing Sciences Department of Villanova University. Japaridze is best known for his invention of computability logic, cirquent calculus, and Japaridze's polymodal logic. Research During 1985–1988 Japaridze elaborated the system GLP, known as Japaridze's polymodal logic. This is a system of modal logic with the "necessity" operators …, understood as a natural series of incrementally weak provability predicates for Peano arithmetic. In "The polymodal logic of provability" Japaridze proved the arithmetical completeness of this system, as well as its inherent incompleteness with respect to Kripke frames. GLP has been extensively studied by various authors during the subsequent three decades, especially after Lev Beklemishev, in 2004, pointed out its usefulness in understanding the proof the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dana Scott
Dana Stewart Scott (born October 11, 1932) is an American logician who is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California. His work on automata theory earned him the Turing Award in 1976, while his collaborative work with Christopher Strachey in the 1970s laid the foundations of modern approaches to the semantics of programming languages. He has worked also on modal logic, topology, and category theory. Early career He received his B.A. in Mathematics from the University of California, Berkeley, in 1954. He wrote his Ph.D. thesis on ''Convergent Sequences of Complete Theories'' under the supervision of Alonzo Church while at Princeton, and defended his thesis in 1958. Solomon Feferman (2005) writes of this period: After completing his Ph.D. studies, he moved to the University of Chicago, working as an instructor there until 1960. In 1959, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lars Birkedal
Lars is a common male name in Scandinavian countries. Origin ''Lars'' means "from the city of Laurentum". Lars is derived from the Latin name Laurentius, which means "from Laurentum" or "crowned with laurel". A homonymous Etruscan name was borne by several Etruscan kings, and later used as a last name by the Roman Lartia family. The etymology of the Etruscan name is unknown. People *Lars (bishop), 13th-century Archbishop of Uppsala, Sweden *Lars Kristian Abrahamsen (1855–1921), Norwegian politician *Lars Ahlfors (1907–1996), Finnish Fields Medal recipient *Lars Amble (1939–2015), Swedish actor and director *Lars Herminius Aquilinus, ancient Roman consul *Lars Bak (born 1980), Danish road bicycle racer *Lars Bak (computer programmer) (born 1965), Danish computer programmer *Lars Bender (born 1989), German footballer *Lars Christensen (1884–1965), Norwegian shipowner, whaling magnate and philanthropist *Lars Magnus Ericsson (1846–1926), Swedish inventor * Lars Eriksson, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steve Awodey
Steven M. Awodey (; born 1959) is an American mathematician and logician. He is a Professor of Philosophy and Mathematics at Carnegie Mellon University. Biography Awodey studied mathematics and philosophy at the University of Marburg and the University of Chicago. He earned his Ph.D. from Chicago under Saunders Mac Lane in 1997. He is an active researcher in the areas of category theory and logic, and has also written on the philosophy of mathematics. He is one of the originators of the field of homotopy type theory. He was a member of the School of Mathematics at the Institute for Advanced Study The Institute for Advanced Study (IAS), located in Princeton, New Jersey, in the United States, is an independent center for theoretical research and intellectual inquiry. It has served as the academic home of internationally preeminent scholar ... in 2012–13. Bibliography * * References External links * * * * * {{DEFAULTSORT:Awodey, Steve American logicians 20 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Effective Topos
In mathematics, the effective topos is a topos In mathematics, a topos (, ; plural topoi or , or toposes) is a category that behaves like the category of sheaves of sets on a topological space (or more generally: on a site). Topoi behave much like the category of sets and possess a notio ... introduced by , based on Kleene's notion of recursive realizability, that captures the idea of effectivity in mathematics. References * * * * Topos theory {{cattheory-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intuitionistic Logic
Intuitionistic logic, sometimes more generally called constructive logic, refers to systems of symbolic logic that differ from the systems used for classical logic by more closely mirroring the notion of constructive proof. In particular, systems of intuitionistic logic do not assume the law of the excluded middle and double negation elimination, which are fundamental inference rules in classical logic. Formalized intuitionistic logic was originally developed by Arend Heyting to provide a formal basis for L. E. J. Brouwer's programme of intuitionism. From a proof-theoretic perspective, Heyting’s calculus is a restriction of classical logic in which the law of excluded middle and double negation elimination have been removed. Excluded middle and double negation elimination can still be proved for some propositions on a case by case basis, however, but do not hold universally as they do with classical logic. The standard explanation of intuitionistic logic is the BHK inte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Connective
In logic, a logical connective (also called a logical operator, sentential connective, or sentential operator) is a logical constant. They can be used to connect logical formulas. For instance in the syntax of propositional logic, the binary connective \lor can be used to join the two atomic formulas P and Q, rendering the complex formula P \lor Q . Common connectives include negation, disjunction, conjunction, and implication. In standard systems of classical logic, these connectives are interpreted as truth functions, though they receive a variety of alternative interpretations in nonclassical logics. Their classical interpretations are similar to the meanings of natural language expressions such as English "not", "or", "and", and "if", but not identical. Discrepancies between natural language connectives and those of classical logic have motivated nonclassical approaches to natural language meaning as well as approaches which pair a classical compositional se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Semantics
Game semantics (german: dialogische Logik, translated as '' dialogical logic'') is an approach to formal semantics that grounds the concepts of truth or validity on game-theoretic concepts, such as the existence of a winning strategy for a player, somewhat resembling Socratic dialogues or medieval theory of Obligationes. History In the late 1950s Paul Lorenzen was the first to introduce a game semantics for logic, and it was further developed by Kuno Lorenz. At almost the same time as Lorenzen, Jaakko Hintikka developed a model-theoretical approach known in the literature as ''GTS'' (game-theoretical semantics). Since then, a number of different game semantics have been studied in logic. Shahid Rahman (Lille) and collaborators developed dialogical logic into a general framework for the study of logical and philosophical issues related to logical pluralism. Beginning 1994 this triggered a kind of renaissance with lasting consequences. This new philosophical impulse experienced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |