|
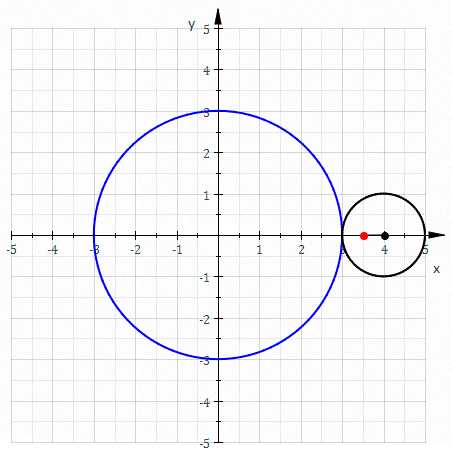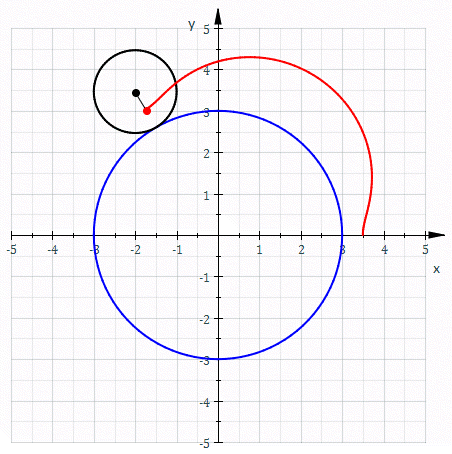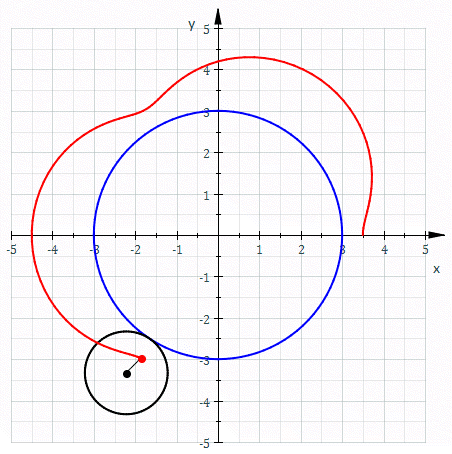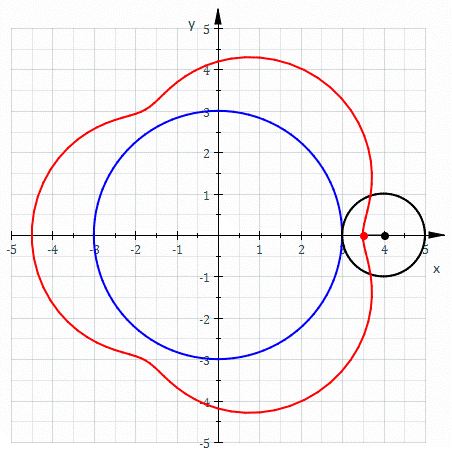
Limaçon
In geometry, a limaçon or limacon , also known as a limaçon of Pascal or Pascal's Snail, is defined as a roulette curve formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller circle is inside the larger circle. Thus, they belong to the family of curves called centered trochoids; more specifically, they are epitrochoids. The cardioid is the special case in which the point generating the roulette lies on the rolling circle; the resulting curve has a cusp. Depending on the position of the point generating the curve, it may have inner and outer loops (giving the family its name), it may be heart-shaped, or it may be oval. A limaçon is a bicircular rational plane algebraic curve of degree 4. History The earliest formal research on limaçons is generally attributed to Étienne Pascal, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limaçon Trisectrix
In geometry, a limaçon trisectrix is the name for the quartic plane curve that is a trisectrix that is specified as a limaçon. The shape of the limaçon trisectrix can be specified by other curves particularly as a rose (mathematics), rose, conchoid (mathematics), conchoid or epitrochoid. The curve is one among a number of plane curve trisectrixes that includes the Conchoid of Nicomedes, the Cycloid of Ceva, Quadratrix of Hippias, Trisectrix of Maclaurin, and Tschirnhausen cubic. The limaçon trisectrix a special case of a sectrix of Maclaurin. Specification and loop structure The limaçon trisectrix specified as a polar equation is :r= a(1+2\cos\theta). The constant a may be positive or negative. The two curves with constants a and -a are reflection symmetry, reflections of each other across the line \theta=\pi/2. The period of r= a(1+2\cos\theta) is 2\pi given the period of the sine wave, sinusoid \cos\theta. The limaçon trisectrix is composed of two loops. * The oute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rose (mathematics)
In mathematics, a rose or rhodonea curve is a sinusoid specified by either the cosine or sine functions with no phase angle that is plotted in polar coordinates. Rose curves or "rhodonea" were named by the Italian mathematician who studied them, Guido Grandi, between the years 1723 and 1728. General overview Specification A rose is the set of points in polar coordinates specified by the polar equation :r=a\cos(k\theta) or in Cartesian coordinates using the parametric equations :x=r\cos(\theta)=a\cos(k\theta)\cos(\theta) :y=r\sin(\theta)=a\cos(k\theta)\sin(\theta). Roses can also be specified using the sine function. Since :\sin(k \theta) = \cos\left( k \theta - \frac \right) = \cos\left( k \left( \theta-\frac \right) \right). Thus, the rose specified by \,r=a\sin(k\theta) is identical to that specified by \,r = a\cos(k\theta) rotated counter-clockwise by \pi/2k radians, which is one-quarter the period of either sinusoid. Since they are specified using the cosine or s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Étienne Pascal
Étienne Pascal (; 2 May 1588 – 24 September 1651) was a French chief tax officer and the father of Blaise Pascal. Biography Pascal was born in Clermont to Martin Pascal, the treasurer of France, and Marguerite Pascal de Mons. He had three daughters, two of whom survived past childhood: Gilberte (1620–?) and Jacqueline (1625–1661). His wife Antoinette Begon died in 1626. He was a tax official, lawyer, and a wealthy member of the '' petite noblesse'', who also had an interest in science and mathematics. He was trained in the law at Paris and received his law degree in 1610. That year, he returned to Clermont and purchased the post of counsellor for Bas-Auvergne, the area surrounding Clermont. In 1631, five years after his wife's death, Pascal moved with his children to Paris. They hired Louise Delfault, a maid who eventually became an instrumental member of the family. Pascal, who never remarried, decided to home-educate his children, who showed extraordinary intellect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardioid
In geometry, a cardioid () is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle. The name was coined by de Castillon in 1741 but the cardioid had been the subject of study decades beforehand.Yates Named for its heart-like form, it is shaped more like the outline of the cross section of a round apple without the stalk. A cardioid microphone exhibits an acoustic pickup pattern that, when graphed in two dimensions, resembles a cardioid (any 2d plane containing the 3d straight line of the microphone body). In three dimensions, the cardioid is shaped like an apple centred around the microphone whi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polar Coordinates
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to the origin of a Cartesian coordinate system) is called the ''pole'', and the ray from the pole in the reference direction is the ''polar axis''. The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth''. Angles in polar notation are generally expressed in either degrees or radians (2 rad being equal to 360°). Grégoire de Saint-Vincent and Bonaventura Cavalieri independently introduced the concepts in the mid-17th century, though the actual term "polar coordinates" has been attributed to Gregorio Fontana in the 18th century. The initial motivation for the introduction of the polar system was the study of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epitrochoid
In geometry, an epitrochoid ( or ) is a roulette traced by a point attached to a circle of radius rolling around the outside of a fixed circle of radius , where the point is at a distance from the center of the exterior circle. The parametric equations for an epitrochoid are :\begin & x (\theta) = (R + r)\cos\theta - d\cos\left(\theta\right) \\ & y (\theta) = (R + r)\sin\theta - d\sin\left(\theta\right) \end The parameter is geometrically the polar angle of the center of the exterior circle. (However, is not the polar angle of the point (x(\theta),y(\theta)) on the epitrochoid.) Special cases include the limaçon with and the epicycloid with . The classic Spirograph toy traces out epitrochoid and hypotrochoid curves. The orbits of planets in the once popular geocentric Ptolemaic system are epitrochoids (see deferent and epicycle). The orbit of the moon, when centered around the sun, approximates an epitrochoid. The combustion chamber of the Wankel engine is an epitro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Algebraic Curve
In geometry, a circular algebraic curve is a type of plane algebraic curve determined by an equation ''F''(''x'', ''y'') = 0, where ''F'' is a polynomial with real coefficients and the highest-order terms of ''F'' form a polynomial divisible by ''x''2 + ''y''2. More precisely, if ''F'' = ''F''''n'' + ''F''''n''−1 + ... + ''F''1 + ''F''0, where each ''F''''i'' is homogeneous of degree ''i'', then the curve ''F''(''x'', ''y'') = 0 is circular if and only if ''F''''n'' is divisible by ''x''2 + ''y''2. Equivalently, if the curve is determined in homogeneous coordinates by ''G''(''x'', ''y'', ''z'') = 0, where ''G'' is a homogeneous polynomial, then the curve is circular if and only if ''G''(1, ''i'', 0) = ''G''(1, −''i'', 0) = 0. In other words, the curve is circular if it contains the circular points at infinity, (1, ''i'', 0) and (1, −''i'',&nbs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference coordinate line is called a ''coordinate axis'' or just ''axis'' (plural ''axes'') of the system, and the point where they meet is its ''origin'', at ordered pair . The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin. One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, ''n'' Cartesian coordinates (an element of real ''n''-space) specify the point in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by the imaginary numbers. The complex plane allows a geometric interpretation of complex numbers. Under addition, they add like vectors. The multiplication of two complex numbers can be expressed more easily in polar coordinates—the magnitude or ''modulus'' of the product is the product of the two absolute values, or moduli, and the angle or ''argument'' of the product is the sum of the two angles, or arguments. In particular, multiplication by a complex number of modulus 1 acts as a rotation. The complex plane is sometimes known as the Argand plane or Gauss plane. Notational conventions Complex numbers In complex analysis, the complex numbers are customarily represented by the symbol ''z'', which can be separated into its real (''x'') a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinusoidal Spiral
In algebraic geometry, the sinusoidal spirals are a family of curves defined by the equation in polar coordinates :r^n = a^n \cos(n \theta)\, where is a nonzero constant and is a rational number other than 0. With a rotation about the origin, this can also be written :r^n = a^n \sin(n \theta).\, The term "spiral" is a misnomer, because they are not actually spirals, and often have a flower-like shape. Many well known curves are sinusoidal spirals including: * Rectangular hyperbola () * Line () * Parabola () * Tschirnhausen cubic () * Cayley's sextet () * Cardioid () * Circle () * Lemniscate of Bernoulli () The curves were first studied by Colin Maclaurin. Equations Differentiating :r^n = a^n \cos(n \theta)\, and eliminating ''a'' produces a differential equation for ''r'' and θ: :\frac\cos n\theta + r\sin n\theta =0. Then :\left(\frac,\ r\frac\right)\cos n\theta \frac = \left(-r\sin n\theta ,\ r \cos n\theta \right) = r\left(-\sin n\theta ,\ \cos n\theta \right) w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Albrecht Dürer
Albrecht Dürer (; ; hu, Ajtósi Adalbert; 21 May 1471 – 6 April 1528),Müller, Peter O. (1993) ''Substantiv-Derivation in Den Schriften Albrecht Dürers'', Walter de Gruyter. . sometimes spelled in English as Durer (without an umlaut) or Duerer, was a German painter, printmaker, and theorist of the German Renaissance The German Renaissance, part of the Northern Renaissance, was a cultural and artistic movement that spread among Germany, German thinkers in the 15th and 16th centuries, which developed from the Italian Renaissance. Many areas of the arts and .... Born in Free Imperial City of Nuremberg, Nuremberg, Dürer established his reputation and influence across Europe in his twenties due to his high-quality List of woodcuts by Dürer, woodcut prints. He was in contact with the major Italian artists of his time, including Raphael, Giovanni Bellini, and Leonardo da Vinci, and from 1512 was patronized by Holy Roman Emperor, Emperor Maximilian I, Holy Roman Emperor, Ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |