|
Leonard Susskind
Leonard Susskind (; born June 16, 1940)his 60th birth anniversary was celebrated with a special symposium at Stanford University.in Geoffrey West's introduction, he gives Suskind's current age as 74 and says his birthday was recent. is an American theoretical physicist, professor of theoretical physics at Stanford University and founding director of the Stanford Institute for Theoretical Physics. His research interests are string theory, quantum field theory, quantum statistical mechanics and quantum cosmology. He is a member of the US National Academy of Sciences, and the American Academy of Arts and Sciences, an associate member of the faculty of Canada's Perimeter Institute for Theoretical Physics, and a distinguished professor of the Korea Institute for Advanced Study. Susskind is widely regarded as one of the fathers of string theory. He was the first to give a precise string-theoretic interpretation of the holographic principle in 1995 and the first to introduce the i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
New York City
New York, often called New York City (NYC), is the most populous city in the United States, located at the southern tip of New York State on one of the world's largest natural harbors. The city comprises five boroughs, each coextensive with a respective county. The city is the geographical and demographic center of both the Northeast megalopolis and the New York metropolitan area, the largest metropolitan area in the United States by both population and urban area. New York is a global center of finance and commerce, culture, technology, entertainment and media, academics, and scientific output, the arts and fashion, and, as home to the headquarters of the United Nations, international diplomacy. With an estimated population in 2024 of 8,478,072 distributed over , the city is the most densely populated major city in the United States. New York City has more than double the population of Los Angeles, the nation's second-most populous city. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black Hole Complementarity
Black hole complementarity is a conjectured solution to the black hole information paradox, proposed by Leonard Susskind, Lárus Thorlacius, John Uglum, and Gerard 't Hooft. Overview Ever since Stephen Hawking suggested information is lost in an evaporating black hole once it passes through the event horizon and is inevitably destroyed at the singularity, and that this can turn pure quantum states into mixed states, some physicists have wondered if a complete theory of quantum gravity might be able to conserve information with a unitary time evolution. But how can this be possible if information cannot escape the event horizon without traveling faster than light? This seems to rule out Hawking radiation as the carrier of the missing information. It also appears as if information cannot be "reflected" at the event horizon as there is nothing special about the horizon locally. Leonard Susskind, Lárus Thorlacius, and John Uglum proposed a radical resolution to this problem by c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fischler–Susskind Mechanism
The Fischler–Susskind mechanism, first proposed by Willy Fischler and Leonard Susskind in 1998, is a holographic prescription based on the particle horizon. The Fischler–Susskind prescription is used to obtain the maximum number of degrees of freedom per Planck volume In particle physics and physical cosmology, Planck units are a system of units of measurement defined exclusively in terms of four universal physical constants: '' c'', '' G'', '' ħ'', and ''k''B (described further below). Expressing one of t ... at the Planck era, compatible with the holographic principle. References Physical cosmology Leonard Susskind {{physical-cosmology-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Staggered Fermion
In lattice field theory, staggered fermions (also known as Kogut–Susskind fermions) are a fermion discretization that reduces the number of fermion doublers from sixteen to four. They are one of the fastest lattice fermions when it comes to simulations and they also possess some nice features such as a remnant chiral symmetry, making them very popular in lattice QCD calculations. Staggered fermions were first formulated by John Kogut and Leonard Susskind in 1975 and were later found to be equivalent to the discretized version of the Dirac–Kähler fermion. Constructing staggered fermions Single-component basis The naively discretized Dirac action in Euclidean spacetime with lattice spacing a and Dirac fields \psi_n at every lattice point, indexed by n = (n_1,n_2,n_3,n_4), takes the form : S = a^4 \sum_\bar \psi_n \bigg(\sum^4_\gamma_\mu \frac+m\psi_n\bigg). Staggered fermions are constructed from this by performing the ''staggered transformation'' into a new basis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Susskind–Glogower Operator
The Susskind–Glogower operator, first proposed by Leonard Susskind and Jonathan Glogower, refers to the operator where the phase is introduced as an approximate polar decomposition of the creation and annihilation operators. It is defined as : V=\fraca, and its adjoint : V^=a^\frac. Their commutation relation is : ,V^, 0\rangle\langle 0, , where , 0\rangle is the vacuum state of the harmonic oscillator. They may be regarded as a (exponential of) phase operator because : Va^a V^=a^a+1, where a^a is the number operator. So the exponential of the phase operator displaces the number operator in the same fashion as the momentum operator In quantum mechanics, the momentum operator is the operator associated with the linear momentum. The momentum operator is, in the position representation, an example of a differential operator. For the case of one particle in one spatial dimensio ... acts as the generator of translations in quantum mechanics: \exp\left(i\frac\right)\h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
RST Model
The Russo–Susskind–Thorlacius model or RST model in short is a modification of the CGHS model to take care of conformal anomalies and render it analytically soluble. In the CGHS model, if we include Faddeev–Popov ghosts to gauge-fix diffeomorphisms in the conformal gauge, they contribute an anomaly of -24. Each matter field contributes an anomaly of 1. So, unless N=24, we will have gravitational anomalies In theoretical physics, a gravitational anomaly is an example of a gauge anomaly: it is an effect of quantum mechanics — usually a one-loop diagram—that invalidates the general covariance of a theory of general relativity combined with some .... To the CGHS action :S_ = \frac \int d^2x\, \sqrt\left\, the following term :S_ = - \frac \int d^2x\, \sqrt \left R\fracR - 2\phi R \right/math> is added, where ''κ'' is either (N-24)/12 or N/12 depending upon whether ghosts are considered. The nonlocal term leads to nonlocality. In the conformal gauge, :S_ = -\frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Worldsheet
In string theory, a worldsheet is a two-dimensional manifold which describes the embedding of a string in spacetime. The term was coined by Leonard Susskind as a direct generalization of the world line concept for a point particle in special and general relativity. The type of string, the geometry of the spacetime in which it propagates, and the presence of long-range background fields (such as gauge fields) are encoded in a two-dimensional conformal field theory defined on the worldsheet. For example, the bosonic string in 26 dimensions has a worldsheet conformal field theory consisting of 26 free scalar bosons. Meanwhile, a superstring worldsheet theory in 10 dimensions consists of 10 free scalar fields and their fermionic superpartners. Mathematical formulation Bosonic string We begin with the classical formulation of the bosonic string. First fix a d-dimensional flat spacetime (d-dimensional Minkowski space), M, which serves as the ambient space for the string. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
String Theory Landscape
In string theory, the string theory landscape (or landscape of vacua) is the collection of possible false vacua,The number of metastable vacua is not known exactly, but commonly quoted estimates are of the order 10500. See M. Douglas, "The statistics of string / M theory vacua", ''JHEP'' 0305, 46 (2003). ; S. Ashok and M. Douglas, "Counting flux vacua", ''JHEP'' 0401, 060 (2004). together comprising a collective "landscape" of choices of parameters governing compactifications. The term "landscape" comes from the notion of a fitness landscape in evolutionary biology. It was first applied to cosmology by Lee Smolin in his book '' The Life of the Cosmos'' (1997), and was first used in the context of string theory by Leonard Susskind. Compactified Calabi–Yau manifolds In string theory the number of flux vacua is commonly thought to be roughly 10^, but could be 10^ or higher. The large number of possibilities arises from choices of Calabi–Yau manifolds and choices of gen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
String Theory
In physics, string theory is a theoretical framework in which the point-like particles of particle physics are replaced by one-dimensional objects called strings. String theory describes how these strings propagate through space and interact with each other. On distance scales larger than the string scale, a string acts like a particle, with its mass, charge, and other properties determined by the vibrational state of the string. In string theory, one of the many vibrational states of the string corresponds to the graviton, a quantum mechanical particle that carries the gravitational force. Thus, string theory is a theory of quantum gravity. String theory is a broad and varied subject that attempts to address a number of deep questions of fundamental physics. String theory has contributed a number of advances to mathematical physics, which have been applied to a variety of problems in black hole physics, early universe cosmology, nuclear physics, and condensed matter ph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Theory (physics)
In theoretical physics, the matrix theory is a quantum mechanical model proposed in 1997 by Tom Banks, Willy Fischler, Stephen Shenker, and Leonard Susskind; it is also known as BFSS matrix model, after the authors' initials. Overview This theory describes the behavior of a set of nine large matrices. In their original paper, these authors showed, among other things, that the low energy limit of this matrix model is described by eleven-dimensional supergravity. These calculations led them to propose that the BFSS matrix model is exactly equivalent to M-theory. The BFSS matrix model can therefore be used as a prototype for a correct formulation of M-theory and a tool for investigating the properties of M-theory in a relatively simple setting. The BFSS matrix model is also considered the worldvolume theory of a large number of D0-branes in Type IIA string theory. Noncommutative geometry In geometry, it is often useful to introduce coordinates. For example, in order to study t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
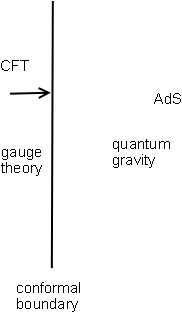
Holographic Principle
The holographic principle is a property of string theories and a supposed property of quantum gravity that states that the description of a volume of space can be thought of as encoded on a lower-dimensional boundary to the region – such as a light-like boundary like a gravitational horizon. First proposed by Gerard 't Hooft, it was given a precise string theoretic interpretation by Leonard Susskind, who combined his ideas with previous ones of 't Hooft and Charles Thorn. Susskind said, "The three-dimensional world of ordinary experience—the universe filled with galaxies, stars, planets, houses, boulders, and people—is a hologram, an image of reality coded on a distant two-dimensional surface." As pointed out by Raphael Bousso, Thorn observed in 1978 that string theory admits a lower-dimensional description in which gravity emerges from it in what would now be called a holographic way. The prime example of holography is the AdS/CFT correspondence. The holographic pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian Lattice Gauge Theory
In physics, Hamiltonian lattice gauge theory is a calculational approach to gauge theory and a special case of lattice gauge theory in which the space is discretized but time is not. The Hamiltonian is then re-expressed as a function of degrees of freedom defined on a d-dimensional lattice. Following Wilson, the spatial components of the vector potential are replaced with Wilson lines over the edges, but the time component is associated with the vertices. However, the temporal gauge is often employed, setting the electric potential to zero. The eigenvalues of the Wilson line operators U(e) (where e is the (oriented) edge in question) take on values on the Lie group G. It is assumed that G is compact, otherwise we run into many problems. The conjugate operator to U(e) is the electric field E(e) whose eigenvalues take on values in the Lie algebra \mathfrak. The Hamiltonian receives contributions coming from the plaquettes (the magnetic contribution) and contributions coming from t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |