|
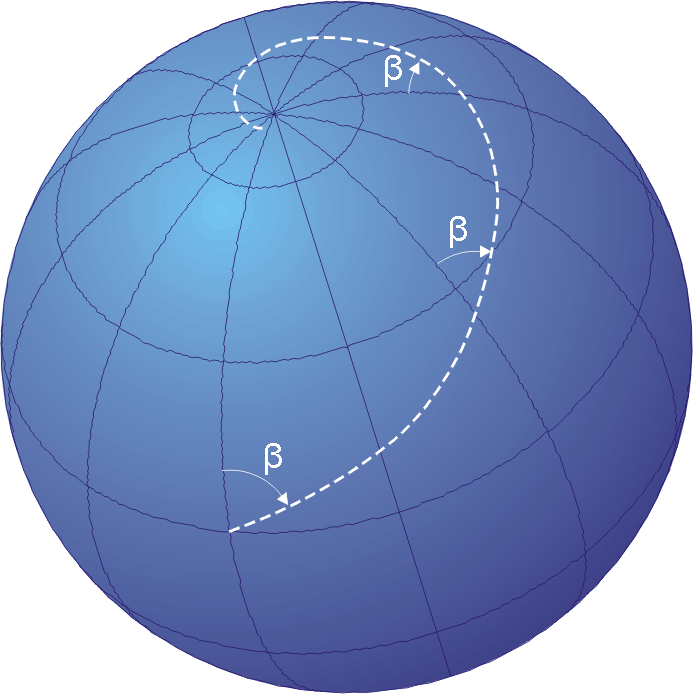
Isoazimuthal
The isoazimuth is the locus of the points on the Earth's surface whose initial orthodromic course with respect to a fixed point is constant. That is, if the initial orthodromic course Z from the starting point ''S'' to the fixed point ''X'' is 80 degrees, the associated isoazimuth is formed by all points whose initial orthodromic course with respect to point ''X'' is 80° (with respect to true north). The isoazimuth is written using the notation ''isoz(X, Z)'' . The isoazimuth is of use when navigating with respect to an object of known location, such as a radio beacon. A straight line called the ''azimuth line of position'' is drawn on a map, and on most common map projections this is a close enough approximation to the isoazimuth. On the Littrow projection, the correspondence is exact. This line is then crossed with an astronomical observation called a Sumner line, and the result gives an estimate of the navigator's position. Isoazimutal on the spherical Earth Let ''X'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great-circle Distance
The great-circle distance, orthodromic distance, or spherical distance is the distance between two points on a sphere, measured along the great-circle arc between them. This arc is the shortest path between the two points on the surface of the sphere. (By comparison, the shortest path passing through the sphere's interior is the chord between the points.) On a curved surface, the concept of straight lines is replaced by a more general concept of geodesics, curves which are locally straight with respect to the surface. Geodesics on the sphere are great circles, circles whose center coincides with the center of the sphere. Any two distinct points on a sphere that are not antipodal (diametrically opposite) both lie on a unique great circle, which the points separate into two arcs; the length of the shorter arc is the great-circle distance between the points. This arc length is proportional to the central angle between the points, which if measured in radians can be scaled u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhumb Line
In navigation, a rhumb line, rhumb (), or loxodrome is an arc crossing all meridians of longitude at the same angle, that is, a path with constant azimuth ( bearing as measured relative to true north). Navigation on a fixed course (i.e., steering the vessel to follow a constant cardinal direction) would result in a rhumb-line track. Introduction The effect of following a rhumb line course on the surface of a globe was first discussed by the Portuguese mathematician Pedro Nunes in 1537, in his ''Treatise in Defense of the Marine Chart'', with further mathematical development by Thomas Harriot in the 1590s. A rhumb line can be contrasted with a great circle, which is the path of shortest distance between two points on the surface of a sphere. On a great circle, the bearing to the destination point does not remain constant. If one were to drive a car along a great circle one would hold the steering wheel fixed, but to follow a rhumb line one would have to turn the wheel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locus (mathematics)
In geometry, a locus (plural: ''loci'') (Latin word for "place", "location") is a set (mathematics), set of all Point (geometry), points (commonly, a line (geometry), line, a line segment, a curve (mathematics), curve or a Surface (topology), surface), whose location satisfies or is determined by one or more specified conditions.. The set of the points that satisfy some property is often called the ''locus of a point'' satisfying this property. The use of the singular in this formulation is a witness that, until the end of the 19th century, mathematicians did not consider infinite sets. Instead of viewing lines and curves as sets of points, they viewed them as places where a point may be ''located'' or may move. History and philosophy Until the beginning of the 20th century, a geometrical shape (for example a curve) was not considered as an infinite set of points; rather, it was considered as an entity on which a point may be located or on which it moves. Thus a circle (mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree (angle)
A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol), is a measurement of a plane (mathematics), plane angle in which one Turn (geometry), full rotation is 360 degrees. It is not an SI unit—the SI unit of angular measure is the radian—but it is mentioned in the SI Brochure, SI brochure as an Non-SI units mentioned in the SI, accepted unit. Because a full rotation equals 2 radians, one degree is equivalent to radians. History The original motivation for choosing the degree as a unit of rotations and angles is unknown. One theory states that it is related to the fact that 360 is approximately the number of days in a year. Ancient astronomers noticed that the sun, which follows through the ecliptic path over the course of the year, seems to advance in its path by approximately one degree each day. Some ancient calendars, such as the Iranian calendar, Persian calendar and the Babylonian calendar, used 360 days for a year. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the motion, movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navigation, marine navigation, air navigation, aeronautic navigation, and space navigation. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks. All navigational techniques involve locating the navigator's Position (geometry), position compared to known locations or patterns. Navigation, in a broader sense, can refer to any skill or study that involves the determination of position and Relative direction, direction. In this sense, navigation includes orienteering and pedestrian navigation. For marine navigation, this involves the safe movement of ships, boats and other nautical craft either on or underneath the water using positions from navigation equipment with appropriate nautical char ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Littrow Projection
The Littrow projection is a map projection developed by Joseph Johann von Littrow in 1833. It is the only conformal, retroazimuthal map projection. As a retroazimuthal projection, the Littrow shows directions, or azimuths, correctly from any point to the center of the map. Patrick Weir of the British Merchant Navy independently reinvented the projection in 1890, after which it began to see more frequent use as recognition of its retroazimuthal property spread. Maps based on the Littrow projection are sometimes referred to as Weir Azimuth diagrams. The projection transforms from latitude ''φ'' and longitude ''λ'' to map coordinates ''x'' and ''y'' via the following equations: :\begin x &= R \frac \\ y &= R \cos \left(\lambda - \lambda_0\right) \tan \varphi \end where ''R'' is the radius of the globe to be projected and ''λ''0 is the longitude desired for the center point. See also * List of map projections This is a summary of map projections that have articles of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sumner Line
Thomas Hubbard Sumner (20 March 1807 – 9 March 1876) was a sea captain during the 19th century. He is best known for developing the celestial navigation method known as the Sumner line or circle of equal altitude. Biography Thomas Hubbard Sumner was born in Boston, Massachusetts, on March 20, 1807, the son of Thomas Waldron Sumner, an architect, and Elizabeth, daughter of Thomas Hubbard, of Weston Massachusetts. Sumner was one of eleven children, four of whom died young. Of the seven that survived he was the only son. He entered Harvard University at age fifteen, graduating in 1826. Shortly after graduating, he married and ran off to New York with a woman with whom he had become entangled but the marriage was short-lived and they were divorced three years later. He then enrolled as a common sailor on a ship engaged in the China trade and within eight years he had risen to the rank of captain and was master of his own ship. On March 10, 1834 he married Selina Christiana Ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Azimuth
An azimuth (; from ) is the horizontal angle from a cardinal direction, most commonly north, in a local or observer-centric spherical coordinate system. Mathematically, the relative position vector from an observer ( origin) to a point of interest is projected perpendicularly onto a reference plane (the horizontal plane); the angle between the projected vector and a reference vector on the reference plane is called the azimuth. When used as a celestial coordinate, the azimuth is the horizontal direction of a star or other astronomical object in the sky. The star is the point of interest, the reference plane is the local area (e.g. a circular area with a 5 km radius at sea level) around an observer on Earth's surface, and the reference vector points to true north. The azimuth is the angle between the north vector and the star's vector on the horizontal plane. Azimuth is usually measured in degrees (°), in the positive range 0° to 360° or in the signed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
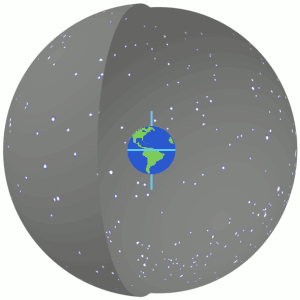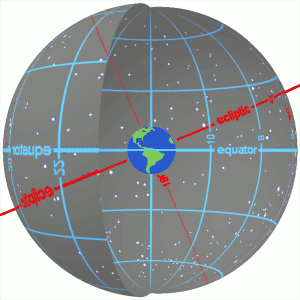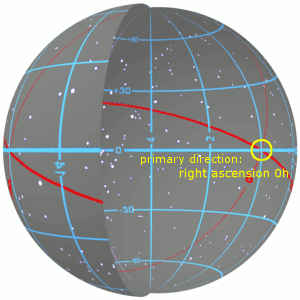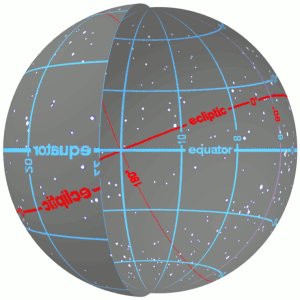
Declination
In astronomy, declination (abbreviated dec; symbol ''δ'') is one of the two angles that locate a point on the celestial sphere in the equatorial coordinate system, the other being hour angle. The declination angle is measured north (positive) or south (negative) of the celestial equator, along the hour circle passing through the point in question. The root of the word ''declination'' (Latin, ''declinatio'') means "a bending away" or "a bending down". It comes from the same root as the words ''incline'' ("bend forward") and ''recline'' ("bend backward"). In some 18th and 19th century astronomical texts, declination is given as ''North Pole Distance'' (N.P.D.), which is equivalent to 90 – (declination). For instance an object marked as declination −5 would have an N.P.D. of 95, and a declination of −90 (the south celestial pole) would have an N.P.D. of 180. Explanation Declination in astronomy is comparable to geographic latitude, projected onto the celestial sphere, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greenwich Hour Angle
In astronomy and celestial navigation, the hour angle is the dihedral angle between the '' meridian plane'' (containing Earth's axis and the zenith) and the ''hour circle'' (containing Earth's axis and a given point of interest). It may be given in degrees, time, or rotations depending on the application. The angle may be expressed as negative east of the meridian plane and positive west of the meridian plane, or as positive westward from 0° to 360°. The angle may be measured in degrees or in time, with 24h = 360° exactly. In celestial navigation, the convention is to measure in degrees westward from the prime meridian (Greenwich hour angle, GHA), from the local meridian (local hour angle, LHA) or from the first point of Aries (sidereal hour angle, SHA). The hour angle is paired with the declination to fully specify the location of a point on the celestial sphere in the equatorial coordinate system. Relation with right ascension The local hour angle (LHA) of an object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point. Discussion Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geometry are the natural analog of straight lines in Euclidean space. For any pair of distinct non- antipodal points on the sphere, there is a unique great circle passing through both. (Every great circle through any point also passes through its antipodal point, so there are infinitely many great circles through two antipodal points.) The shorter of the two great-circle arcs between two distinct points on the sphere is called the ''minor arc'', and is the shortest surface-path between them. Its arc length is the great-circle distance between the points (the intrinsic distance on a sphere), and is proportional to the measure of the central angle formed by the two points and the center of the sphere. A great circle is the largest ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |