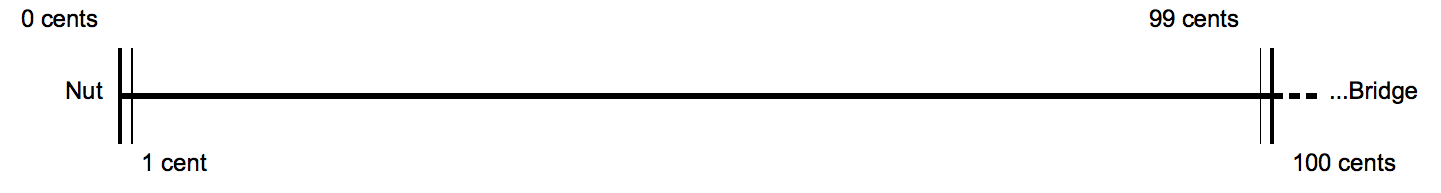|
Interval Ratio
In music, an interval ratio is a ratio of the frequencies of the pitches in a musical interval. For example, a just perfect fifth (for example C to G) is 3:2 (), 1.5, and may be approximated by an equal temperament, equal tempered perfect fifth () which is 27/12 (about 1.498). If the A above middle C is A440 (Concert A), 440 Hertz, Hz, the perfect fifth above it would be E (musical note), E, at (440*1.5=) 660 Hz, while the equal tempered E5 is 659.255 Hz. Ratios, rather than direct frequency measurements, allow musicians to work with relative pitch measurements applicable to many instruments in an intuitive manner, whereas one rarely has the frequencies of fixed pitched instruments memorized and rarely has the capabilities to measure the changes of adjustable pitch instruments (Electronic tuner#Strobe tuner, electronic tuner). Ratios have an Multiplicative inverse, inverse relationship to string length, for example stopping a string at two-thirds (2:3) its length ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Second On C
Major most commonly refers to: * Major (rank), a military rank * Academic major, an academic discipline to which an undergraduate student formally commits * #People, People named Major, including given names, surnames, nicknames * Major and minor in music, an interval, chord, scale, or key * #Sports, Major sport competitions Major(s) or The Major may also refer to: Arts and entertainment Fictional characters * Old Major, a pig in ''Animal Farm'' * Major Major Major Major, in ''Catch-22'' * The Major (Hellsing), The Major (''Hellsing'') * Major (Cinderella), a horse in Disney's ''Cinderella'' * Major Gowen or the Major, in ''Fawlty Towers'' * Motoko Kusanagi or the Major, in ''Ghost in the Shell'' Film, television, theatre and print * ''The Major'', a 1963 BBC natural history documentary film * The Major (film), ''The Major'' (film), a 2013 Russian action film * Major (film), ''Major'' (film), a 2022 Indian biopic * Major (manga), ''Major'' (manga), a sports manga and anime serie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplicative Inverse
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when Multiplication, multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a rational number, fraction ''a''/''b'' is ''b''/''a''. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the Function (mathematics), function ''f''(''x'') that maps ''x'' to 1/''x'', is one of the simplest examples of a function which is its own inverse (an Involution (mathematics), involution). Multiplying by a number is the same as Division (mathematics), dividing by its reciprocal and vice versa. For example, multiplication by 4/5 (or 0.8) will give the same result as division by 5/4 (or 1.25). Therefore, multiplication by a number followed by multiplication by its reciprocal yie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unison
Unison (stylised as UNISON) is a Great Britain, British trade union. Along with Unite the Union, Unite, Unison is one of the two largest trade unions in the United Kingdom, with over 1.2 million members who work predominantly in public services, including local government, education, health and outsourcing, outsourced services. The union was formed in 1993 when three public sector trade unions, the National Association of Local Government Officers, National and Local Government Officers Association (NALGO), the National Union of Public Employees (NUPE) and the Confederation of Health Service Employees (COHSE) merged. UNISON's current general secretary is Christina McAnea, who replaced Dave Prentis in 2021. Members and organisation Members of UNISON are typically from industries within the public sector and generally cover both full-time and part-time support and administrative staff. The majority of people joining UNISON are workers within sectors such as local government, e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Musical Instrument
A musical instrument is a device created or adapted to make Music, musical sounds. In principle, any object that produces sound can be considered a musical instrument—it is through purpose that the object becomes a musical instrument. A person who plays a musical instrument is known as an ''#Instrumentalist, instrumentalist''. The history of musical instruments dates to the beginnings of human culture. Early musical instruments may have been used for rituals, such as a horn (music), horn to signal success on the hunt, or a drum in a religious ceremony. Cultures eventually developed composition and performance of melody, melodies for entertainment. Musical instruments evolved in step with changing applications and technologies. The exact date and specific origin of the first device considered a musical instrument, is widely disputed. The oldest object identified by scholars as a musical instrument, is Divje Babe flute, a simple flute, dated back 50,000–60,000 years. Many scho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Number
An integer is the number zero ( 0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number ( −1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative integers. The set of all integers is often denoted by the boldface or blackboard bold The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the set of natural numbers, the set of integers \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , 5/4, and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meantone Temperament
Meantone temperaments are musical temperaments; that is, a variety of Musical tuning#Tuning systems, tuning systems constructed, similarly to Pythagorean tuning, as a sequence of equal fifths, both rising and descending, scaled to remain within the same octave. But rather than using perfect fifths, consisting of frequency ratios of value 3:2, these are ''tempered'' by a suitable factor that narrows them to ratios that are slightly less than 3:2, in order to bring the major or minor thirds closer to Just intonation, the just intonation ratio of 5:4 or 6:5 , respectively. Among temperaments constructed as a sequence of fifths, a regular temperament is one in which all the fifths are chosen to be of the same size. Twelve-tone equal temperament () is obtained by making all semitones the same size, with each equal to one-twelfth of an octave; i.e. with ratios . Relative to Pythagorean tuning, it narrows the perfect fifths by about 2 cents (music), cents or of a Pythagorean co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Just Intonation
In music, just intonation or pure intonation is a musical tuning, tuning system in which the space between notes' frequency, frequencies (called interval (music), intervals) is a natural number, whole number ratio, ratio. Intervals spaced in this way are said to be pure, and are called just intervals. Just intervals (and chords created by combining them) consist of tones from a single harmonic series (music), harmonic series of an implied fundamental frequency, fundamental. For example, in the diagram, if the notes G3 and C4 (labelled 3 and 4) are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth (music), fourth. In Western musical practice, bowed instruments such as violins, violas, cellos, and double basses are tuned using pure fifths or fourths. In contrast, keyboard instruments are rarely tuned using only pure intervals—the desire fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are determined by choosing a sequence of fifthsBruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: McGraw-Hill). Vol. I: p. 56. which are " pure" or perfect, with ratio 3:2. This is chosen because it is the next harmonic of a vibrating string, after the octave (which is the ratio 2:1), and hence is the next most consonant "pure" interval, and the easiest to tune by ear. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2 (i.e., the untempered perfect fifth), which is ≈ 702 cents wide. The system dates back to Ancient Mesopotamia;. (See .) It is named, and has been widely misattributed, to Ancient Greeks, notably Pythagoras (six ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tuning System
In music, there are two common meanings for tuning: * Tuning practice, the act of tuning an instrument or voice. * Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases. Tuning practice Tuning is the process of adjusting the pitch of one or many tones from musical instruments to establish typical intervals between these tones. Tuning is usually based on a fixed reference, such as A = 440 Hz. The term "''out of tune''" refers to a pitch/tone that is either too high ( sharp) or too low ( flat) in relation to a given reference pitch. While an instrument might be in tune relative to its own range of notes, it may not be considered 'in tune' if it does not match the chosen reference pitch. Some instruments become 'out of tune' with temperature, humidity, damage, or simply time, and must be readjusted or repaired. Different methods of sound production require different methods of adjustment: * Tuning to a pitch with one's vo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each. Typically, cents are used to express small intervals, to check intonation, or to compare the sizes of comparable intervals in different tuning systems. For humans, a single cent is too small to be perceived between successive notes. Cents, as described by Alexander John Ellis, follow a tradition of measuring intervals by logarithms that began with Juan Caramuel y Lobkowitz in the 17th century. Ellis chose to base his measures on the hundredth part of a semitone, \sqrt 200/math>, at Robert Holford Macdowell Bosanquet's suggestion. Making extensive measurements of musical instruments from around the world, Ellis used cents to report and compare the scales employed, and further described and utilized the system in his 1875 edition of Hermann von Helmholtz's ''On the Sensations of Tone''. It has become the standard me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
7-limit
7-limit or septimal tunings and intervals are musical instrument tunings that have a limit of seven: the largest prime factor contained in the interval ratios between pitches is seven. Thus, for example, 50:49 is a 7-limit interval, but 14:11 is not. For example, the greater just minor seventh, 9:5 () is a 5-limit ratio, the harmonic seventh has the ratio 7:4 and is thus a septimal interval. Similarly, the septimal chromatic semitone, 21:20, is a septimal interval as 21÷7=3. The harmonic seventh is used in the barbershop seventh chord and music. () Compositions with septimal tunings include La Monte Young's ''The Well-Tuned Piano'', Ben Johnston's String Quartet No. 4, Lou Harrison's ''Incidental Music for Corneille's Cinna'', and Michael Harrison's ''Revelation: Music in Pure Intonation''. The Great Highland bagpipe is tuned to a ten-note seven-limit scale: 1:1, 9:8, 5:4, 4:3, 27:20, 3:2, 5:3, 7:4, 16:9, 9:5. In the 2nd century Ptolemy described the septima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit (music)
In music theory, limits or harmonic limits are a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term ''limit'' was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name. The harmonic series and the evolution of music Harry Partch, Ivor Darreg, and Ralph David Hill are among the many microtonalists to suggest that music has been slowly evolving to employ higher and higher harmonics in its constructs (see emancipation of the dissonance). In medieval music, only chords made of octaves and perfect fifths (involving relationships among the first three harmonics) were considered consonant. In the West, triadic harmony arose ( contenance angloise) around the time of the Renaissance, and triads quickly became the fundamental building blocks of Western music. The major and minor thirds of these triads invoke relationships among the fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |