|
Hyperbolic
Hyperbolic is an adjective describing something that resembles or pertains to a hyperbola (a curve), to hyperbole (an overstatement or exaggeration), or to hyperbolic geometry. The following phenomena are described as ''hyperbolic'' because they manifest hyperbolas, not because something about them is exaggerated. * Hyperbolic angle, an unbounded variable referring to a hyperbola instead of a circle * Hyperbolic coordinates, location by geometric mean and hyperbolic angle in quadrant I *Hyperbolic distribution, a probability distribution characterized by the logarithm of the probability density function being a hyperbola * Hyperbolic equilibrium point, a fixed point that does not have any center manifolds * Hyperbolic function, an analog of an ordinary trigonometric or circular function * Hyperbolic geometric graph, a random network generated by connecting nearby points sprinkled in a hyperbolic space * Hyperbolic geometry, a non-Euclidean geometry * Hyperbolic group, a finitely ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with: :For any given line ''R'' and point ''P'' not on ''R'', in the plane containing both line ''R'' and point ''P'' there are at least two distinct lines through ''P'' that do not intersect ''R''. (Compare the above with Playfair's axiom, the modern version of Euclid's parallel postulate.) Hyperbolic plane geometry is also the geometry of pseudospherical surfaces, surfaces with a constant negative Gaussian curvature. Saddle surfaces have negative Gaussian curvature in at least some regions, where they locally resemble the hyperbolic plane. A modern use of hyperbolic geometry is in the theory of special relativity, particularly the Minkowski model. When geometers first realised they were working with something other than the standard Euclidean geometry, they described thei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Function
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the unit hyperbola. Also, similarly to how the derivatives of and are and respectively, the derivatives of and are and respectively. Hyperbolic functions occur in the calculations of angles and distances in hyperbolic geometry. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, fluid dynamics, and special relativity. The basic hyperbolic functions are: * hyperbolic sine "" (), * hyperbolic cosine "" (),''Collins Concise Dictionary'', p. 328 from which are derived: * hyperbolic tangent "" () ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Hyperbolas arise in many ways: * as the curve representing the reciprocal function y(x) = 1/x in the Cartesian plane, * as the path followed by the shadow of the tip of a sundial, * as the shape of an open orbit (as distinct from a closed elliptical orbit), such as the orbit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Space
In mathematics, hyperbolic space of dimension n is the unique simply connected, n-dimensional Riemannian manifold of constant sectional curvature equal to -1. It is homogeneous, and satisfies the stronger property of being a symmetric space. There are many ways to construct it as an open subset of \mathbb R^n with an explicitly written Riemannian metric; such constructions are referred to as models. Hyperbolic 2-space, H2, which was the first instance studied, is also called the hyperbolic plane. It is also sometimes referred to as Lobachevsky space or Bolyai–Lobachevsky space after the names of the author who first published on the topic of hyperbolic geometry. Sometimes the qualificative "real" is added to differentiate it from complex hyperbolic spaces, quaternionic hyperbolic spaces and the octononic hyperbolic plane which are the other symmetric spaces of negative curvature. Hyperbolic space serves as the prototype of a Gromov hyperbolic space which is a far-reac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Angle
In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of ''xy'' = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrises the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation. The hyperbola ''xy'' = 1 is rectangular with a semi-major axis of \sqrt 2, analogous to the magnitude of a circular angle corresponding to the area of a circular sector in a circle with radius \sqrt 2. Hyperbolic angle is used as the independent variable for the hyperbolic functions sinh, cosh, and tanh, because these functions may be premised on hyperbolic analogies to the corresponding circular trigonometric functions by regarding a hyperbolic angle as defining a hyperbolic triangle. The parameter thus becomes one of the most useful in the calculus of real variables. Definition Consider the rectangular hyperbo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
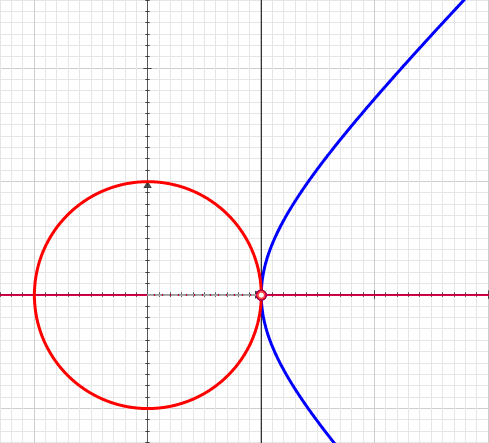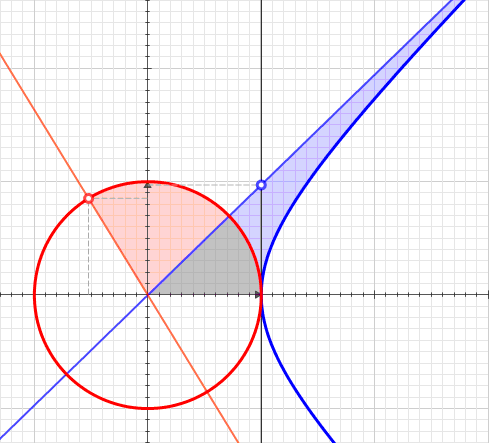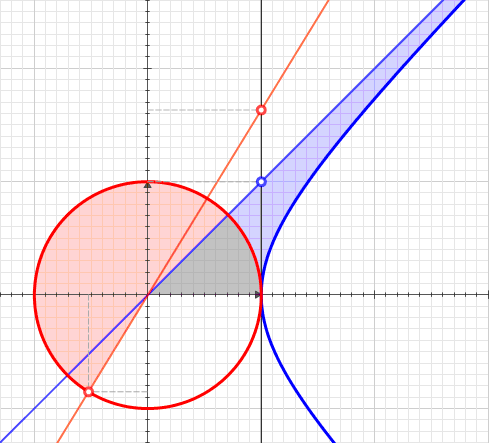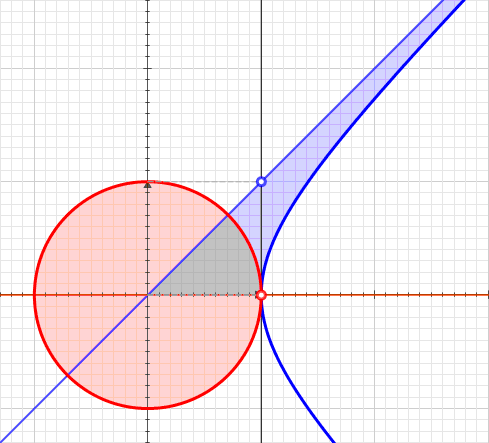
Hyperbolic Sector
A hyperbolic sector is a region of the Cartesian plane bounded by a hyperbola and two rays from the origin to it. For example, the two points and on the rectangular hyperbola , or the corresponding region when this hyperbola is re-scaled and its orientation is altered by a rotation leaving the center at the origin, as with the unit hyperbola. A hyperbolic sector in standard position has and . Hyperbolic sectors are the basis for the hyperbolic functions. Area The area of a hyperbolic sector in standard position is natural logarithm of ''b'' . Proof: Integrate under 1/''x'' from 1 to ''b'', add triangle , and subtract triangle . When in standard position, a hyperbolic sector corresponds to a positive hyperbolic angle at the origin, with the measure of the latter being defined as the area of the former. Hyperbolic triangle When in standard position, a hyperbolic sector determines a hyperbolic triangle, the right triangle with one vertex at the origin, base on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Logarithm
A hyperbolic sector is a region of the Cartesian plane bounded by a hyperbola and two rays from the origin to it. For example, the two points and on the rectangular hyperbola , or the corresponding region when this hyperbola is re-scaled and its orientation is altered by a rotation leaving the center at the origin, as with the unit hyperbola. A hyperbolic sector in standard position has and . Hyperbolic sectors are the basis for the hyperbolic functions. Area The area of a hyperbolic sector in standard position is natural logarithm of ''b'' . Proof: Integrate under 1/''x'' from 1 to ''b'', add triangle , and subtract triangle . When in standard position, a hyperbolic sector corresponds to a positive hyperbolic angle at the origin, with the measure of the latter being defined as the area of the former. Hyperbolic triangle When in standard position, a hyperbolic sector determines a hyperbolic triangle, the right triangle with one vertex at the origin, base on the diag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Soccerball
In geometry, the order-7 truncated triangular tiling, sometimes called the hyperbolic soccerball, is a semiregular tiling of the hyperbolic plane. There are two hexagons and one heptagon on each vertex, forming a pattern similar to a conventional soccer ball (truncated icosahedron) with heptagons in place of pentagons. It has Schläfli symbol of t. Hyperbolic soccerball (football) This tiling is called a hyperbolic soccerball (football) for its similarity to the truncated icosahedron pattern used on soccer balls. Small portions of it as a hyperbolic surface can be constructed in 3-space. Dual tiling The dual tiling is called a ''heptakis heptagonal tiling'', named for being constructible as a heptagonal tiling with every heptagon divided into seven triangles by the center point. : Related tilings This hyperbolic tiling is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (n.6.6), and ,3Coxeter group symmetry. Fro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Group
In group theory, more precisely in geometric group theory, a hyperbolic group, also known as a ''word hyperbolic group'' or ''Gromov hyperbolic group'', is a finitely generated group equipped with a word metric satisfying certain properties abstracted from classical hyperbolic geometry. The notion of a hyperbolic group was introduced and developed by . The inspiration came from various existing mathematical theories: hyperbolic geometry but also low-dimensional topology (in particular the results of Max Dehn concerning the fundamental group of a hyperbolic Riemann surface, and more complex phenomena in three-dimensional topology), and combinatorial group theory. In a very influential (over 1000 citations ) chapter from 1987, Gromov proposed a wide-ranging research program. Ideas and foundational material in the theory of hyperbolic groups also stem from the work of George Mostow, William Thurston, James W. Cannon, Eliyahu Rips, and many others. Definition Let G be a finitely ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Manifold
In mathematics, a hyperbolic manifold is a space where every point looks locally like hyperbolic space of some dimension. They are especially studied in dimensions 2 and 3, where they are called hyperbolic surfaces and hyperbolic 3-manifolds, respectively. In these dimensions, they are important because most manifolds can be made into a hyperbolic manifold by a homeomorphism. This is a consequence of the uniformization theorem for surfaces and the geometrization theorem for 3-manifolds proved by Perelman. Rigorous Definition A hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1. Every complete, connected, simply-connected manifold of constant negative curvature -1 is isometric to the real hyperbolic space \mathbb^n. As a result, the universal cover of any closed manifold M of constant negative curvature -1 is \mathbb^n. Thus, every such M can be written as \mathbb^n/\Gamma where \Gamma is a torsion-free discrete group of isometr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Paraboloid
In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry. Every plane section of a paraboloid by a plane parallel to the axis of symmetry is a parabola. The paraboloid is hyperbolic if every other plane section is either a hyperbola, or two crossing lines (in the case of a section by a tangent plane). The paraboloid is elliptic if every other nonempty plane section is either an ellipse, or a single point (in the case of a section by a tangent plane). A paraboloid is either elliptic or hyperbolic. Equivalently, a paraboloid may be defined as a quadric surface that is not a cylinder, and has an implicit equation whose part of degree two may be factored over the complex numbers into two different linear factors. The paraboloid is hyperbolic if the factors are real; elliptic if the factors are complex conj ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |