|
Homotopy Lifting Property
In mathematics, in particular in homotopy theory within algebraic topology, the homotopy lifting property (also known as an instance of the right lifting property or the covering homotopy axiom) is a technical condition on a continuous function from a topological space ''E'' to another one, ''B''. It is designed to support the picture of ''E'' "above" ''B'' by allowing a homotopy taking place in ''B'' to be moved "upstairs" to ''E''. For example, a covering map has a property of ''unique'' local lifting of paths to a given sheet; the uniqueness is because the fibers of a covering map are discrete spaces. The homotopy lifting property will hold in many situations, such as the projection in a vector bundle, fiber bundle or fibration, where there need be no unique way of lifting. Formal definition Assume all maps are continuous functions between topological spaces. Given a map \pi\colon E \to B, and a space Y\,, one says that (Y, \pi) has the homotopy lifting property, page 7 or t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Lifting Property Bulleted
In topology, two continuous functions from one topological space to another are called homotopic (from and ) if one can be "continuously deformed" into the other, such a deformation being called a homotopy ( ; ) between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology. In practice, there are technical difficulties in using homotopies with certain spaces. Algebraic topologists work with compactly generated spaces, CW complexes, or spectra. Formal definition Formally, a homotopy between two continuous functions ''f'' and ''g'' from a topological space ''X'' to a topological space ''Y'' is defined to be a continuous function H: X \times ,1\to Y from the product of the space ''X'' with the unit interval , 1to ''Y'' such that H(x,0) = f(x) and H(x,1) = g(x) for all x \in X. If we think of the second parameter of ''H'' as time then ''H'' describes a ''continuous def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oxford University Press
Oxford University Press (OUP) is the publishing house of the University of Oxford. It is the largest university press in the world. Its first book was printed in Oxford in 1478, with the Press officially granted the legal right to print books by decree in 1586. It is the second-oldest university press after Cambridge University Press, which was founded in 1534. It is a department of the University of Oxford. It is governed by a group of 15 academics, the Delegates of the Press, appointed by the Vice Chancellor, vice-chancellor of the University of Oxford. The Delegates of the Press are led by the Secretary to the Delegates, who serves as OUP's chief executive and as its major representative on other university bodies. Oxford University Press has had a similar governance structure since the 17th century. The press is located on Walton Street, Oxford, Walton Street, Oxford, opposite Somerville College, Oxford, Somerville College, in the inner suburb of Jericho, Oxford, Jericho. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jeremy Gray
Jeremy John Gray (born 25 April 1947) is an English mathematician primarily interested in the history of mathematics. Biography Gray studied mathematics at the University of Oxford from 1966 to 1969, and then at Warwick University, obtaining his PhD in 1980 under the supervision of Ian Stewart and David Fowler. He has worked at the Open University since 1974, and became a lecturer there in 1978. He also lectured at the University of Warwick from 2002 to 2017, teaching a course on the history of mathematics. Gray was a consultant on the television series, '' The Story of Maths'',''To Infinity and Beyond'' 27 October 2008 21:00 BBC Four a co-production between the Open University and the BBC. He edits Archive for History of Exact Sciences. In 1998 he was an Invited Speaker of the International Congress of Mathematicians in Berlin. In 2012 he became a fellow of the American Mathematical Society. Books Gray has been awarded prizes for his contributions to mathematics, includ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covering Space
In topology, a covering or covering projection is a continuous function, map between topological spaces that, intuitively, Local property, locally acts like a Projection (mathematics), projection of multiple copies of a space onto itself. In particular, coverings are special types of local homeomorphisms. If p : \tilde X \to X is a covering, (\tilde X, p) is said to be a covering space or cover of X, and X is said to be the base of the covering, or simply the base. By abuse of terminology, \tilde X and p may sometimes be called covering spaces as well. Since coverings are local homeomorphisms, a covering space is a special kind of étalé space. Covering spaces first arose in the context of complex analysis (specifically, the technique of analytic continuation), where they were introduced by Bernhard Riemann, Riemann as domains on which naturally multivalued function, multivalued complex functions become single-valued. These spaces are now called Riemann surfaces. Covering spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CW Complex
In mathematics, and specifically in topology, a CW complex (also cellular complex or cell complex) is a topological space that is built by gluing together topological balls (so-called ''cells'') of different dimensions in specific ways. It generalizes both manifolds and simplicial complexes and has particular significance for algebraic topology. It was initially introduced by J. H. C. Whitehead to meet the needs of homotopy theory. (open access) CW complexes have better categorical properties than simplicial complexes, but still retain a combinatorial nature that allows for computation (often with a much smaller complex). The C in CW stands for "closure-finite", and the W for "weak" topology. Definition CW complex A CW complex is constructed by taking the union of a sequence of topological spaces \emptyset = X_ \subset X_0 \subset X_1 \subset \cdots such that each X_k is obtained from X_ by gluing copies of k-cells (e^k_\alpha)_\alpha, each homeomorphic to the open k- bal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibration
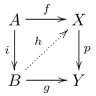
The notion of a fibration generalizes the notion of a fiber bundle and plays an important role in algebraic topology, a branch of mathematics. Fibrations are used, for example, in Postnikov systems or obstruction theory. In this article, all mappings are continuous mappings between topological spaces. Formal definitions Homotopy lifting property A mapping p \colon E \to B satisfies the homotopy lifting property for a space X if: * for every homotopy h \colon X \times , 1\to B and * for every mapping (also called lift) \tilde h_0 \colon X \to E lifting h, _ = h_0 (i.e. h_0 = p \circ \tilde h_0) there exists a (not necessarily unique) homotopy \tilde h \colon X \times , 1\to E lifting h (i.e. h = p \circ \tilde h) with \tilde h_0 = \tilde h, _. The following commutative diagram shows the situation: Fibration A fibration (also called Hurewicz fibration) is a mapping p \colon E \to B satisfying the homotopy lifting property for all spaces X. The space B is called base ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eckmann–Hilton Duality
In the mathematical disciplines of algebraic topology and homotopy theory, Eckmann–Hilton duality in its most basic form, consists of taking a given diagram for a particular concept and reversing the direction of all arrows, much as in category theory with the idea of the opposite category. A significantly deeper form argues that the fact that the dual notion of a limit is a colimit allows us to change the Eilenberg–Steenrod axioms for homology to give axioms for cohomology. It is named after Beno Eckmann and Peter Hilton. Discussion An example is given by currying, which tells us that for any object X, a map X \times I \to Y is the same as a map X \to Y^I, where Y^I is the exponential object, given by all maps from I to Y . In the case of topological spaces, if we take I to be the unit interval, this leads to a duality between X \times I and Y^I, which then gives a duality between the reduced suspension \Sigma X, which is a quotient of X \times I, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Extension Property
In mathematics, in the area of algebraic topology, the homotopy extension property indicates which homotopies defined on a subspace can be extended to a homotopy defined on a larger space. The homotopy extension property of cofibrations is dual to the homotopy lifting property that is used to define fibrations. Definition Let X\,\! be a topological space In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a to ..., and let A \subset X. We say that the pair (X,A)\,\! has the homotopy extension property if, given a homotopy f_\bullet\colon A \rightarrow Y^I and a map \tilde_0\colon X \rightarrow Y such that \tilde_0\circ \iota = \left.\tilde_0\_A = f_0 = \pi_0 \circ f_\bullet, then there exists an ''extension'' of f_\bullet to a homotopy \tilde_\bullet\colon X \rightarrow Y^I such that \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lifting Property
In mathematics, in particular in category theory, the lifting property is a property of a pair of morphisms in a category. It is used in homotopy theory within algebraic topology to define properties of morphisms starting from an explicitly given class of morphisms. It appears in a prominent way in the theory of model categories, an axiomatic framework for homotopy theory introduced by Daniel Quillen. It is also used in the definition of a factorization system, and of a weak factorization system, notions related to but less restrictive than the notion of a model category. Several elementary notions may also be expressed using the lifting property starting from a list of (counter)examples. Formal definition A morphism i in a category has the ''left lifting property'' with respect to a morphism p, and p also has the ''right lifting property'' with respect to i, sometimes denoted i\perp p or i\downarrow p, iff the following implication holds for each morphism f and g in the cat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibration
The notion of a fibration generalizes the notion of a fiber bundle and plays an important role in algebraic topology, a branch of mathematics. Fibrations are used, for example, in Postnikov systems or obstruction theory. In this article, all mappings are continuous mappings between topological spaces. Formal definitions Homotopy lifting property A mapping p \colon E \to B satisfies the homotopy lifting property for a space X if: * for every homotopy h \colon X \times , 1\to B and * for every mapping (also called lift) \tilde h_0 \colon X \to E lifting h, _ = h_0 (i.e. h_0 = p \circ \tilde h_0) there exists a (not necessarily unique) homotopy \tilde h \colon X \times , 1\to E lifting h (i.e. h = p \circ \tilde h) with \tilde h_0 = \tilde h, _. The following commutative diagram shows the situation: Fibration A fibration (also called Hurewicz fibration) is a mapping p \colon E \to B satisfying the homotopy lifting property for all spaces X. The space B is called base ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Theory
In mathematics, homotopy theory is a systematic study of situations in which Map (mathematics), maps can come with homotopy, homotopies between them. It originated as a topic in algebraic topology, but nowadays is learned as an independent discipline. Applications to other fields of mathematics Besides algebraic topology, the theory has also been used in other areas of mathematics such as: * Algebraic geometry (e.g., A1 homotopy theory, A1 homotopy theory) * Category theory (specifically the study of higher category theory, higher categories) Concepts Spaces and maps In homotopy theory and algebraic topology, the word "space" denotes a topological space. In order to avoid Pathological (mathematics), pathologies, one rarely works with arbitrary spaces; instead, one requires spaces to meet extra constraints, such as being Category of compactly generated weak Hausdorff spaces, compactly generated weak Hausdorff or a CW complex. In the same vein as above, a "Map (mathematics), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |