|
Harshad Number
In mathematics, a harshad number (or Niven number) in a given radix, number base is an integer that is divisible by the digit sum, sum of its digits when written in that base. Harshad numbers in base are also known as -harshad (or -Niven) numbers. Because being a Harshad number is determined based on the base the number is expressed in, a number can be a Harshad number many times over. So-called Trans-Harshad numbers are Harshad numbers in every base. Harshad numbers were defined by D. R. Kaprekar, a mathematician from India. The word "harshad" comes from the Sanskrit ' (joy) + ' (give), meaning joy-giver. The term "Niven number" arose from a paper delivered by Ivan M. Niven at a conference on number theory in 1977. Definition Stated mathematically, let be a positive integer with digits when written in base , and let the digits be a_i (i = 0, 1, \ldots, m-1). (It follows that a_i must be either zero or a positive integer up to .) can be expressed as :X=\sum_^ a_i n^i. is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1729 (number)
1729 is the natural number following 1728 and preceding 1730. It is the first nontrivial taxicab number, expressed as the sum of two cubic positive integers in two different ways. It is known as the Ramanujan number or Hardy–Ramanujan number after G. H. Hardy and Srinivasa Ramanujan. As a natural number 1729 is composite, the squarefree product of three prime numbers 7 × 13 × 19. It has as factors 1, 7, 13, 19, 91, 133, 247, and 1729. It is the third Carmichael number, and the first Chernick–Carmichael number. Furthermore, it is the first in the family of absolute Euler pseudoprimes, a subset of Carmichael numbers. 1729 is divisible by 19, the sum of its digits, making it a harshad number in base 10. 1729 is the dimension of the Fourier transform on which the fastest known algorithm for multiplying two numbers is based. This is an example of a galactic algorithm. 1729 can be expressed as the quadratic form. Investigating pairs of its distinct integer-valu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
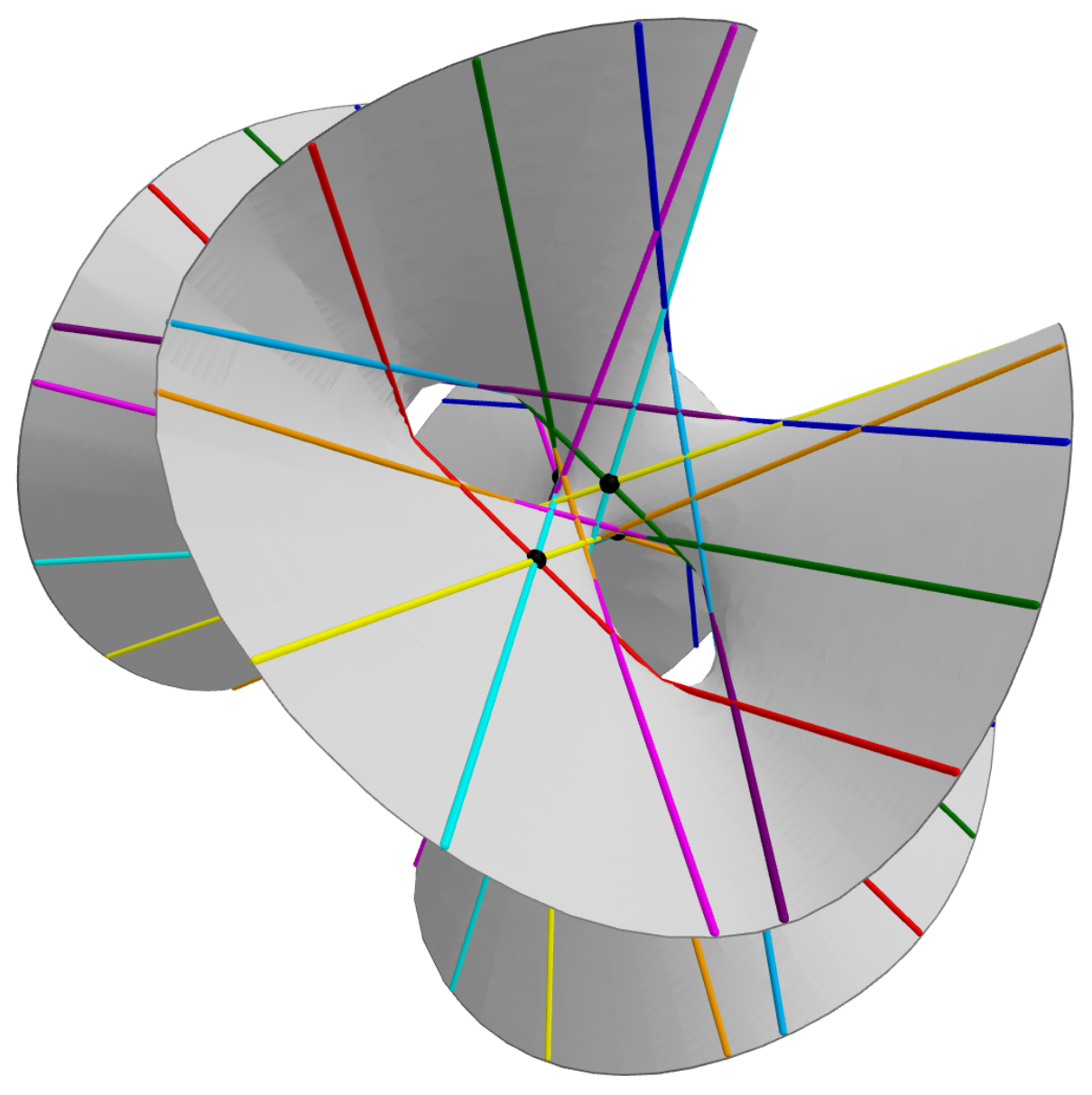
27 (number)
27 (twenty-seven) is the natural number following 26 (number), 26 and preceding 28 (number), 28. Mathematics Including the null-motif, there are 27 distinct Network motif, hypergraph motifs. There are exactly 27 lines on a cubic surface, ''twenty-seven straight lines'' on a smooth cubic surface, which give a basis of the fundamental representation of E6 (mathematics), Lie algebra \mathrm . The unique simple formally real Jordan algebra, the exceptional Jordan algebra of self-adjoint Square matrix, 3 by 3 matrices of quaternions, is 27-dimensional; its automorphism group is the 52-dimensional exceptional Lie algebra \mathrm . There are twenty-seven sporadic groups, if the Tits group, ''non-strict'' group of Lie type \mathrm (with an Faithful representation, irreducible representation that is twice that of \mathrm in 104 dimensions) is included. In Robin's theorem for the Riemann hypothesis, twenty-seven integers fail to hold \sigma(n) < e^\gamma n \log \log n for va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
24 (number)
24 (twenty-four) is the natural number following 23 (number), 23 and preceding 25 (number), 25. It is equal to two dozen and one sixth of a Gross (unit), gross. In mathematics 24 is an Parity (mathematics), even composite number, a highly composite number, an abundant number, a practical number, and a congruent number. The many ways 24 can be constructed inspired a children's mathematical game involving the use of any of the four standard operations on four numbers on a card to get 24 (see 24 (puzzle), 24 Game). 24 is also part of the only nontrivial solution pair to the cannonball problem, and the kissing number in Four-dimensional space, 4-dimensional space. An icositetragon is a regular polygon with 24 sides. A tesseract has 24 two-dimensional square faces. In religion *In Christian apocalyptic literature it represents the complete Church, being the sum of the 12 tribes of Israel and the 12 Apostles in the New Testament, Apostles of the Lamb of God. For example, in ''The Boo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
21 (number)
21 (twenty-one) is the natural number following 20 and preceding 22. The current century is the 21st century AD, under the Gregorian calendar. Mathematics Twenty-one is the fifth distinct semiprime, and the second of the form 3 \times q where q is a higher prime. It is a repdigit in quaternary (1114). Properties As a biprime with proper divisors 1, 3 and 7, twenty-one has a prime aliquot sum of 11 within an aliquot sequence containing only one composite number (21, 11, 1, 0). 21 is the first member of the second cluster of consecutive discrete semiprimes (21, 22), where the next such cluster is ( 33, 34, 35). There are 21 prime numbers with 2 digits. There are a total of 21 prime numbers between 100 and 200. 21 is the first Blum integer, since it is a semiprime with both its prime factors being Gaussian primes. While 21 is the sixth triangular number, it is also the sum of the divisors of the first five positive integers: \begin 1 & + 2 + 3 + 4 + 5 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
20 (number)
20 (twenty) is the natural number following 19 and preceding 21. A group of twenty units is sometimes referred to as a score. In mathematics Twenty is a composite number. It is also the smallest primitive abundant number. The Happy Family of sporadic groups is made up of twenty finite simple groups that are all subquotients of the friendly giant, the largest of twenty-six sporadic groups. Geometry An icosagon is a polygon with 20 edges. Bring's curve is a Riemann surface, whose fundamental polygon is a regular hyperbolic icosagon. Platonic solids The largest number of faces a Platonic solid can have is twenty faces, which make up a regular icosahedron. A dodecahedron, on the other hand, has twenty vertices, likewise the most a regular polyhedron can have. This is because the icosahedron and dodecahdron are duals of each other. Other fields Science 20 is the third magic number in physics. Biology In some countries, the number 20 is used as an index in m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
18 (number)
18 (eighteen) is the natural number following 17 (number), 17 and preceding 19 (number), 19. It is an even composite number. Mathematics 18 is a semiperfect number and an abundant number. It is a largely composite number, as it has 6 divisors and no smaller number has more than 6 divisors. There are 18 One-sided polyomino, one-sided pentominoes. In the classification of finite simple groups, there are 18 infinite families of groups. In science Chemistry * The 18-Electron rule, 18-electron rule is a rule of thumb in transition metal chemistry for characterising and predicting the stability of Metal complex#Metal complexes, metal complexes. In religion and literature * The Hebrew language, Hebrew word for "life" is (''Chai (symbol), chai''), which has a gematria, numerical value of 18. Consequently, the custom has arisen in Jewish circles to give donations and monetary gifts in multiples of 18 as an expression of blessing for long life. * In Judaism, in the Talmud; Pirkei Avot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
10 (number)
10 (ten) is the even natural number following 9 and preceding 11. Ten is the base of the decimal numeral system, the most common system of denoting numbers in both spoken and written language. Name The number "ten" originates from the Proto-Germanic root "*tehun", which in turn comes from the Proto-Indo-European root "*dekm-", meaning "ten". This root is the source of similar words for "ten" in many other Germanic languages, like Dutch, German, and Swedish. The use of "ten" in the decimal system is likely due to the fact that humans have ten fingers and ten toes, which people may have used to count by. Linguistics * A collection of ten items (most often ten years) is called a decade. * The ordinal adjective is ''decimal''; the distributive adjective is ''denary''. * Increasing a quantity by one order of magnitude is most widely understood to mean multiplying the quantity by ten. * To reduce something by one tenth is to '' decimate''. (In ancient Rome, the killing o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
9 (number)
9 (nine) is the natural number following and preceding . Evolution of the Hindu–Arabic digit Circa 300 BC, as part of the Brahmi numerals, various Indians wrote a digit 9 similar in shape to the modern closing question mark without the bottom dot. The Kshatrapa, Andhra and Gupta started curving the bottom vertical line coming up with a -look-alike. How the numbers got to their Gupta form is open to considerable debate. The Nagari continued the bottom stroke to make a circle and enclose the 3-look-alike, in much the same way that the sign @ encircles a lowercase ''a''. As time went on, the enclosing circle became bigger and its line continued beyond the circle downwards, as the 3-look-alike became smaller. Soon, all that was left of the 3-look-alike was a squiggle. The Arabs simply connected that squiggle to the downward stroke at the middle and subsequent European change was purely cosmetic. While the shape of the glyph for the digit 9 has an ascender in most modern typef ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
8 (number)
8 (eight) is the natural number following 7 and preceding 9. Etymology English ''eight'', from Old English '', æhta'', Proto-Germanic ''*ahto'' is a direct continuation of Proto-Indo-European '' *oḱtṓ(w)-'', and as such cognate with Greek and Latin , both of which stems are reflected by the English prefix oct(o)-, as in the ordinal adjective ''octaval'' or ''octavary'', the distributive adjective is '' octonary''. The adjective ''octuple'' (Latin ) may also be used as a noun, meaning "a set of eight items"; the diminutive '' octuplet'' is mostly used to refer to eight siblings delivered in one birth. The Semitic numeral is based on a root ''*θmn-'', whence Akkadian ''smn-'', Arabic ''ṯmn-'', Hebrew ''šmn-'' etc. The Chinese numeral, written ( Mandarin: ''bā''; Cantonese: ''baat''), is from Old Chinese ''*priāt-'', ultimately from Sino-Tibetan ''b-r-gyat'' or ''b-g-ryat'' which also yielded Tibetan '' brgyat''. It has been argued that, as the cardinal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
7 (number)
7 (seven) is the natural number following 6 and preceding 8. It is the only prime number preceding a cube. As an early prime number in the series of positive integers, the number seven has symbolic associations in religion, mythology, superstition and philosophy. The seven classical planets resulted in seven being the number of days in a week. 7 is often considered lucky in Western culture and is often seen as highly symbolic. Evolution of the Arabic digit For early Brahmi numerals, 7 was written more or less in one stroke as a curve that looks like an uppercase vertically inverted (ᒉ). The western Arab peoples' main contribution was to make the longer line diagonal rather than straight, though they showed some tendencies to making the digit more rectilinear. The eastern Arab peoples developed the digit from a form that looked something like 6 to one that looked like an uppercase V. Both modern Arab forms influenced the European form, a two-stroke form consisting of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
5 (number)
5 (five) is a number, numeral and digit. It is the natural number In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive in ..., and cardinal number, following 4 and preceding 6, and is a prime number. Humans, and many other animals, have 5 Digit (anatomy), digits on their Limb (anatomy), limbs. Mathematics 5 is a Fermat prime, a Mersenne prime exponent, as well as a Fibonacci number. 5 is the first congruent number, as well as the length of the hypotenuse of the smallest integer-sided right triangle, making part of the smallest Pythagorean triple (3, 4, 5). 5 is the first safe prime and the first good prime. 11 forms the first pair of sexy primes with 5. 5 is the second Fermat number, Fermat prime, of a total of five known Fermat primes. 5 is also the first of three known Wilso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |