|
Gibbs–Duhem Equation
In thermodynamics, the Gibbs–Duhem equation describes the relationship between changes in chemical potential for components in a thermodynamic system: :\sum_^I N_i \mathrm\mu_i = - S \mathrmT + V \mathrmp where N_i is the number of moles of component i, \mathrm\mu_i the infinitesimal increase in chemical potential for this component, S the entropy, T the absolute temperature, V volume and p the pressure. I is the number of different components in the system. This equation shows that in thermodynamics intensive properties are not independent but related, making it a mathematical statement of the state postulate. When pressure and temperature are variable, only I-1 of I components have independent values for chemical potential and Gibbs' phase rule follows. The Gibbs−Duhem equation cannot be used for small thermodynamic systems due to the influence of surface effects and other microscopic phenomena. The equation is named after Josiah Willard Gibbs and Pierre Duhem. Derivation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamics
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of thermodynamics which convey a quantitative description using measurable macroscopic physical quantities, but may be explained in terms of microscopic constituents by statistical mechanics. Thermodynamics applies to a wide variety of topics in science and engineering, especially physical chemistry, biochemistry, chemical engineering and mechanical engineering, but also in other complex fields such as meteorology. Historically, thermodynamics developed out of a desire to increase the efficiency of early steam engines, particularly through the work of French physicist Sadi Carnot (1824) who believed that engine efficiency was the key that could help France win the Napoleonic Wars. Scots-Irish physicist Lord Kelvin was the firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
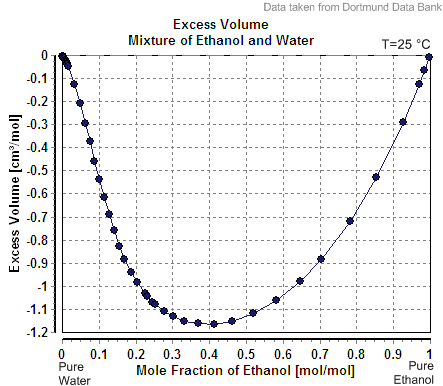
Partial Molar Property
In thermodynamics, a partial molar property is a quantity which describes the variation of an extensive property of a solution or mixture with changes in the molar composition of the mixture at constant temperature and pressure. It is the partial derivative of the extensive property with respect to the amount (number of moles) of the component of interest. Every extensive property of a mixture has a corresponding partial molar property. Definition The partial molar volume is broadly understood as the contribution that a component of a mixture makes to the overall volume of the solution. However, there is more to it than this: When one mole of water is added to a large volume of water at 25 °C, the volume increases by 18 cm3. The molar volume of pure water would thus be reported as 18 cm3 mol−1. However, addition of one mole of water to a large volume of pure ethanol results in an increase in volume of only 14 cm3. The reason that the increase is differ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Darken's Equations
In metallurgy, the Darken equations are used to describe the solid-state diffusion of materials in binary solutions. They were first described by Lawrence Stamper Darken in 1948.Darken, L. S. "Diffusion, mobility and their interrelation through free energy in binary metallic systems". Trans. AIME 175.1 (1948): 184–194. The equations apply to cases where a solid solution's two components do not have the same coefficient of diffusion. The equations Darken's first equation is: : \nu = (D_1 - D_2) \frac = (D_2 - D_1) \frac. where: * \nu is the ''marker velocity'' of inert markers showing the diffusive flux. * D_1 and D_2 are the diffusion coefficients of the two components. * N_1 and N_2 are the atomic fractions of the two components. * x represents the direction in which the diffusion is measured. It is important to note that this equation only holds in situations where the total concentration remains constant. Darken's second equation is: :\tilde = (N_1 D_2 + N_2 D_1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Margules Activity Model
The Margules activity model is a simple thermodynamic model for the excess Gibbs free energy of a liquid mixture introduced in 1895 by Max Margules. After Lewis had introduced the concept of the activity coefficient, the model could be used to derive an expression for the activity coefficients \gamma_i of a compound i in a liquid, a measure for the deviation from ideal solubility, also known as Raoult's law. In chemical engineering the Margules Gibbs free energy model for liquid mixtures is better known as the Margules activity or activity coefficient model. Although the model is old it has the characteristic feature to describe extrema in the activity coefficient, which modern models like NRTL and Wilson cannot. Equations Excess Gibbs free energy Margules expressed the intensive excess Gibbs free energy of a binary liquid mixture as a power series of the mole fractions xi: : \frac=X_1 X_2 (A_ X_1 +A_ X_2) + X_1^2 X_2^2 (B_X_1+ B_ X_2) + ... + X_1^m X_2^m (M_X_1+ M_ X_2) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ternary Plot
A ternary plot, ternary graph, triangle plot, simplex plot, Gibbs triangle or de Finetti diagram is a barycentric plot on three variables which sum to a constant. It graphically depicts the ratios of the three variables as positions in an equilateral triangle. It is used in physical chemistry, petrology, mineralogy, metallurgy, and other physical sciences to show the compositions of systems composed of three species. In population genetics, a triangle plot of genotype frequencies is called a de Finetti diagram. In game theory, it is often called a simplex plot.Karl Tuyls, "An evolutionary game-theoretic analysis of poker strategies", ''Entertainment Computing'' January 2009 , p. 9 Ternary plots are tools for analyzing compositional data in the three-dimensional case. In a ternary plot, the values of the three variables , , and must sum to some constant, . Usually, this constant is represented as 1.0 or 100%. Because for all substances being graphed, any one variab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lawrence Stamper Darken
Lawrence Stamper Darken (18 Sept. 1909, Brooklyn NY – 7 June 1978, State College PA) was a physical chemist and metallurgist, known for his two equations describing solid-state diffusion in binary solutions. He earned his bachelor's degree in mathematics and chemistry from Hamilton College and attained his doctoral degree in physical chemistry at Yale in 1933,Dr. Lawrence S. Darken, 68, Ex.Professor of Mineral Science New York Times, 12 June 1978 followed by two postdoctoral years. From 1935 to 1971 Darken was employed at U.S. Steel Corporation Research Laboratory where he was director of the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vapor Pressure
Vapor pressure (or vapour pressure in English-speaking countries other than the US; see spelling differences) or equilibrium vapor pressure is defined as the pressure exerted by a vapor in thermodynamic equilibrium with its condensed phases (solid or liquid) at a given temperature in a closed system. The equilibrium vapor pressure is an indication of a liquid's evaporation rate. It relates to the tendency of particles to escape from the liquid (or a solid). A substance with a high vapor pressure at normal temperatures is often referred to as '' volatile''. The pressure exhibited by vapor present above a liquid surface is known as vapor pressure. As the temperature of a liquid increases, the kinetic energy of its molecules also increases. As the kinetic energy of the molecules increases, the number of molecules transitioning into a vapor also increases, thereby increasing the vapor pressure. The vapor pressure of any substance increases non-linearly with temperature acco ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
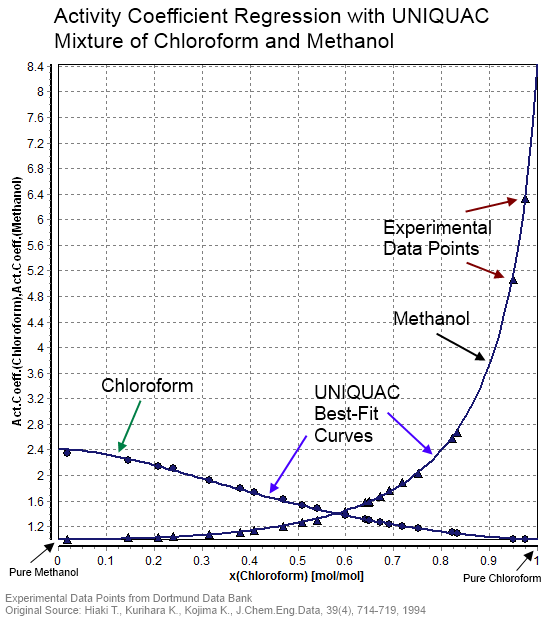
Activity Coefficient
In thermodynamics, an activity coefficient is a factor used to account for deviation of a mixture of chemical substances from ideal behaviour. In an ideal mixture, the microscopic interactions between each pair of chemical species are the same (or macroscopically equivalent, the enthalpy change of solution and volume variation in mixing is zero) and, as a result, properties of the mixtures can be expressed directly in terms of simple concentrations or partial pressures of the substances present e.g. Raoult's law. Deviations from ideality are accommodated by modifying the concentration by an ''activity coefficient''. Analogously, expressions involving gases can be adjusted for non-ideality by scaling partial pressures by a fugacity coefficient. The concept of activity coefficient is closely linked to that of activity in chemistry. Thermodynamic definition The chemical potential, \mu_\mathrm, of a substance B in an ideal mixture of liquids or an ideal solution is given b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isothermal
In thermodynamics, an isothermal process is a type of thermodynamic process in which the temperature ''T'' of a system remains constant: Δ''T'' = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and a change in the system occurs slowly enough to allow the system to be continuously adjusted to the temperature of the reservoir through heat exchange (see quasi-equilibrium). In contrast, an ''adiabatic process'' is where a system exchanges no heat with its surroundings (''Q'' = 0). Simply, we can say that in an isothermal process * T = \text * \Delta T = 0 * dT = 0 * For ideal gases only, internal energy \Delta U = 0 while in adiabatic processes: * Q = 0. Etymology The adjective "isothermal" is derived from the Greek words "ἴσος" ("isos") meaning "equal" and "θέρμη" ("therme") meaning "heat". Examples Isothermal processes can occur in any kind of system that has some means of regulating the temperature, inclu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isobaric Process
In thermodynamics, an isobaric process is a type of thermodynamic process in which the pressure of the system stays constant: Δ''P'' = 0. The heat transferred to the system does work, but also changes the internal energy (''U'') of the system. This article uses the physics sign convention for work, where positive work is work done by the system. Using this convention, by the first law of thermodynamics, : Q = \Delta U + W\, where ''W'' is work, ''U'' is internal energy, and ''Q'' is heat. Pressure-volume work by the closed system is defined as: :W = \int \! p \,dV \, where Δ means change over the whole process, whereas ''d'' denotes a differential. Since pressure is constant, this means that : W = p \Delta V\, . Applying the ideal gas law, this becomes : W = n\,R\,\Delta T with ''R'' representing the gas constant, and ''n'' representing the amount of substance, which is assumed to remain constant (e.g., there is no phase transition during a chemical rea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |