|
Gudermannian Function
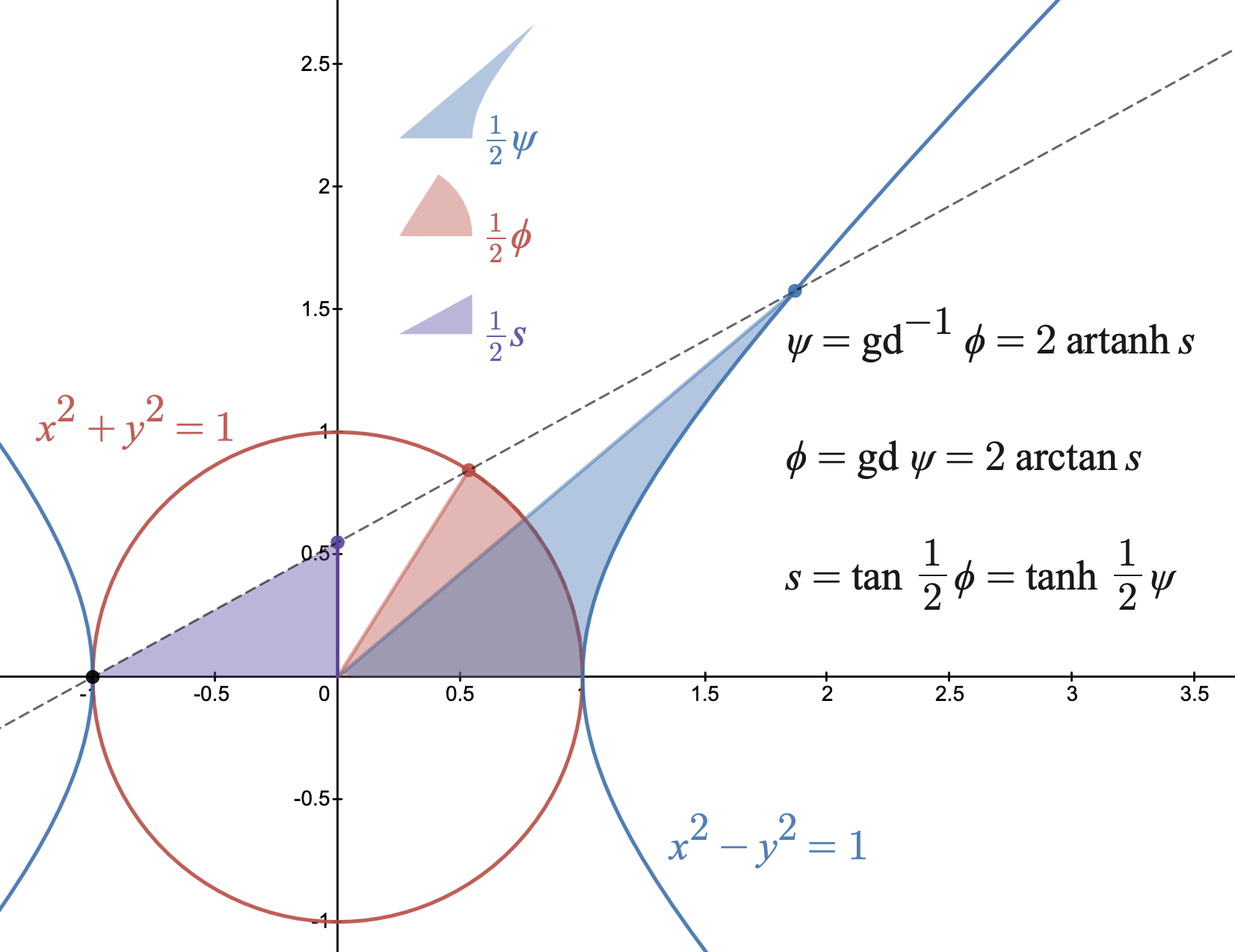
In mathematics, the Gudermannian function relates a hyperbolic angle measure \psi to a circular angle measure \phi called the ''gudermannian'' of \psi and denoted \operatorname\psi. The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude \operatorname(\psi, m) when parameter m=1. The real Gudermannian function is typically defined for -\infty < \psi < \infty to be the integral of the hyperbolic secant : The real inverse Gudermannian function can be defined for |
Integral Of The Secant Function
In calculus, the integral of the secant function can be evaluated using a variety of methods and there are multiple ways of expressing the antiderivative, all of which can be shown to be equivalent via trigonometric identities, :\int \sec \theta \, d\theta = \begin \dfrac12 \ln \dfrac + C \\ 5mu\ln + C \\ 5mu\ln + C \end This formula is useful for evaluating various trigonometric integrals. In particular, it can be used to evaluate the integral of the secant cubed, which, though seemingly special, comes up rather frequently in applications. The definite integral of the secant function starting from 0 is the inverse Gudermannian function, \operatorname^. For numerical applications, all of the above expressions result in loss of significance for some arguments. An alternative expression in terms of the inverse hyperbolic sine is numerically well behaved for real arguments : \operatorname^\phi = \int_0^\phi \sec \theta \, d\theta = \operatorname(\tan \phi). The integral of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, and applied mathematics, as well as in physics, including the branches of hydrodynamics, thermodynamics, quantum mechanics, and twistor theory. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering. As a differentiable function of a complex variable is equal to the sum function given by its Taylor series (that is, it is analytic), complex analysis is particularly concerned with analytic functions of a complex variable, that is, '' holomorphic functions''. The concept can be extended to functions of several complex variables. Complex analysis is contrasted with real analysis, which dea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gudermannian Conformal Map
In mathematics, the Gudermannian function relates a hyperbolic angle measure \psi to a circular angle measure \phi called the ''gudermannian'' of \psi and denoted \operatorname\psi. The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude \operatorname(\psi, m) when parameter m=1. The real Gudermannian function is typically defined for -\infty < \psi < \infty to be the integral of the hyperbolic secant : The real inverse Gudermannian function can be defined for |
Riemann Sphere
In mathematics, the Riemann sphere, named after Bernhard Riemann, is a Mathematical model, model of the extended complex plane (also called the closed complex plane): the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value \infty for infinity. With the Riemann model, the point \infty is near to very large numbers, just as the point 0 is near to very small numbers. The extended complex numbers are useful in complex analysis because they allow for division by zero in some circumstances, in a way that makes expressions such as 1/0=\infty well-behaved. For example, any rational function on the complex plane can be extended to a holomorphic function on the Riemann sphere, with the Pole (complex analysis), poles of the rational function mapping to infinity. More generally, any meromorphic function can be thought of as a holomorphic function whose codomain is the Riemann sphere. In geometr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Möbius Transformation
In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form f(z) = \frac of one complex number, complex variable ; here the coefficients , , , are complex numbers satisfying . Geometrically, a Möbius transformation can be obtained by first applying the inverse stereographic projection from the plane to the unit sphere, moving and rotating the sphere to a new location and orientation in space, and then applying a stereographic projection to map from the sphere back to the plane. These transformations preserve angles, map every straight line to a line or circle, and map every circle to a line or circle. The Möbius transformations are the projective transformations of the complex projective line. They form a group (mathematics), group called the Möbius group, which is the projective linear group . Together with its subgroups, it has numerous applications in mathematics and physics. Möbius geometry, Möbius geometries and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Branch Point
In the mathematical field of complex analysis, a branch point of a multivalued function is a point such that if the function is n-valued (has n values) at that point, all of its neighborhoods contain a point that has more than n values. Multi-valued functions are rigorously studied using Riemann surfaces, and the formal definition of branch points employs this concept. Branch points fall into three broad categories: algebraic branch points, transcendental branch points, and logarithmic branch points. Algebraic branch points most commonly arise from functions in which there is an ambiguity in the extraction of a root, such as solving the equation w^2=z for w as a function of z. Here the branch point is the origin, because the analytic continuation of any solution around a closed loop containing the origin will result in a different function: there is non-trivial monodromy. Despite the algebraic branch point, the function w is well-defined as a multiple-valued function and, in an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gudermannian Identities
In mathematics, the Gudermannian function relates a hyperbolic angle measure \psi to a circular angle measure \phi called the ''gudermannian'' of \psi and denoted \operatorname\psi. The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude \operatorname(\psi, m) when parameter m=1. The real Gudermannian function is typically defined for -\infty < \psi < \infty to be the integral of the hyperbolic secant : The real inverse Gudermannian function can be defined for |
Integration By Substitution
In calculus, integration by substitution, also known as ''u''-substitution, reverse chain rule or change of variables, is a method for evaluating integrals and antiderivatives. It is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule "backwards." This involves differential forms. Substitution for a single variable Introduction (indefinite integrals) Before stating the result rigorously, consider a simple case using indefinite integrals. Compute \int(2x^3+1)^7(x^2)\,dx. Set u=2x^3+1. This means \frac=6x^2, or as a differential form, du=6x^2\,dx. Now: \begin \int(2x^3 +1)^7(x^2)\,dx &= \frac\int\underbrace_\underbrace_ \\ &= \frac\int u^\,du \\ &= \frac\left(\fracu^\right)+C \\ &= \frac(2x^3+1)^+C, \end where C is an arbitrary constant of integration. This procedure is frequently used, but not all integrals are of a form that permits its use. In any event, the result should be verified by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent Half-angle Substitution
In integral calculus, the tangent half-angle substitution is a change of variables used for evaluating integrals, which converts a rational function of trigonometric functions of x into an ordinary rational function of t by setting t = \tan \tfrac x2. This is the one-dimensional stereographic projection of the unit circle parametrized by angle measure onto the real line. The general transformation formula is: \int f(\sin x, \cos x)\, dx =\int f \frac. The tangent of half an angle is important in spherical trigonometry and was sometimes known in the 17th century as the half tangent or semi-tangent. Leonhard Euler used it to evaluate the integral \int dx / (a + b\cos x) in his 1768 integral calculus textbook, and Adrien-Marie Legendre described the general method in 1817. The substitution is described in most integral calculus textbooks since the late 19th century, usually without any special name. It is known in Russia as the universal trigonometric substitution, and also known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, called the imaginary axis, is formed by the imaginary numbers. The complex plane allows for a geometric interpretation of complex numbers. Under addition, they add like vector (geometry), vectors. The multiplication of two complex numbers can be expressed more easily in polar coordinates: the magnitude or ' of the product is the product of the two absolute values, or moduli, and the angle or ' of the product is the sum of the two angles, or arguments. In particular, multiplication by a complex number of modulus 1 acts as a rotation. The complex plane is sometimes called the Argand plane or Gauss plane. Notational conventions Complex numbers In complex analysis, the complex numbers are customarily represented by the symbol , which can be sepa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |