|
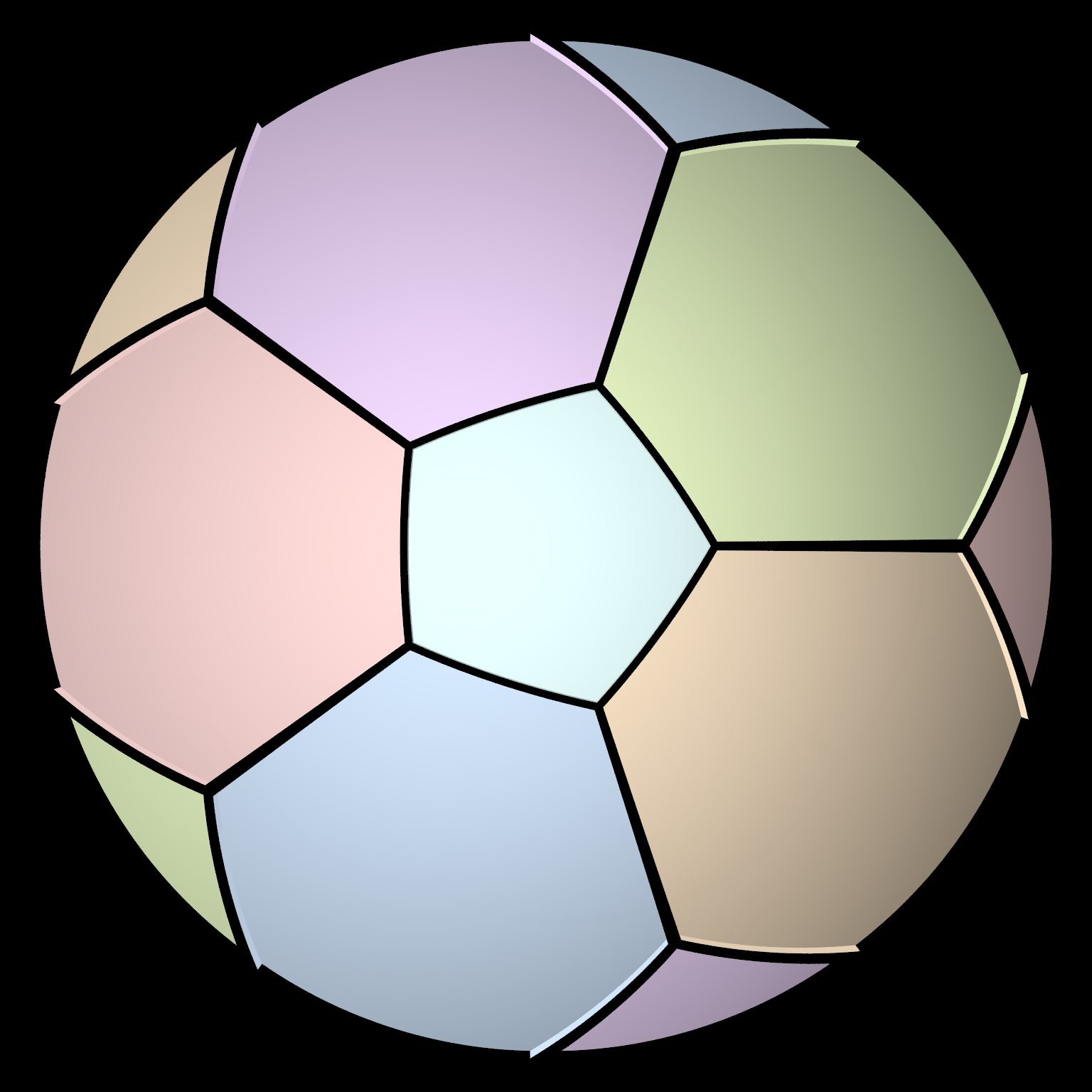
Golomb Graph
In graph theory, the Golomb graph is a polyhedral graph with 10 vertex (graph theory), vertices and 18 edge (graph theory), edges. It is named after Solomon W. Golomb, who constructed it (with a non-planar graph, planar embedding) as a unit distance graph that requires four colors in any graph coloring. Thus, like the simpler Moser spindle, it provides a lower bound for the Hadwiger–Nelson problem: coloring the points of the Euclidean plane so that each unit line segment has differently-colored endpoints requires at least four colors. Construction The method of construction of the Golomb graph as a unit distance graph, by drawing an outer regular polygon connected to an inner twisted polygon or star polygon, has also been used for unit distance representations of the Petersen graph and of generalized Petersen graphs. As with the Moser spindle, the coordinates of the unit-distance embedding of the Golomb graph can be represented in the quadratic field \mathbb[\sqrt]. Fractional ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golomb Lombardi
Golomb or Gollomb is a surname which was changed from the Polisch State Government after 1945 to a phonetical approximation of the polish word "wikt:gołąb, gołąb" (meaning "dove"). It may refer to: *Abraham Golomb (1888–1982) Yiddish-language teacher and writer *Eliyahu Golomb (1893–1945), leader of the Jewish defense effort in Mandate Palestine *Michael Golomb (1909–2008), American mathematician and educator *Rudy Gollomb (1911–1991), American football player *Solomon W. Golomb (1932–2016), American mathematician and engineer ** Golomb ruler ** Golomb coding See also * *Gołąb (surname) Surnames of Jewish origin Polish-language surnames {{Dove-surname ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moser Spindle
In graph theory, a branch of mathematics, the Moser spindle (also called the Mosers' spindle or Moser graph) is an undirected graph, named after mathematicians Leo Moser and his brother William, with seven vertices and eleven edges. It can be drawn as a unit distance graph, and it requires four colors in any graph coloring. Its existence can be used to prove that the Hadwiger–Nelson problem, chromatic number of the plane is at least four.. The Moser spindle has also been called the Hajós graph after György Hajós, as it can be viewed as an instance of the Hajós construction. However, the name "Hajós graph" has also been applied to a different graph, in the form of a triangle inscribed within a hexagon. Construction As a unit distance graph, the Moser spindle is formed by two rhombus, rhombi with 60 and 120 degree angles, so that the sides and short diagonals of the rhombi form equilateral triangles. The two rhombi are placed in the plane, sharing one of their acute-angled ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Chromatic Number
Fractional coloring is a topic in a branch of graph theory known as fractional graph theory. It is a generalization of ordinary graph coloring. In a traditional graph coloring, each vertex in a graph is assigned some color, and adjacent vertices — those connected by edges — must be assigned different colors. In a fractional coloring however, a ''set'' of colors is assigned to each vertex of a graph. The requirement about adjacent vertices still holds, so if two vertices are joined by an edge, they must have no colors in common. Fractional graph coloring can be viewed as the linear programming relaxation of traditional graph coloring. Indeed, fractional coloring problems are much more amenable to a linear programming approach than traditional coloring problems. Definitions A ''b''-fold coloring of a graph ''G'' is an assignment of sets of size ''b'' to vertices of a graph such that adjacent vertices receive disjoint sets. An ''a'':''b''-coloring is a ''b''-fold coloring out ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Field
In algebraic number theory, a quadratic field is an algebraic number field of Degree of a field extension, degree two over \mathbf, the rational numbers. Every such quadratic field is some \mathbf(\sqrt) where d is a (uniquely defined) square-free integer different from 0 and 1. If d>0, the corresponding quadratic field is called a real quadratic field, and, if d<0, it is called an imaginary quadratic field or a complex quadratic field, corresponding to whether or not it is a Field extension, subfield of the field of the real numbers. Quadratic fields have been studied in great depth, initially as part of the theory of binary quadratic forms. There remain some unsolved problems. The class number problem is particularly important. Ring of integers Discriminant For a nonzero square free integer , the Discriminant of an algebraic number field, discriminant of the quadratic field is |
Generalized Petersen Graph
In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized Petersen graph family was introduced in 1950 by H. S. M. Coxeter and was given its name in 1969 by Mark Watkins. Definition and notation In Watkins' notation, ''G''(''n'', ''k'') is a graph with vertex set :\ and edge set :\ where subscripts are to be read modulo ''n'' and ''k'' < ''n''/2. Some authors use the notation ''GPG''(''n'', ''k''). Coxeter's notation for the same graph would be + , a combination of the Schläfli symbols for the regular ''n''-gon and star polygon from which the graph is formed. The Petersen graph itself is ''G''(5, 2) or + . Any generalized Petersen graph can also be constructed from a voltage graph with two vertices, two self-loops, and one other edg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Petersen Graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three- edge-coloring. Although the graph is generally credited to Petersen, it had in fact first appeared 12 years earlier, in a paper by . Kempe observed that its vertices can represent the ten lines of the Desargues configuration, and its edges represent pairs of lines that do not meet at one of the ten points of the configuration. Donald Knuth states that the Petersen graph is "a remarkable configuration that serves as a counterexample to many optimistic predictions about what might be true for graphs in general." The Petersen graph also makes an appearance in tropical geometry. The cone over the Petersen graph is naturally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Segment
In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special case of an ''arc (geometry), arc'', with zero curvature. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using an overline (vinculum (symbol), vinculum) above the symbols for the two endpoints, such as in . Examples of line segments include the sides of a triangle or square. More generally, when both of the segment's end points are vertices of a polygon or polyhedron, the line segment is either an edge (geometry), edge (of that polygon or polyhedron) if they are adjacent vertices, or a diagonal. Wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Plane
In mathematics, a Euclidean plane is a Euclidean space of Two-dimensional space, dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position (geometry), position of each point (mathematics), point. It is an affine space, which includes in particular the concept of parallel lines. It has also measurement, metrical properties induced by a Euclidean distance, distance, which allows to define circles, and angle, angle measurement. A Euclidean plane with a chosen Cartesian coordinate system is called a ''Cartesian plane''. The set \mathbb^2 of the ordered pairs of real numbers (the real coordinate plane), equipped with the dot product, is often called ''the'' Euclidean plane or ''standard Euclidean plane'', since every Euclidean plane is isomorphic to it. History Books I through IV and VI of Euclid's Elements dealt with two-dimensional geometry, developing such notions as similarity of shapes, the Pythagor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hadwiger–Nelson Problem
In geometric graph theory, the Hadwiger–Nelson problem, named after Hugo Hadwiger and Edward Nelson, asks for the minimum number of colors required to color the plane such that no two points at distance 1 from each other have the same color. The answer is unknown, but has been narrowed down to one of the numbers 5, 6 or 7. The correct value may depend on the choice of axioms for set theory. Relation to finite graphs The question can be phrased in graph theoretic terms as follows. Let ''G'' be the unit distance graph of the plane: an infinite graph with all points of the plane as vertices and with an edge between two vertices if and only if the distance between the two points is 1. The Hadwiger–Nelson problem is to find the chromatic number of ''G''. As a consequence, the problem is often called "finding the chromatic number of the plane". By the de Bruijn–Erdős theorem, a result of , the problem is equivalent (under the assumption of the axiom of choice) to that of fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Coloring
In graph theory, graph coloring is a methodic assignment of labels traditionally called "colors" to elements of a Graph (discrete mathematics), graph. The assignment is subject to certain constraints, such as that no two adjacent elements have the same color. Graph coloring is a special case of graph labeling. In its simplest form, it is a way of coloring the Vertex (graph theory), vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an ''edge coloring'' assigns a color to each Edge (graph theory), edges so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each Face (graph theory), face (or region) so that no two faces that share a boundary have the same color. Vertex coloring is often used to introduce graph coloring problems, since other coloring problems can be transformed into a vertex coloring instance. For example, an edge coloring of a graph is just ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solomon W
Solomon (), also called Jedidiah, was the fourth monarch of the Kingdom of Israel and Judah, according to the Hebrew Bible. The successor of his father David, he is described as having been the penultimate ruler of all Twelve Tribes of Israel under an amalgamated Israel and Judah. The hypothesized dates of Solomon's reign are from 970 to 931 BCE. According to the biblical narrative, after Solomon's death, his son and successor Rehoboam adopted harsh policies towards the northern Israelites, who then rejected the reign of the House of David and sought Jeroboam as their king. In the aftermath of Jeroboam's Revolt, the Israelites were split between the Kingdom of Israel in the north (Samaria) and the Kingdom of Judah in the south (Judea); the Bible depicts Rehoboam and the rest of Solomon's patrilineal descendants ruling over independent Judah alone. A Jewish prophet, Solomon is portrayed as wealthy, wise, powerful, and a dedicated follower of Yahweh (God), as attested by t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |