|
Elliptic Space
Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point (rather than two). Because of this, the elliptic geometry described in this article is sometimes referred to as ''single elliptic geometry'' whereas spherical geometry is sometimes referred to as ''double elliptic geometry''. The appearance of this geometry in the nineteenth century stimulated the development of non-Euclidean geometry generally, including hyperbolic geometry. Elliptic geometry has a variety of properties that differ from those of classical Euclidean plane geometry. For example, the sum of the interior angles of any triangle is always greater than 180°. Definitions In elliptic geometry, two lines perpendicular to a given line must intersect. In fact, the perpendiculars o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
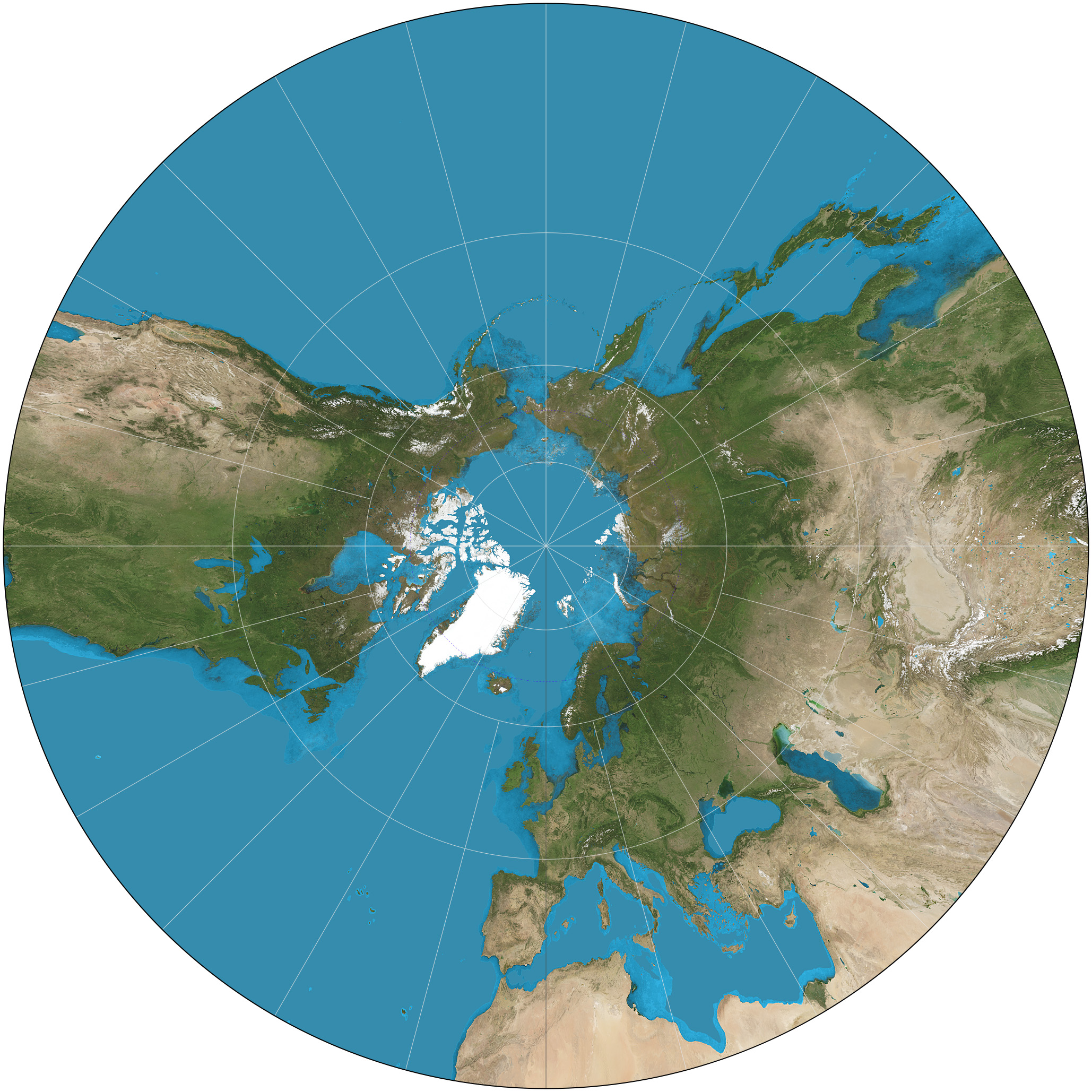
Gnomonic Projection
A gnomonic map projection is a map projection which displays all great circles as straight lines, resulting in any straight line segment on a gnomonic map showing a geodesic, the shortest route between the segment's two endpoints. This is achieved by casting surface points of the sphere onto a tangent plane, each landing where a ray from the center of the sphere passes through the point on the surface and then on to the plane. No distortion occurs at the tangent point, but distortion increases rapidly away from it. Less than half of the sphere can be projected onto a finite map. Consequently, a rectilinear photographic lens, which is based on the gnomonic principle, cannot image more than 180 degrees. History The gnomonic projection is said to be the oldest map projection, developed by Thales for star maps in the 6th century BC. The path of the shadow-tip or light-spot in a nodus-based sundial traces out the same hyperbolae formed by parallels on a gnomonic map. Properties Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
William Rowan Hamilton
Sir William Rowan Hamilton Doctor of Law, LL.D, Doctor of Civil Law, DCL, Royal Irish Academy, MRIA, Royal Astronomical Society#Fellow, FRAS (3/4 August 1805 – 2 September 1865) was an Irish mathematician, astronomer, and physicist. He was the Andrews Professor of Astronomy at Trinity College Dublin, and Royal Astronomer of Ireland, living at Dunsink Observatory. Hamilton's scientific career included the study of geometrical optics, ideas from Fourier analysis, and his work on quaternions which made him one of the founders of modern linear algebra. He made major contributions in optics, classical mechanics and abstract algebra. His work was fundamental to modern theoretical physics, particularly his reformulation of Newtonian mechanics, now called Hamiltonian mechanics. It is now central both to electromagnetism and to quantum mechanics. Early life Hamilton was the fourth of nine children born to Sarah Hutton (1780–1817) and Archibald Hamilton (1778–1819),Bruno (2003) who ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equipollence (geometry)
In Euclidean geometry, equipollence is a binary relation between directed line segments. Two parallel line segments are equipollent when they have the same length and direction. Parallelogram property A definitive feature of Euclidean space is the parallelogram property of vectors: If two segments are equipollent, then they form two sides of a parallelogram: History The concept of equipollent line segments was advanced by Giusto Bellavitis in 1835. Subsequently the term vector was adopted for a class of equipollent line segments. Bellavitis's use of the idea of a relation to compare different but similar objects has become a common mathematical technique, particularly in the use of equivalence relations. Bellavitis used a special notation for the equipollence of segments ''AB'' and ''CD'': :AB \bumpeq CD . The following passages, translated by Michael J. Crowe, show the anticipation that Bellavitis had of vector concepts: :Equipollences continue to hold when one substitute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equivalence Class
In mathematics, when the elements of some set S have a notion of equivalence (formalized as an equivalence relation), then one may naturally split the set S into equivalence classes. These equivalence classes are constructed so that elements a and b belong to the same equivalence class if, and only if, they are equivalent. Formally, given a set S and an equivalence relation \,\sim\, on S, the of an element a in S, denoted by is the set \ of elements which are equivalent to a. It may be proven, from the defining properties of equivalence relations, that the equivalence classes form a partition of S. This partition—the set of equivalence classes—is sometimes called the quotient set or the quotient space of S by \,\sim\,, and is denoted by S / \sim. When the set S has some structure (such as a group operation or a topology) and the equivalence relation \,\sim\, is compatible with this structure, the quotient set often inherits a similar structure from its parent set. Examp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides ''a'', ''b'' and the hypotenuse ''c'', often called the Pythagorean equation: :a^2 + b^2 = c^2 , The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proven numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies the Pythagorean relation: the squared dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemannian Geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a ''Riemannian metric'', i.e. with an inner product on the tangent space at each point that varies smoothly from point to point. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions. Riemannian geometry originated with the vision of Bernhard Riemann expressed in his inaugural lecture "''Ueber die Hypothesen, welche der Geometrie zu Grunde liegen''" ("On the Hypotheses on which Geometry is Based.") It is a very broad and abstract generalization of the differential geometry of surfaces in R3. Development of Riemannian geometry resulted in synthesis of diverse results concerning the geometry of surfaces and the behavior of geodesics on them, with techniques that can be applied to the study of differentiable manifolds of higher dim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-Euclidean Geometry
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises by either replacing the parallel postulate with an alternative, or relaxing the metric requirement. In the former case, one obtains hyperbolic geometry and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras, which give rise to kinematic geometries that have also been called non-Euclidean geometry. The essential difference between the metric geometries is the nature of parallel lines. Euclid's fifth postulate, the parallel postulate, is equivalent to Playfair's postulate, which states that, within a two-dimensional plane, for any given line and a point ''A'', which is not on , there is exactly one line through ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernhard Riemann
Georg Friedrich Bernhard Riemann (; 17 September 1826 – 20 July 1866) was a German mathematician who made contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the first rigorous formulation of the integral, the Riemann integral, and his work on Fourier series. His contributions to complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis. His 1859 paper on the prime-counting function, containing the original statement of the Riemann hypothesis, is regarded as a foundational paper of analytic number theory. Through his pioneering contributions to differential geometry, Riemann laid the foundations of the mathematics of general relativity. He is considered by many to be one of the greatest mathematicians of all time. Biography Early years Riemann was born on 17 September 1826 in Breselenz, a village near Dannenb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Felix Klein
Christian Felix Klein (; 25 April 1849 – 22 June 1925) was a German mathematician and mathematics educator, known for his work with group theory, complex analysis, non-Euclidean geometry, and on the associations between geometry and group theory. His 1872 Erlangen program, classifying geometries by their basic symmetry groups, was an influential synthesis of much of the mathematics of the time. Life Felix Klein was born on 25 April 1849 in Düsseldorf, to Prussian parents. His father, Caspar Klein (1809–1889), was a Prussian government official's secretary stationed in the Rhine Province. His mother was Sophie Elise Klein (1819–1890, née Kayser). He attended the Gymnasium in Düsseldorf, then studied mathematics and physics at the University of Bonn, 1865–1866, intending to become a physicist. At that time, Julius Plücker had Bonn's professorship of mathematics and experimental physics, but by the time Klein became his assistant, in 1866, Plücker's interest wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philosophical Transactions Of The Royal Society Of London
''Philosophical Transactions of the Royal Society'' is a scientific journal published by the Royal Society. In its earliest days, it was a private venture of the Royal Society's secretary. It was established in 1665, making it the first journal in the world exclusively devoted to science, and therefore also the world's longest-running scientific journal. It became an official society publication in 1752. The use of the word ''philosophical'' in the title refers to natural philosophy, which was the equivalent of what would now be generally called ''science''. Current publication In 1887 the journal expanded and divided into two separate publications, one serving the physical sciences ('' Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences'') and the other focusing on the life sciences ('' Philosophical Transactions of the Royal Society B: Biological Sciences''). Both journals now publish themed issues and issues resulting from pap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arthur Cayley
Arthur Cayley (; 16 August 1821 – 26 January 1895) was a prolific United Kingdom of Great Britain and Ireland, British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics. As a child, Cayley enjoyed solving complex maths problems for amusement. He entered Trinity College, Cambridge, where he excelled in Greek language, Greek, French language, French, German language, German, and Italian language, Italian, as well as mathematics. He worked as a lawyer for 14 years. He postulated the Cayley–Hamilton theorem—that every square matrix is a root of its own characteristic polynomial, and verified it for matrices of order 2 and 3. He was the first to define the concept of a group (mathematics), group in the modern way—as a set with a Binary function, binary operation satisfying certain laws. Formerly, when mathematicians spoke of "groups", they had meant permutation groups. Cayley tables and Cayley graphs as well as Cayle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |