|
Excitons
An exciton is a bound state of an electron and an electron hole which are attracted to each other by the electrostatic Coulomb force resulting from their opposite charges. It is an electrically neutral quasiparticle regarded as an elementary excitation primarily in condensed matter, such as insulators, semiconductors, some metals, and in some liquids. It transports energy without transporting net electric charge. An exciton can form when an electron from the valence band of a crystal is promoted in energy to the conduction band e.g., when a material absorbs a photon. Promoting the electron to the conduction band leaves a positively charged hole in the valence band. Here 'hole' represents the unoccupied quantum mechanical electron state with a positive charge, an analogue in crystal of a positron. Because of the attractive coulomb force between the electron and the hole, a bound state is formed, akin to that of the electron and proton in a hydrogen atom or the electron and pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exciton
An exciton is a bound state of an electron and an electron hole which are attracted to each other by the electrostatic Coulomb's law, Coulomb force resulting from their opposite charges. It is an electrically neutral quasiparticle regarded as an elementary excitation primarily in condensed matter, such as Electrical insulation, insulators, semiconductors, some metals, and in some liquids. It transports energy without transporting net electric charge. An exciton can form when an electron from the valence band of a crystal is promoted in energy to the conduction band e.g., when a material absorbs a photon. Promoting the electron to the conduction band leaves a positively charged hole in the valence band. Here 'hole' represents the unoccupied quantum mechanical electron state with a positive charge, an analogue in crystal of a positron. Because of the attractive coulomb force between the electron and the hole, a bound state is formed, akin to that of the electron and proton in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Organic Semiconductors
Organic semiconductors are solids whose building blocks are pi-bonded molecules or polymers made up by carbon and hydrogen atoms and – at times – heteroatoms such as nitrogen, sulfur and oxygen. They exist in the form of molecular crystals or amorphous thin films. In general, they are electrical insulators, but become semiconducting when charges are injected from appropriate electrodes or are introduced by doping or photoexcitation. General properties In molecular crystals the energetic separation between the top of the valence band and the bottom conduction band, i.e. the band gap, is typically 2.5–4 eV, while in inorganic semiconductors the band gaps are typically 1–2 eV. This implies that molecular crystals are, in fact, insulators rather than semiconductors in the conventional sense. They become semiconducting only when charge carriers are either injected from the electrodes or generated by intentional or unintentional doping. Charge carriers can also be g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Hole
In physics, chemistry, and electronic engineering, an electron hole (often simply called a hole) is a quasiparticle denoting the lack of an electron at a position where one could exist in an atom or crystal structure, atomic lattice. Since in a normal atom or crystal lattice the negative charge of the electrons is balanced by the positive charge of the atomic nucleus, atomic nuclei, the absence of an electron leaves a net positive charge at the hole's location. Holes in a metal or semiconductor crystal lattice can move through the lattice as electrons can, and act similarly to electric charge, positively-charged particles. They play an important role in the operation of semiconductor devices such as transistors, diodes (including light-emitting diodes) and integrated circuits. If an electron is excited into a higher state it leaves a hole in its old state. This meaning is used in Auger electron spectroscopy (and other x-ray techniques), in computational chemistry, and to explai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavefunction
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter), psi, respectively). Wave functions are complex number, complex-valued. For example, a wave function might assign a complex number to each point in a region of space. The Born rule provides the means to turn these complex probability amplitudes into actual probabilities. In one common form, it says that the squared modulus of a wave function that depends upon position is the probability density function, probability density of measurement in quantum mechanics, measuring a particle as being at a given place. The integral of a wavefunction's squared modulus over all the system's degrees of freedom must be equal to 1, a condition called ''normalization''. Since the wave function is complex-valued, only its relative phase and relative magnitud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bloch Theorem
In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential can be expressed as plane waves modulated by periodic functions. The theorem is named after the Swiss physicist Felix Bloch, who discovered the theorem in 1929. Mathematically, they are written where \mathbf is position, \psi is the wave function, u is a periodic function with the same periodicity as the crystal, the wave vector \mathbf is the crystal momentum vector, e is Euler's number, and i is the imaginary unit. Functions of this form are known as Bloch functions or Bloch states, and serve as a suitable basis for the wave functions or states of electrons in crystalline solids. The description of electrons in terms of Bloch functions, termed Bloch electrons (or less often ''Bloch Waves''), underlies the concept of electronic band structures. These eigenstates are written with subscripts as \psi_, where n is a discrete index, called the band index, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
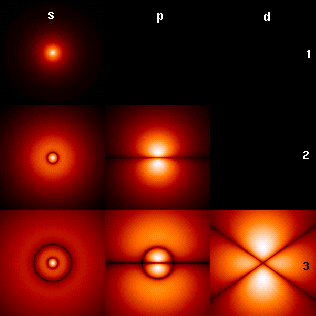
Hydrogen Atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral hydrogen atom contains a single positively charged proton in the nucleus, and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe. In everyday life on Earth, isolated hydrogen atoms (called "atomic hydrogen") are extremely rare. Instead, a hydrogen atom tends to combine with other atoms in compounds, or with another hydrogen atom to form ordinary (diatomic) hydrogen gas, H2. "Atomic hydrogen" and "hydrogen atom" in ordinary English use have overlapping, yet distinct, meanings. For example, a water molecule contains two hydrogen atoms, but does not contain atomic hydrogen (which would refer to isolated hydrogen atoms). Atomic spectroscopy shows that there is a discrete infinite set of states in which a hydrogen (or any) atom can exist, contrary to the predictions of classical physics. At ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binding Energy
In physics and chemistry, binding energy is the smallest amount of energy required to remove a particle from a system of particles or to disassemble a system of particles into individual parts. In the former meaning the term is predominantly used in condensed matter physics, atomic physics, and chemistry, whereas in nuclear physics the term '' separation energy'' is used. A bound system is typically at a lower energy level than its unbound constituents. According to relativity theory, a decrease in the total energy of a system is accompanied by a decrease in the total mass, where . Types There are several types of binding energy, each operating over a different distance and energy scale. The smaller the size of a bound system, the higher its associated binding energy. Mass–energy relation A bound system is typically at a lower energy level than its unbound constituents because its mass must be less than the total mass of its unbound constituents. For systems with low bi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relative Permittivity
The relative permittivity (in older texts, dielectric constant) is the permittivity of a material expressed as a ratio with the vacuum permittivity, electric permittivity of a vacuum. A dielectric is an insulating material, and the dielectric constant of an insulator measures the ability of the insulator to store electric energy in an electrical field. Permittivity is a material's property that affects the Coulomb force between two point charges in the material. Relative permittivity is the factor by which the electric field between the charges is decreased relative to vacuum. Likewise, relative permittivity is the ratio of the capacitance of a capacitor using that material as a dielectric, compared with a similar capacitor that has vacuum as its dielectric. Relative permittivity is also commonly known as the dielectric constant, a term still used but deprecated by standards organizations in engineering as well as in chemistry. Definition Relative permittivity is typically de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavevector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength), and its direction is perpendicular to the wavefront. In isotropic media, this is also the direction of wave propagation. A closely related vector is the angular wave vector (or angular wavevector), with a typical unit being radian per metre. The wave vector and angular wave vector are related by a fixed constant of proportionality, 2 radians per cycle. It is common in several fields of physics to refer to the angular wave vector simply as the ''wave vector'', in contrast to, for example, crystallography. It is also common to use the symbol for whichever is in use. In the context of special relativity, a ''wave four-vector'' can be defined, combining the (angular) wave vector and (angular) frequency. Definition The terms '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exchange Interaction
In chemistry and physics, the exchange interaction is a quantum mechanical constraint on the states of indistinguishable particles. While sometimes called an exchange force, or, in the case of fermions, Pauli repulsion, its consequences cannot always be predicted based on classical ideas of force. Both bosons and fermions can experience the exchange interaction. The wave function of identical particles, indistinguishable particles is subject to exchange symmetry: the wave function either changes sign (for fermions) or remains unchanged (for bosons) when two particles are exchanged. The exchange symmetry alters the Expectation value (quantum mechanics), expectation value of the distance between two indistinguishable particles when their wave functions overlap. For fermions the expectation value of the distance increases, and for bosons it decreases (compared to distinguishable particles). The exchange interaction arises from the combination of exchange symmetry and the Coulomb's l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reciprocal Lattice
Reciprocal lattice is a concept associated with solids with translational symmetry which plays a major role in many areas such as X-ray and electron diffraction as well as the energies of electrons in a solid. It emerges from the Fourier transform of the lattice associated with the arrangement of the atoms. The ''direct lattice'' or ''real lattice'' is a periodic function in physical space, such as a crystal system (usually a Bravais lattice). The reciprocal lattice exists in the mathematical space of spatial frequencies or wavenumbers ''k'', known as reciprocal space or ''k'' space; it is the dual of physical space considered as a vector space. In other words, the reciprocal lattice is the sublattice which is dual to the direct lattice. The reciprocal lattice is the set of all vectors \mathbf_m, that are wavevectors k of plane waves in the Fourier series of a spatial function whose periodicity is the same as that of a direct lattice \mathbf_n. Each plane wave in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fine Structure
In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to electron spin and relativistic corrections to the non-relativistic Schrödinger equation. It was first measured precisely for the hydrogen atom by Albert A. Michelson and Edward W. Morley in 1887, laying the basis for the theoretical treatment by Arnold Sommerfeld, introducing the fine-structure constant. Background Gross structure The ''gross structure'' of line spectra is the structure predicted by the quantum mechanics of non-relativistic electrons with no spin. For a hydrogenic atom, the gross structure energy levels only depend on the principal quantum number ''n''. However, a more accurate model takes into account relativistic and spin effects, which break the degeneracy of the energy levels and split the spectral lines. The scale of the fine structure splitting relative to the gross structure energies is on the order of (''Zα'')2, where ''Z'' is the atomic number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |