|
Effective Mass (spring–mass System)
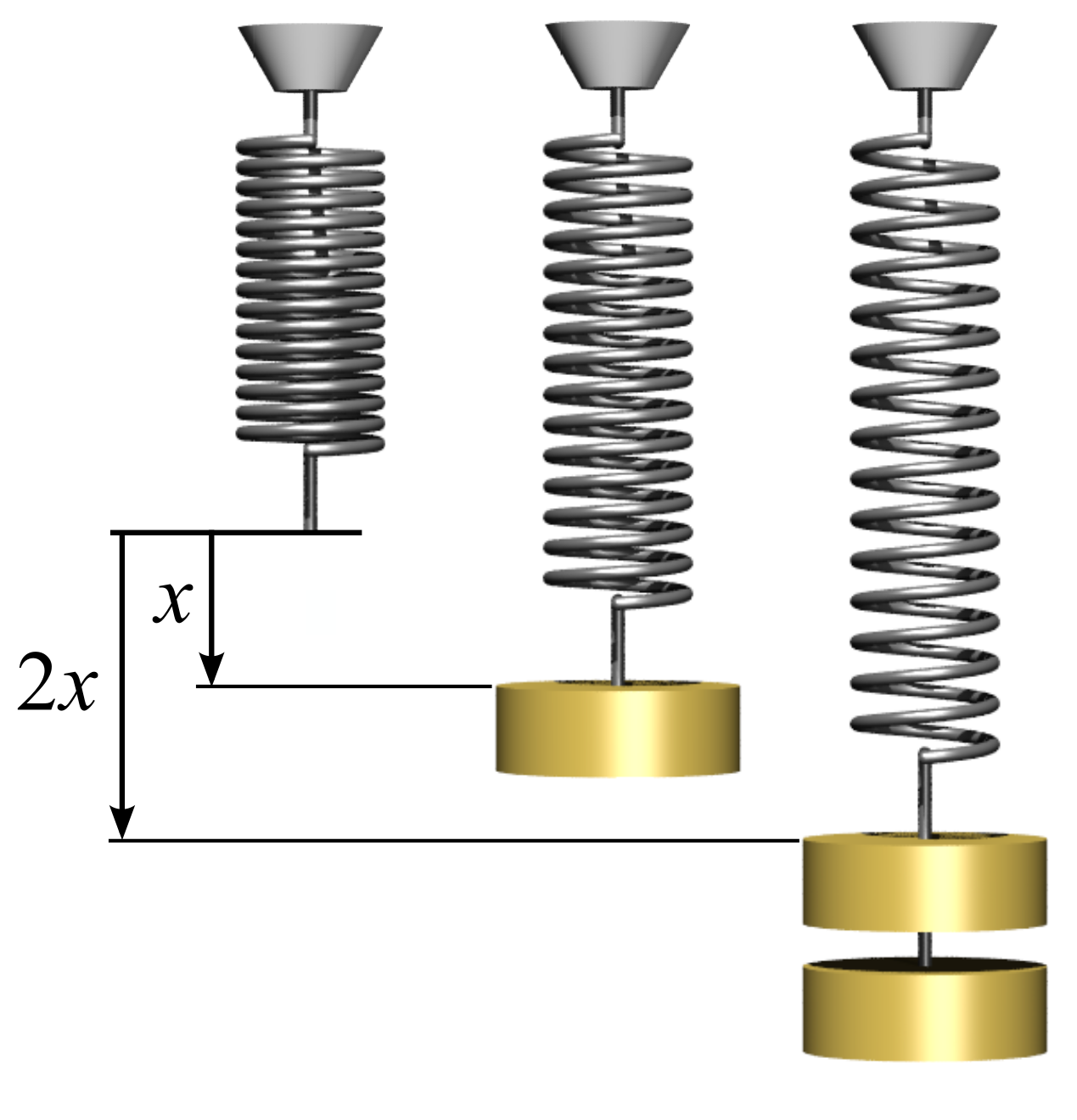
In a real spring–mass system, the spring has a non-negligible mass m. Since not all of the spring's length moves at the same velocity v as the suspended mass M (for example the point completely opposed to the mass M, at the other end of the spring, is not moving at all), its kinetic energy is ''not'' equal to \frac m v^2. As such, m cannot be simply added to M to determine the frequency of oscillation, and the effective mass of the spring, m_\mathrm, is defined as the mass that needs to be added to M to correctly predict the behavior of the system. Uniform spring (homogeneous) The effective mass of the spring in a spring–mass system when using a heavy spring (non-ideal) of uniform linear density is \frac of the mass of the spring and is independent of the direction of the spring–mass system (i.e., horizontal, vertical, and oblique systems all have the same effective mass). This is because external acceleration does not affect the period of motion around the equilibrium ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
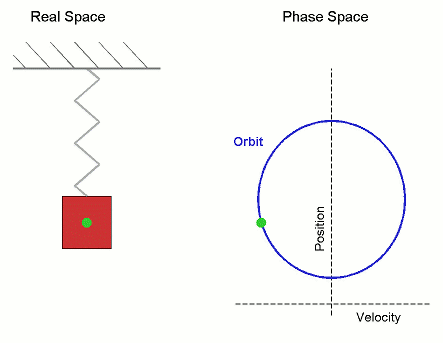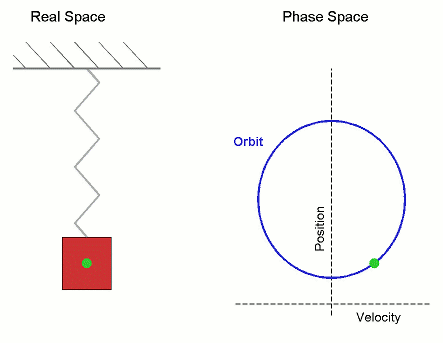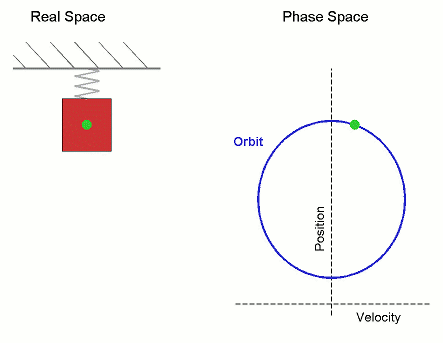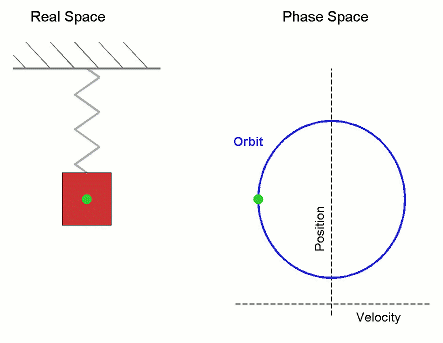
Simple Harmonic Motion
In mechanics and physics, simple harmonic motion (sometimes abbreviated as ) is a special type of periodic motion an object experiences by means of a restoring force whose magnitude is directly proportional to the distance of the object from an equilibrium position and acts towards the equilibrium position. It results in an oscillation that is described by a sinusoid which continues indefinitely (if uninhibited by friction or any other dissipation of energy). Simple harmonic motion can serve as a mathematical model for a variety of motions, but is typified by the oscillation of a mass on a spring when it is subject to the linear elastic restoring force given by Hooke's law. The motion is sinusoidal in time and demonstrates a single resonant frequency. Other phenomena can be modeled by simple harmonic motion, including the motion of a simple pendulum, although for it to be an accurate model, the net force on the object at the end of the pendulum must be proportional to the dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John William Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh ( ; 12 November 1842 – 30 June 1919), was an English physicist who received the Nobel Prize in Physics in 1904 "for his investigations of the densities of the most important gases and for his discovery of argon in connection with these studies". He served as president of the Royal Society from 1905 to 1908 and as chancellor of the University of Cambridge from 1908 to 1919. Rayleigh provided the first theoretical treatment of the elastic scattering of light by particles much smaller than the light's wavelength, a phenomenon now known as "Rayleigh scattering", which notably explains why the sky is blue. He studied and described transverse surface waves in solids, now known as "Rayleigh waves". He contributed extensively to fluid dynamics, with concepts such as the Rayleigh number (a dimensionless number associated with natural convection), Rayleigh flow, the Rayleigh–Taylor instability, and Rayleigh's criterion for the stability of Ta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduced Mass
In physics, reduced mass is a measure of the effective inertial mass of a system with two or more particles when the particles are interacting with each other. Reduced mass allows the two-body problem to be solved as if it were a one-body problem. Note, however, that the mass determining the gravitational force is ''not'' reduced. In the computation, one mass ''can'' be replaced with the reduced mass, if this is compensated by replacing the other mass with the sum of both masses. The reduced mass is frequently denoted by \mu ( mu), although the standard gravitational parameter is also denoted by \mu (as are a number of other physical quantities). It has the dimensions of mass, and SI unit kg. Reduced mass is particularly useful in classical mechanics. Equation Given two bodies, one with mass ''m''1 and the other with mass ''m''2, the equivalent one-body problem, with the position of one body with respect to the other as the unknown, is that of a single body of mass \m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
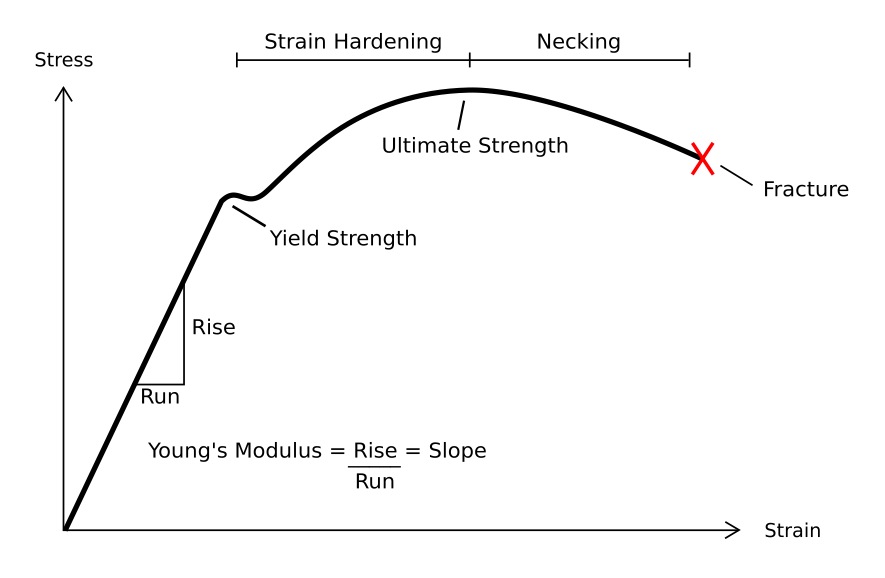
Elastic Deformation
In engineering, deformation (the change in size or shape of an object) may be ''elastic'' or ''plastic''. If the deformation is negligible, the object is said to be ''rigid''. Main concepts Occurrence of deformation in engineering applications is based on the following background concepts: * ''Displacements'' are any change in position of a point on the object, including whole-body translations and rotations ( rigid transformations). * ''Deformation'' are changes in the relative position between internals points on the object, excluding rigid transformations, causing the body to change shape or size. * ''Strain'' is the ''relative'' ''internal'' deformation, the dimensionless change in shape of an infinitesimal cube of material relative to a reference configuration. Mechanical strains are caused by mechanical stress, ''see stress-strain curve''. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spring Constant
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring (device), spring by some distance () Proportionality (mathematics)#Direct_proportionality, scales linearly with respect to that distance—that is, where is a constant factor characteristic of the spring (i.e., its stiffness), and is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660. Hooke's equation holds (to some extent) in many other situations where an elasticity (physics), elastic body is Deformation (physics), deformed, such as wind blowing on a tall building, and a musician plucking a string (music), string of a guitar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Delta Function
In mathematical analysis, the Dirac delta function (or distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Thus it can be Heuristic, represented heuristically as \delta (x) = \begin 0, & x \neq 0 \\ , & x = 0 \end such that \int_^ \delta(x) dx=1. Since there is no function having this property, modelling the delta "function" rigorously involves the use of limit (mathematics), limits or, as is common in mathematics, measure theory and the theory of distribution (mathematics), distributions. The delta function was introduced by physicist Paul Dirac, and has since been applied routinely in physics and engineering to model point masses and instantaneous impulses. It is called the delta function because it is a continuous analogue of the Kronecker delta function, which is usually defined on a discrete domain and takes values ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Initial Value Problem
In multivariable calculus, an initial value problem (IVP) is an ordinary differential equation together with an initial condition which specifies the value of the unknown function at a given point in the domain. Modeling a system in physics or other sciences frequently amounts to solving an initial value problem. In that context, the differential initial value is an equation which specifies how the system evolves with time given the initial conditions of the problem. Definition An initial value problem is a differential equation :y'(t) = f(t, y(t)) with f\colon \Omega \subset \mathbb \times \mathbb^n \to \mathbb^n where \Omega is an open set of \mathbb \times \mathbb^n, together with a point in the domain of f :(t_0, y_0) \in \Omega, called the initial condition. A solution to an initial value problem is a function y that is a solution to the differential equation and satisfies :y(t_0) = y_0. In higher dimensions, the differential equation is replaced with a family of eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Spring
A spring is a device consisting of an elastic but largely rigid material (typically metal) bent or molded into a form (especially a coil) that can return into shape after being compressed or extended. Springs can store energy when compressed. In everyday use, the term most often refers to coil springs, but there are many different spring designs. Modern springs are typically manufactured from spring steel. An example of a non-metallic spring is the bow, made traditionally of flexible yew wood, which when drawn stores energy to propel an arrow. When a conventional spring, without stiffness variability features, is compressed or stretched from its resting position, it exerts an opposing force approximately proportional to its change in length (this approximation breaks down for larger deflections). The ''rate'' or ''spring constant'' of a spring is the change in the force it exerts, divided by the change in deflection of the spring. That is, it is the gradient of the force ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being Derivative, differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the Graph of a function, graph of a given Function (mathematics), function between two points in the real line. Conventionally, areas above the horizontal Coordinate axis, axis of the plane are positive while areas below are n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spring (device)
A spring is a device consisting of an Elasticity (physics), elastic but largely rigid material (typically metal) bent or molded into a form (especially a coil) that can return into shape after being compressed or extended. Springs can Energy storage, store energy when compressed. In everyday use, the term most often refers to coil springs, but there are many different spring designs. Modern springs are typically manufactured from spring steel. An example of a non-metallic spring is the Bow (weapon), bow, made traditionally of flexible Taxus baccata, yew wood, which when Bow draw, drawn stores energy to propel an arrow. When a conventional spring, without stiffness variability features, is compressed or stretched from its resting position, it exerts an opposing force approximately proportional to its change in length (this approximation breaks down for larger deflections). The ''rate'' or ''spring constant'' of a spring is the change in the force it exerts, divided by the cha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Density
Linear density is the measure of a quantity of any characteristic value per unit of length. Linear mass density (titer in textile engineering, the amount of mass per unit length) and '' linear charge density'' (the amount of electric charge per unit length) are two common examples used in science and engineering. The term linear density or linear mass density is most often used when describing the characteristics of one-dimensional objects, although linear density can also be used to describe the density of a three-dimensional quantity along one particular dimension. Just as density is most often used to mean mass density, the term linear density likewise often refers to linear mass density. However, this is only one example of a linear density, as any quantity can be measured in terms of its value along one dimension. Linear mass density Consider a long, thin rod of mass M and length L. To calculate the average linear mass density, \bar\lambda_m, of this one dimensional obje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Harmonic Oscillator
In mechanics and physics, simple harmonic motion (sometimes abbreviated as ) is a special type of periodic function, periodic motion an object experiences by means of a restoring force whose magnitude is directly proportionality (mathematics), proportional to the distance of the object from an equilibrium position and acts towards the equilibrium position. It results in an oscillation that is described by a sinusoid which continues indefinitely (if uninhibited by friction or any other dissipation of energy). Simple harmonic motion can serve as a mathematical model for a variety of motions, but is typified by the oscillation of a mass on a spring (device), spring when it is subject to the linear elasticity (physics), elastic restoring force given by Hooke's law. The motion is sinusoidal in time and demonstrates a single resonance, resonant frequency. Other phenomena can be modeled by simple harmonic motion, including the motion of a pendulum, simple pendulum, although for it to b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |