|
Duality (mechanical Engineering)
In mechanical engineering, many terms are associated into pairs called duals. A dual of a relationship is formed by interchanging force (stress) and deformation (strain) in an expression. Here is a partial list of mechanical dualities: * force — deformation * stress — strain * stiffness method — flexibility method Examples Constitutive relation * stress and strain (Hooke's law.) :: \sigma = E \varepsilon \iff \varepsilon = \frac{E} \sigma \, See also * Duality (electrical circuits) * Hydraulic analogy * List of dualities * Series and parallel springs References * Fung, Y. C., ''A First Course in CONTINUUM MECHANICS'', 2nd edition, Prentice-Hall, Inc. 1977 Mechanical engineering Mechanical engineering Mechanical engineering is the study of physical machines that may involve force and movement. It is an engineering branch that combines engineering physics and mathematics principles with materials science, to design, analyze, manufactur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanical Engineering
Mechanical engineering is the study of physical machines that may involve force and movement. It is an engineering branch that combines engineering physics and mathematics principles with materials science, to design, analyze, manufacture, and maintain mechanical systems. It is one of the oldest and broadest of the engineering branches. Mechanical engineering requires an understanding of core areas including mechanics, dynamics, thermodynamics, materials science, structural analysis, and electricity. In addition to these core principles, mechanical engineers use tools such as computer-aided design (CAD), computer-aided manufacturing (CAM), and product lifecycle management to design and analyze manufacturing plants, industrial equipment and machinery, heating and cooling systems, transport systems, aircraft, watercraft, robotics, medical devices, weapons, and others. Mechanical engineering emerged as a field during the Industrial Revolution in Europe in the 18 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Force
A force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. The concept of force makes the everyday notion of pushing or pulling mathematically precise. Because the Magnitude (mathematics), magnitude and Direction (geometry, geography), direction of a force are both important, force is a Euclidean vector, vector quantity. The SI unit of force is the newton (unit), newton (N), and force is often represented by the symbol . Force plays an important role in classical mechanics. The concept of force is central to all three of Newton's laws of motion. Types of forces often encountered in classical mechanics include Elasticity (physics), elastic, frictional, Normal force, contact or "normal" forces, and gravity, gravitational. The rotational version of force is torque, which produces angular acceleration, changes in the rotational speed of an object. In an extended body, each part often applies forces on the adjacent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
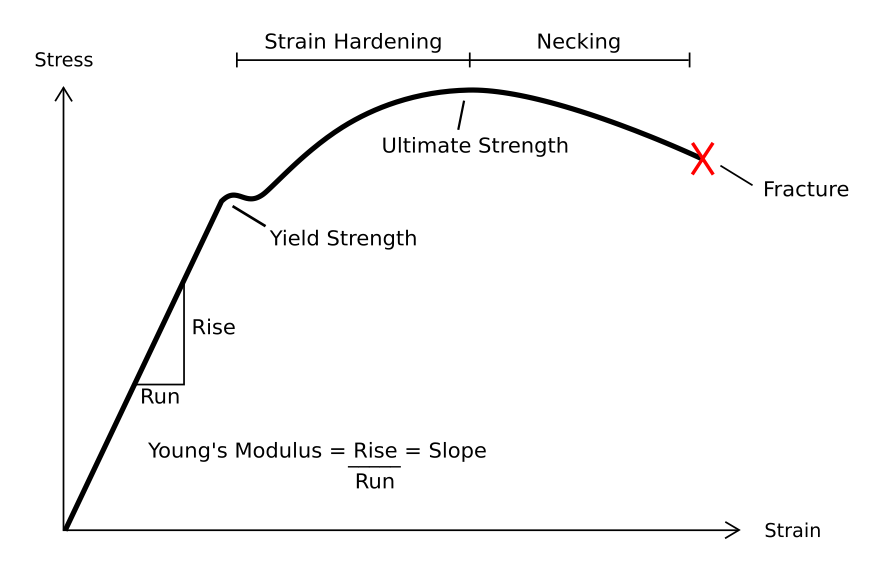
Deformation (engineering)
In engineering, deformation refers to the change in size or shape of an object. ''Displacements'' are the ''absolute'' change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain is the ''relative'' internal change in shape of an infinitesimally small cube of material and can be expressed as a non-dimensional change in length or angle of distortion of the cube. Strains are related to the forces acting on the cube, which are known as stress, by a stress-strain curve. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is elastic. The linear relationship for a material is known as Young's modulus. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation. The determination of the stress and strain throughout a solid object is given by the field of strength of materials and for a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (physics)
In continuum mechanics, stress is a physical quantity. It is a quantity that describes the magnitude of forces that cause deformation. Stress is defined as ''force per unit area''. When an object is pulled apart by a force it will cause elongation which is also known as deformation, like the stretching of an elastic band, it is called tensile stress. But, when the forces result in the compression of an object, it is called compressive stress. It results when forces like tension or compression act on a body. The greater this force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Therefore, stress is measured in newton per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushes o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strain (materials Science)
In physics, deformation is the continuum mechanics transformation of a body from a ''reference'' configuration to a ''current'' configuration. A configuration is a set containing the positions of all particles of the body. A deformation can occur because of external loads, intrinsic activity (e.g. muscle contraction), body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc. Strain is related to deformation in terms of ''relative'' displacement of particles in the body that excludes rigid-body motions. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body and on whether the metric tensor or its dual is considered. In a continuous body, a deformation field results from a stress field due to applied forces or because of some changes in the temperature field of the body. The re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stiffness Method
As one of the methods of structural analysis, the direct stiffness method, also known as the matrix stiffness method, is particularly suited for computer-automated analysis of complex structures including the statically indeterminate type. It is a ''matrix'' method that makes use of the members' stiffness relations for computing member forces and displacements in structures. The direct stiffness method is the most common implementation of the finite element method (FEM). In applying the method, the system must be modeled as a set of simpler, idealized elements interconnected at the nodes. The material stiffness properties of these elements are then, through matrix mathematics, compiled into a single matrix equation which governs the behaviour of the entire idealized structure. The structure’s unknown displacements and forces can then be determined by solving this equation. The direct stiffness method forms the basis for most commercial and free source finite element software. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flexibility Method
In structural engineering, the flexibility method, also called the method of consistent deformations, is the traditional method for computing member forces and displacements in structural systems. Its modern version formulated in terms of the members' flexibility matrices also has the name the matrix force method due to its use of member forces as the primary unknowns. Member flexibility Flexibility is the inverse of stiffness. For example, consider a spring that has ''Q'' and ''q'' as, respectively, its force and deformation: * The spring stiffness relation is ''Q = k q'' where ''k'' is the spring stiffness. * Its flexibility relation is ''q = f Q'', where ''f'' is the spring flexibility. * Hence, ''f'' = 1/''k''. A typical member flexibility relation has the following general form: where :''m'' = member number ''m''. :\mathbf^m = vector of member's characteristic deformations. :\mathbf^m = member flexibility matrix which characterises the member's susceptibility to defor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hooke's Law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of the spring (i.e., its stiffness), and is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660. Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, and a musician plucking a string of a guitar. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean. Hooke's law i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Duality (electrical Circuits)
In electrical engineering, electrical terms are associated into pairs called duals. A dual of a relationship is formed by interchanging voltage and current in an expression. The dual expression thus produced is of the same form, and the reason that the dual is always a valid statement can be traced to the duality of electricity and magnetism. Here is a partial list of electrical dualities: * voltage – current * parallel – serial (circuits) * resistance – conductance * voltage division – current division * impedance – admittance * capacitance – inductance * reactance – susceptance * short circuit – open circuit * Kirchhoff's current law – Kirchhoff's voltage law. * Thévenin's theorem – Norton's theorem History The use of duality in circuit theory is due to Alexander Russell who published his ideas in 1904.Alexander Russell, ''A Treatise on the Theory of Alternating Currents'', volume 1, chapter XXI, Camb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydraulic Analogy
The electronic–hydraulic analogy (derisively referred to as the drain-pipe theory by Oliver Lodge) is the most widely used analogy for "electron fluid" in a metal conductor. Since electric current is invisible and the processes in play in electronics are often difficult to demonstrate, the various electronic components are represented by hydraulic equivalents. Electricity (as well as heat) was originally understood to be a kind of fluid, and the names of certain electric quantities (such as current) are derived from hydraulic equivalents. As with all analogies, it demands an intuitive and competent understanding of the baseline paradigms (electronics and hydraulics), and in the case of the hydraulic analogy for electronics, students often have an inadequate knowledge of hydraulics. Paradigms There is no unique paradigm for establishing this analogy. Different paradigms have different strengths and weaknesses, depending on how and in what ways the intuitive understanding of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Dualities
Mathematics In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often (but not always) by means of an involution operation: if the dual of ''A'' is ''B'', then the dual of ''B'' is ''A''. * Alexander duality * Alvis–Curtis duality * Artin–Verdier duality * Beta-dual space * Coherent duality * De Groot dual * Dual abelian variety * Dual basis in a field extension * Dual bundle * Dual curve * Dual (category theory) * Dual graph * Dual group * Dual object * Dual pair * Dual polygon * Dual polyhedron * Dual problem * Dual representation * Dual q-Hahn polynomials * Dual q-Krawtchouk polynomials * Dual space * Dual topology * Dual wavelet * Duality (optimization) * Duality (order theory) * Duality of stereotype spaces * Duality (projective geometry) * Duality theory for distributive lattices * Dualizing complex * Dualizing sheaf * Eckma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series And Parallel Springs
In mechanics, two or more springs are said to be in series when they are connected end-to-end or point to point, and it is said to be in parallel when they are connected side-by-side; in both cases, so as to act as a single spring: More generally, two or more springs are ''in series'' when any external stress applied to the ensemble gets applied to each spring without change of magnitude, and the amount strain (deformation) of the ensemble is the sum of the strains of the individual springs. Conversely, they are said to be ''in parallel'' if the strain of the ensemble is their common strain, and the stress of the ensemble is the sum of their stresses. Any combination of Hookean (linear-response) springs in series or parallel behaves like a single Hookean spring. The formulas for combining their physical attributes are analogous to those that apply to capacitors connected in series or parallel in an electrical circuit. Formulas Equivalent spring The following table gives fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |