|
Dimension Reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable. Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics. Methods are commonly divided into linear and nonlinear approaches. Linear approaches can be further divided into feature selection and feature extraction. Dimensionality reduction can be used for noise reduction, data visualization, cluster analysis, or as an intermediate step to facilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intrinsic Dimension
The intrinsic dimension for a data set can be thought of as the minimal number of variables needed to represent the data set. Similarly, in signal processing of multidimensional signals, the intrinsic dimension of the signal describes how many variables are needed to generate a good approximation of the signal. When estimating intrinsic dimension, however, a slightly broader definition based on manifold dimension is often used, where a representation in the intrinsic dimension does only need to exist locally. Such intrinsic dimension estimation methods can thus handle data sets with different intrinsic dimensions in different parts of the data set. This is often referred to as local intrinsic dimensionality. The intrinsic dimension can be used as a lower bound of what dimension it is possible to compress a data set into through dimension reduction, but it can also be used as a measure of the complexity of the data set or signal. For a data set or signal of ''N'' variables, its int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
High-dimensional Space
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that was found nec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital Image Processing
Digital image processing is the use of a digital computer to process digital images through an algorithm. As a subcategory or field of digital signal processing, digital image processing has many advantages over analog image processing. It allows a much wider range of algorithms to be applied to the input data and can avoid problems such as the build-up of Noise (signal processing), noise and distortion during processing. Since images are defined over two dimensions (perhaps more), digital image processing may be modeled in the form of Multidimensional system, multidimensional systems. The generation and development of digital image processing are mainly affected by three factors: first, the development of computers; second, the development of mathematics (especially the creation and improvement of discrete mathematics, discrete mathematics theory); and third, the demand for a wide range of applications in environment, agriculture, military, industry and medical science has incre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-negative Matrix Factorization
Non-negative matrix factorization (NMF or NNMF), also non-negative matrix approximation is a group of algorithms in multivariate analysis and linear algebra where a matrix is factorized into (usually) two matrices and , with the property that all three matrices have no negative elements. This non-negativity makes the resulting matrices easier to inspect. Also, in applications such as processing of audio spectrograms or muscular activity, non-negativity is inherent to the data being considered. Since the problem is not exactly solvable in general, it is commonly approximated numerically. NMF finds applications in such fields as astronomy, computer vision, document clustering, missing data imputation, chemometrics, audio signal processing, recommender systems, and bioinformatics. History In chemometrics non-negative matrix factorization has a long history under the name "self modeling curve resolution". In this framework the vectors in the right matrix are continuous ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MIT Press
The MIT Press is the university press of the Massachusetts Institute of Technology (MIT), a private research university in Cambridge, Massachusetts. The MIT Press publishes a number of academic journals and has been a pioneer in the Open Access movement in academic publishing. History MIT Press traces its origins back to 1926 when MIT published a lecture series entitled ''Problems of Atomic Dynamics'' given by the visiting German physicist and later Nobel Prize winner, Max Born. In 1932, MIT's publishing operations were first formally instituted by the creation of an imprint called Technology Press. This imprint was founded by James R. Killian, Jr., at the time editor of MIT's alumni magazine and later to become MIT president. Technology Press published eight titles independently, then in 1937 entered into an arrangement with John Wiley & Sons in which Wiley took over marketing and editorial responsibilities. In 1961, the centennial of MIT's founding charter, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nature (journal)
''Nature'' is a British weekly scientific journal founded and based in London, England. As a multidisciplinary publication, ''Nature'' features Peer review, peer-reviewed research from a variety of academic disciplines, mainly in science and technology. It has core editorial offices across the United States, continental Europe, and Asia under the international scientific publishing company Springer Nature. ''Nature'' was one of the world's most cited scientific journals by the Science Edition of the 2022 ''Journal Citation Reports'' (with an ascribed impact factor of 50.5), making it one of the world's most-read and most prestigious academic journals. , it claimed an online readership of about three million unique readers per month. Founded in the autumn of 1869, ''Nature'' was first circulated by Norman Lockyer and Alexander MacMillan (publisher), Alexander MacMillan as a public forum for scientific innovations. The mid-20th century facilitated an editorial expansion for the j ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues And Eigenvectors
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative or complex number). Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation rotates, stretches, or shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with neither rotation nor shear. The corresponding eigenvalue is the factor by which an eigenvector is stretched or shrunk. If the eigenvalue is negative, the eigenvector's direction is reversed. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (: matrices) is a rectangle, rectangular array or table of numbers, symbol (formal), symbols, or expression (mathematics), expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " matrix", or a matrix of dimension . Matrices are commonly used in linear algebra, where they represent linear maps. In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotation (mathematics), rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation And Dependence
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in gen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one variable mainly correspond with greater values of the other variable, and the same holds for lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when greater values of one variable mainly correspond to lesser values of the other (that is, the variables tend to show opposite behavior), the covariance is negative. The magnitude of the covariance is the geometric mean of the variances that are in common for the two random variables. The Pearson product-moment correlation coefficient, correlation coefficient normalizes the covariance by dividing by the geometric mean of the total variances for the two random variables. A distinction must be made between (1) the covariance of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
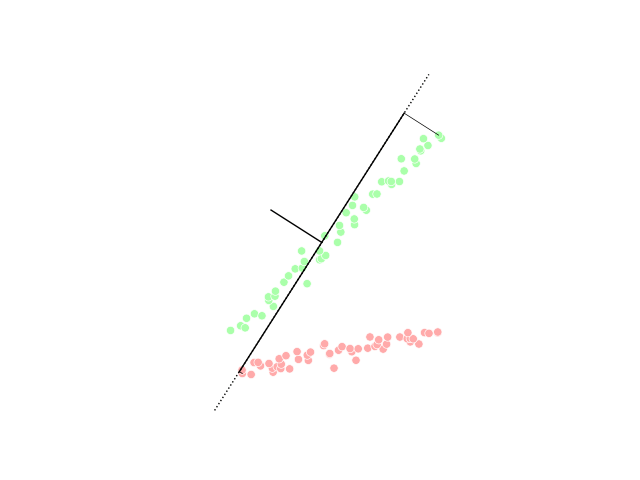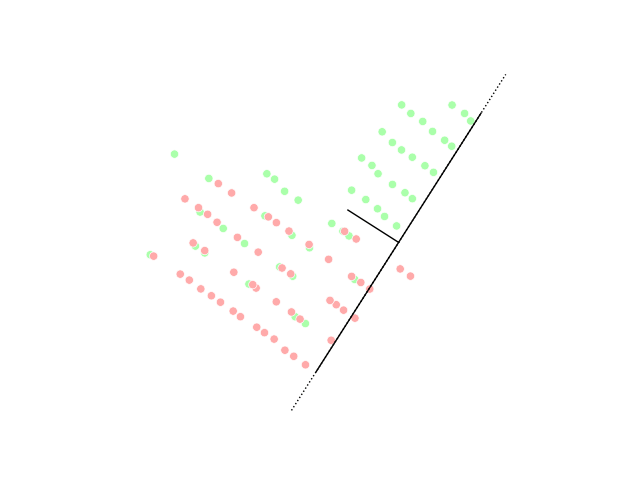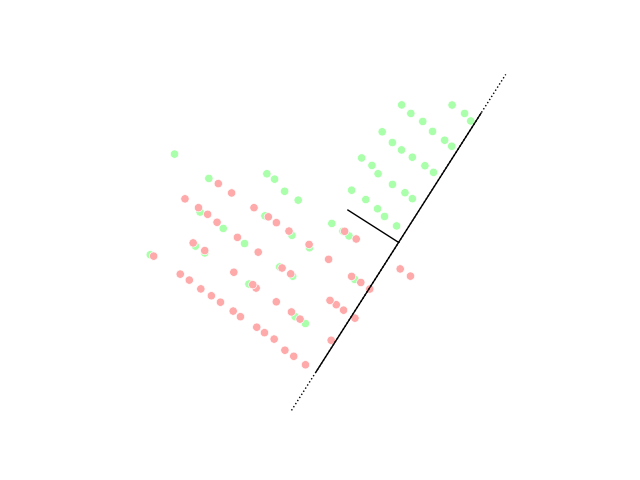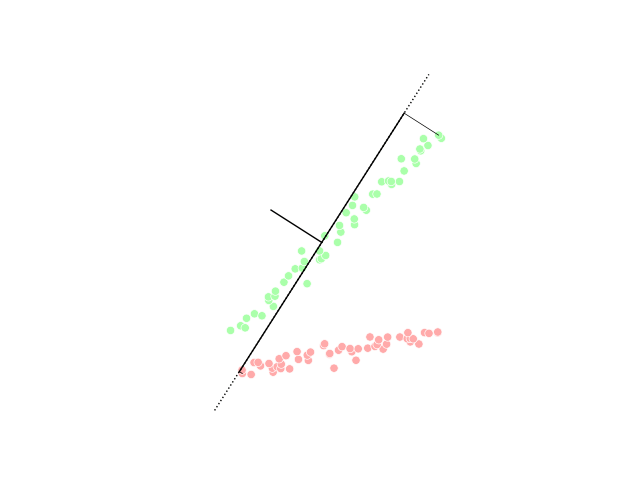
PCA Projection Illustration
PCA may refer to: Medicine and biology * Patient-controlled analgesia * Plate count agar in microbiology * Polymerase cycling assembly, for large DNA oligonucleotides * Posterior cerebral artery * Posterior cortical atrophy, a form of dementia *Prostate cancer * Protein-fragment complementation assay, to identify protein–protein interactions * Protocatechuic acid, a phenolic acid. * Personal Care Assistant, also known as unlicensed assistive personnel *Procainamide Military and government * EU-Armenia Partnership and Cooperation Agreement (PCA agreement between Armenia and the EU) * Parks Canada Agency * Partnership and Cooperation Agreement (EU) * Permanent change of assignment in US armed forces Organizations Business * Packaging Corporation of America * Peanut Corporation of America, former company * Pennsylvania Central Airlines 1936-1948 Education * Pacific Coast Academy, fictional school in TV series ''Zoey 101'' * Parents and citizens associations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
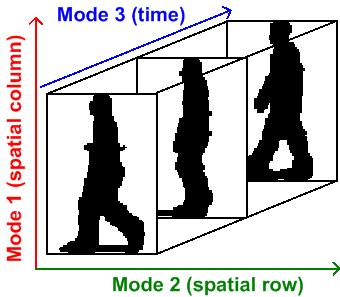
Multilinear Subspace Learning
Multilinear subspace learning is an approach for disentangling the causal factor of data formation and performing dimensionality reduction.M. A. O. Vasilescu, D. Terzopoulos (2003"Multilinear Subspace Analysis of Image Ensembles" "Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR’03), Madison, WI, June, 2003"M. A. O. Vasilescu, D. Terzopoulos (2002"Multilinear Analysis of Image Ensembles: TensorFaces" Proc. 7th European Conference on Computer Vision (ECCV'02), Copenhagen, Denmark, May, 2002M. A. O. Vasilescu,(2002"Human Motion Signatures: Analysis, Synthesis, Recognition" "Proceedings of International Conference on Pattern Recognition (ICPR 2002), Vol. 3, Quebec City, Canada, Aug, 2002, 456–460." The Dimensionality reduction can be performed on a data tensor that contains a collection of observations that have been vectorized, or observations that are treated as matrices and concatenated into a data tensor.X. He, D. Cai, P. NiyogiTensor s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |