|
Congruence (general Relativity)
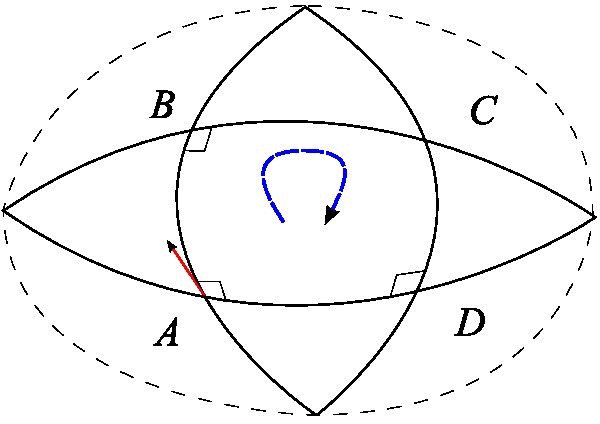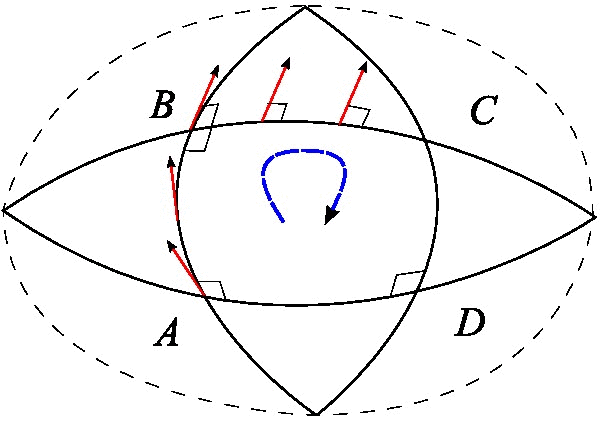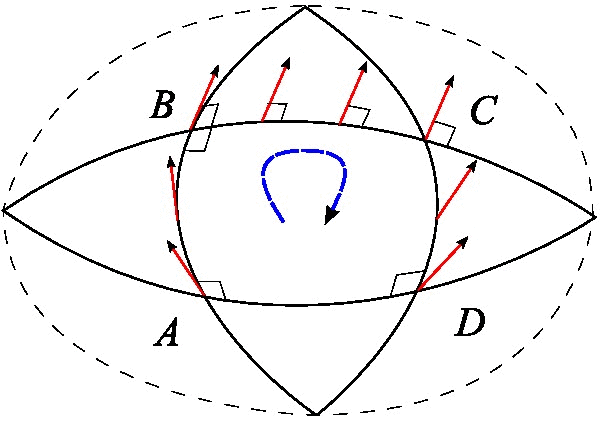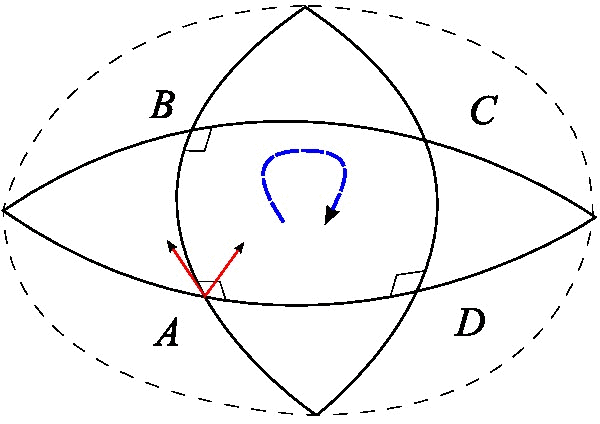
In general relativity, a congruence (more properly, a congruence of curves) is the set of integral curves of a (nowhere vanishing) vector field in a four-dimensional Lorentzian manifold which is interpreted physically as a model of spacetime. Often this manifold will be taken to be an exact or approximate solution to the Einstein field equation. Types of congruences Congruences generated by nowhere vanishing timelike, null, or spacelike vector fields are called ''timelike'', ''null'', or ''spacelike'' respectively. A congruence is called a ''geodesic congruence'' if it admits a tangent vector field \vec with vanishing covariant derivative, \nabla_ \vec = 0. Relation with vector fields The integral curves of the vector field are a family of ''non-intersecting'' parameterized curves which fill up the spacetime. The congruence consists of the curves themselves, without reference to a particular parameterization. Many distinct vector fields can give rise to the ''same'' congruen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the ' is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations. Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gravitat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Equation
The (two-way) wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields — as they occur in classical physics — such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light waves). It arises in fields like acoustics, electromagnetism, and fluid dynamics. Single mechanical or electromagnetic waves propagating in a pre-defined direction can also be described with the first-order one-way wave equation which is much easier to solve and also valid for inhomogenious media. Introduction The (two-way) wave equation is a second-order partial differential equation describing waves, including traveling and standing waves; the latter can be considered as linear superpositions of waves traveling in opposite directions. This article mostly focuses on the scalar wave equation describing waves in scalars by scalar functions of a time variable (a variable repres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Tensor
Shear may refer to: Textile production *Animal shearing, the collection of wool from various species **Sheep shearing *The removal of nap during wool cloth production Science and technology Engineering *Shear strength (soil), the shear strength of soil under loading *Shear line (locksmithing), where the inner cylinder ends and the outer cylinder begins in a cylinder lock *Shearing (manufacturing), a metalworking process which cuts stock without the formation of chips or the use of burning or melting *Shear (sheet metal), various tools to shear sheet metal *Board shear, in bookbinding, a tool to cut board or paper *Shear pin, in machinery, such as a plough, designed to shear (break) when a certain force is exceeded, to protect other components of the machine. *Shearing interferometer, in optics, a simple and very common means to check the collimation of beams by observing interference *Shearing in computer graphics, more commonly called screen tearing *Shear wall, a wall composed o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expansion Scalar
Expansion may refer to: Arts, entertainment and media * ''L'Expansion'', a French monthly business magazine * ''Expansion'' (album), by American jazz pianist Dave Burrell, released in 2004 * ''Expansions'' (McCoy Tyner album), 1970 * ''Expansions'' (Lonnie Liston Smith album), 1975 * ''Expansión'' (Mexico), a Mexican news portal linked to CNN * Expansion (sculpture) (2004) Bronze sculpture illuminated from within * ''Expansión'' (Spanish newspaper), a Spanish economic daily newspaper published in Spain * Expansion pack in gaming, extra content for games, often simply "expansion" Science, technology, and mathematics * Expansion (geometry), stretching of geometric objects with flat sides * Expansion (model theory), in mathematical logic, a mutual converse of a reduct * Expansion card, in computing, a printed circuit board that can be inserted into an expansion slot * Expansion chamber, on a two-stroke engine, a tuned exhaust system that enhances power output * Expansion joint, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Tensor
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold (i.e., it is a tensor field). It is a local invariant of Riemannian metrics which measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is ''flat'', i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection. It is a central mathematical tool in the theory of general relativity, the modern theory of gravity, and the curvature of spacetime is in principle observable via the geodesic deviation equation. The curvature tensor represents the tidal force experienced by a rigid body moving alo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Curvature Tensor
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold (i.e., it is a tensor field). It is a local invariant of Riemannian metrics which measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is ''flat'', i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection. It is a central mathematical tool in the theory of general relativity, the modern theory of gravity, and the curvature of spacetime is in principle observable via the geodesic deviation equation. The curvature tensor represents the tidal force experienced by a rigid body moving al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Foliation
In mathematics (differential geometry), a foliation is an equivalence relation on an ''n''-manifold, the equivalence classes being connected, injectively immersed submanifolds, all of the same dimension ''p'', modeled on the decomposition of the real coordinate space R''n'' into the cosets ''x'' + R''p'' of the standardly embedded subspace R''p''. The equivalence classes are called the leaves of the foliation. If the manifold and/or the submanifolds are required to have a piecewise-linear, differentiable (of class ''Cr''), or analytic structure then one defines piecewise-linear, differentiable, or analytic foliations, respectively. In the most important case of differentiable foliation of class ''Cr'' it is usually understood that ''r'' ≥ 1 (otherwise, ''C''0 is a topological foliation). The number ''p'' (the dimension of the leaves) is called the dimension of the foliation and is called its codimension. In some papers on general relativity by mathematical physicists, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Traceless
In linear algebra, the trace of a square matrix , denoted , is defined to be the sum of elements on the main diagonal (from the upper left to the lower right) of . The trace is only defined for a square matrix (). It can be proved that the trace of a matrix is the sum of its (complex) eigenvalues (counted with multiplicities). It can also be proved that for any two matrices and . This implies that similar matrices have the same trace. As a consequence one can define the trace of a linear operator mapping a finite-dimensional vector space into itself, since all matrices describing such an operator with respect to a basis are similar. The trace is related to the derivative of the determinant (see Jacobi's formula). Definition The trace of an square matrix is defined as \operatorname(\mathbf) = \sum_^n a_ = a_ + a_ + \dots + a_ where denotes the entry on the th row and th column of . The entries of can be real numbers or (more generally) complex numbers. The trace is not def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi–Walker Transport
Fermi–Walker transport is a process in general relativity used to define a coordinate system or reference frame such that all curvature in the frame is due to the presence of mass/energy density and not to arbitrary spin or rotation of the frame. Fermi–Walker differentiation In the theory of Lorentzian manifolds, Fermi–Walker differentiation is a generalization of covariant differentiation. In general relativity, Fermi–Walker derivatives of the spacelike vector fields in a frame field, taken with respect to the timelike unit vector field in the frame field, are used to define non-inertial and non-rotating frames, by stipulating that the Fermi–Walker derivatives should vanish. In the special case of inertial frames, the Fermi–Walker derivatives reduce to covariant derivatives. With a (-+++) sign convention, this is defined for a vector field ''X'' along a curve \gamma(s): :\frac=\frac - \left(X,\frac\right) V + (X,V)\frac, where is four-velocity, is the covariant der ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal
In mathematics, orthogonality is the generalization of the geometric notion of ''perpendicularity''. By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in other fields including art and chemistry. Etymology The word comes from the Ancient Greek ('), meaning "upright", and ('), meaning "angle". The Ancient Greek (') and Classical Latin ' originally denoted a rectangle. Later, they came to mean a right triangle. In the 12th century, the post-classical Latin word ''orthogonalis'' came to mean a right angle or something related to a right angle. Mathematics Physics * In optics, polarization states are said to be orthogonal when they propagate independently of each other, as in vertical and horizontal linear polarization or right- and left-handed circular polarization. * In special relativity, a time axis determined by a rapidity of motion is hyperbolic-orthogonal to a space axis of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection (linear Algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if it were applied once (i.e. P is idempotent). It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object. Definitions A projection on a vector space V is a linear operator P : V \to V such that P^2 = P. When V has an inner product and is complete (i.e. when V is a Hilbert space) the concept of orthogonality can be used. A projection P on a Hilbert space V is called an orthogonal projection if it satisfies \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P \mathbf y \rangle for all \mathbf x, \mathbf y \in V. A projection on a Hilbert ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
FRW Model
FRW may refer to: * FRW, currency symbol for the Rwandan franc * FRW metric, one name for an exact solution of Einstein's field equations of general relativity * Federation of Rural Workers, a former Irish trade union * Friction welding, a solid-state welding process * Front Row Wrestling, an American wrestling promotion * FRW, station code for the Fairwater railway station, Cardiff, Wales * FRW, SAME code for a fire warning in the United States * FRW, IATA airport code for Francistown Airport Phillip Gaonwe Matante International Airport , also known as Francistown International Airport, serves Francistown, Botswana. The airport is on the western edge of the city. Facilities The new terminal building opened in 2011 and the old termina ..., Botswana ** FRW, IATA airline designator for the defunct Bechuanaland National Airways based in Francistown {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |