|
Color Histogram
In image processing and photography, a color histogram is a representation of the distribution of colors in an image. For digital images, a color histogram represents the number of pixels that have colors in each of a fixed list of color ranges, that span the image's color space, the set of all possible colors. The color histogram can be built for any kind of color space, although the term is more often used for three-dimensional spaces like RGB or HSV. For monochromatic images, the term intensity histogram may be used instead. For multi-spectral images, where each pixel is represented by an arbitrary number of measurements (for example, beyond the three measurements in RGB), the color histogram is ''N''-dimensional, with N being the number of measurements taken. Each measurement has its own wavelength range of the light spectrum, some of which may be outside the visible spectrum. If the set of possible color values is sufficiently small, each of those colors may be placed on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Image Processing
An image is a visual representation of something. It can be two-dimensional, three-dimensional, or somehow otherwise feed into the visual system to convey information. An image can be an artifact, such as a photograph or other two-dimensional picture, that resembles a subject. In the context of signal processing, an image is a distributed amplitude of color(s). In optics, the term “image” may refer specifically to a 2D image. An image does not have to use the entire visual system to be a visual representation. A popular example of this is of a greyscale image, which uses the visual system's sensitivity to brightness across all wavelengths, without taking into account different colors. A black and white visual representation of something is still an image, even though it does not make full use of the visual system's capabilities. Images are typically still, but in some cases can be moving or animated. Characteristics Images may be two or three-dimensional, such as a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Odd-eyed Cat Histogram
Heterochromia is a variation in coloration. The term is most often used to describe color differences of the iris, but can also be applied to color variation of hair or skin. Heterochromia is determined by the production, delivery, and concentration of melanin (a pigment). It may be inherited, or caused by genetic mosaicism, chimerism, disease, or injury. It occurs in humans and certain breeds of domesticated animals. Heterochromia of the eye is called heterochromia iridum or heterochromia iridis. It can be complete or sectoral. In complete heterochromia, one iris is a different color from the other. In sectoral heterochromia, part of one iris is a different color from its remainder. In central heterochromia, there is a ring around the pupil or possibly spikes of different colors radiating from the pupil. Though multiple causes have been posited, the scientific consensus is that a lack of genetic diversity is the primary reason behind heterochromia, at least in domestic animals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
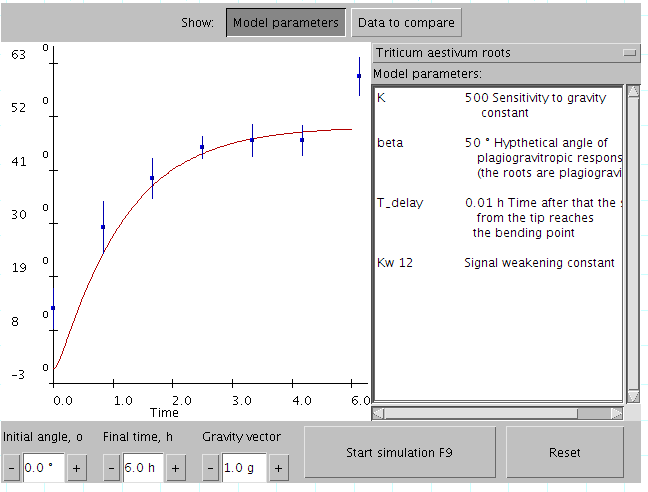
Java Applet
Java applets were small applications written in the Java programming language, or another programming language that compiles to Java bytecode, and delivered to users in the form of Java bytecode. The user launched the Java applet from a web page, and the applet was then executed within a Java virtual machine (JVM) in a process separate from the web browser itself. A Java applet could appear in a frame of the web page, a new application window, Sun's AppletViewer, or a stand-alone tool for testing applets. Java applets were introduced in the first version of the Java language, which was released in 1995. Beginning in 2013, major web browsers began to phase out support for the underlying technology applets used to run, with applets becoming completely unable to be run by 2015–2017. Java applets were deprecated by Java 9 in 2017. Java applets were usually written in Java, but other languages such as Jython, JRuby, Pascal, Scala, NetRexx, or Eiffel (via SmartEi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Function
In mathematical analysis, and applications in geometry, applied mathematics, engineering, and natural sciences, a function of a real variable is a function whose domain is the real numbers \mathbb, or a subset of \mathbb that contains an interval of positive length. Most real functions that are considered and studied are differentiable in some interval. The most widely considered such functions are the real functions, which are the real-valued functions of a real variable, that is, the functions of a real variable whose codomain is the set of real numbers. Nevertheless, the codomain of a function of a real variable may be any set. However, it is often assumed to have a structure of \mathbb-vector space over the reals. That is, the codomain may be a Euclidean space, a coordinate vector, the set of matrices of real numbers of a given size, or an \mathbb-algebra, such as the complex numbers or the quaternions. The structure \mathbb-vector space of the codomain induces a structur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lebesgue Measure
In measure theory, a branch of mathematics, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of ''n''-dimensional Euclidean space. For ''n'' = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called ''n''-dimensional volume, ''n''-volume, or simply volume. It is used throughout real analysis, in particular to define Lebesgue integration. Sets that can be assigned a Lebesgue measure are called Lebesgue-measurable; the measure of the Lebesgue-measurable set ''A'' is here denoted by ''λ''(''A''). Henri Lebesgue described this measure in the year 1901, followed the next year by his description of the Lebesgue integral. Both were published as part of his dissertation in 1902. Definition For any interval I = ,b/math>, or I = (a, b), in the set \mathbb of real numbers, let \ell(I)= b - a denote its length. For any subset E\subseteq\mathbb, the Lebesgue ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lp Space
In mathematics, the spaces are function spaces defined using a natural generalization of the -norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue , although according to the Bourbaki group they were first introduced by Frigyes Riesz . spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces. Because of their key role in the mathematical analysis of measure and probability spaces, Lebesgue spaces are used also in the theoretical discussion of problems in physics, statistics, economics, finance, engineering, and other disciplines. Applications Statistics In statistics, measures of central tendency and statistical dispersion, such as the mean, median, and standard deviation, are defined in terms of metrics, and measures of central tendency can be characterized as solutions to variational problems. In penalized regression, "L1 penalty" and "L2 penalty" refer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function Domain
In mathematics, the domain of a function is the set of inputs accepted by the function. It is sometimes denoted by \operatorname(f) or \operatornamef, where is the function. More precisely, given a function f\colon X\to Y, the domain of is . Note that in modern mathematical language, the domain is part of the definition of a function rather than a property of it. In the special case that and are both subsets of \R, the function can be graphed in the Cartesian coordinate system. In this case, the domain is represented on the -axis of the graph, as the projection of the graph of the function onto the -axis. For a function f\colon X\to Y, the set is called the codomain, and the set of values attained by the function (which is a subset of ) is called its range or image. Any function can be restricted to a subset of its domain. The restriction of f \colon X \to Y to A, where A\subseteq X, is written as \left. f \_A \colon A \to Y. Natural domain If a real function is g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Content-based Image Retrieval
Content-based image retrieval, also known as query by image content ( QBIC) and content-based visual information retrieval (CBVIR), is the application of computer vision techniques to the image retrieval problem, that is, the problem of searching for digital images in large databases (see this surveyContent-based Multimedia Information Retrieval: State of the Art and Challenges' (Original source, 404'''Content-based Multimedia Information Retrieval: State of the Art and Challenges'', Michael Lew, et al., ACM Transactions on Multimedia Computing, Communications, and Applications, pp. 1–19, 2006. for a scientific overview of the CBIR field). Content-based image retrieval is opposed to traditional concept-based approaches (see Concept-based image indexing). "Content-based" means that the search analyzes the contents of the image rather than the metadata such as keywords, tags, or descriptions associated with the image. The term "content" in this context might refer to colors, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlogram
In the analysis of data, a correlogram is a chart of correlation statistics. For example, in time series analysis, a plot of the sample autocorrelations r_h\, versus h\, (the time lags) is an autocorrelogram. If cross-correlation is plotted, the result is called a cross-correlogram. The correlogram is a commonly used tool for checking randomness in a data set. If random, autocorrelations should be near zero for any and all time-lag separations. If non-random, then one or more of the autocorrelations will be significantly non-zero. In addition, correlograms are used in the model identification stage for Box–Jenkins autoregressive moving average time series models. Autocorrelations should be near-zero for randomness; if the analyst does not check for randomness, then the validity of many of the statistical conclusions becomes suspect. The correlogram is an excellent way of checking for such randomness. In multivariate analysis, correlation matrices shown as color-ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |