|
Classical Fluid
Classical fluidsR. Balescu, ''Equilibrium and Nonequilibrium Statistical Mechanics'', (John Wiley, 1975) are systems of particles which retain a definite volume, and are at sufficiently high temperatures (compared to their Fermi energy) that quantum effects can be neglected. A system of hard spheres, interacting only by hard collisions (e.g., billiards, marbles), is a model classical fluid. Such a system is well described by the Percus–Yevik equation. Common liquids, e.g., liquid air, gasoline etc., are essentially mixtures of classical fluids. Electrolytes, molten salts, salts dissolved in water, are classical charged fluids. A classical fluid when cooled undergoes a freezing transition. On heating it undergoes an evaporation transition and becomes a classical gas that obeys Boltzmann statistics. A system of charged classical particles moving in a uniform positive neutralizing background is known as a one-component plasma (OCP). This is well described by the Hyper-netted chain ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi Energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy difference between the highest and lowest occupied single-particle states in a quantum system of non-interacting fermions at absolute zero temperature. In a Fermi gas, the lowest occupied state is taken to have zero kinetic energy, whereas in a metal, the lowest occupied state is typically taken to mean the bottom of the conduction band. The term "Fermi energy" is often used to refer to a different yet closely related concept, the Fermi ''level'' (also called electrochemical potential).The use of the term "Fermi energy" as synonymous with Fermi level (a.k.a. electrochemical potential) is widespread in semiconductor physics. For example:''Electronics (fundamentals And Applications)''by D. Chattopadhyay''Semiconductor Physics and Applications''by Balkanski and Wallis. There are a few key differences between the Fermi level and Fermi energy, at least as they are used in this article: * The Fermi energ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum
In physics, a quantum (plural quanta) is the minimum amount of any physical entity ( physical property) involved in an interaction. The fundamental notion that a physical property can be "quantized" is referred to as "the hypothesis of quantization". This means that the magnitude of the physical property can take on only discrete values consisting of integer multiples of one quantum. For example, a photon is a single quantum of light (or of any other form of electromagnetic radiation). Similarly, the energy of an electron bound within an atom is quantized and can exist only in certain discrete values. (Atoms and matter in general are stable because electrons can exist only at discrete energy levels within an atom.) Quantization is one of the foundations of the much broader physics of quantum mechanics. Quantization of energy and its influence on how energy and matter interact ( quantum electrodynamics) is part of the fundamental framework for understanding and describing nature. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hard Spheres
Hard spheres are widely used as model particles in the statistical mechanical theory of fluids and solids. They are defined simply as impenetrable spheres that cannot overlap in space. They mimic the extremely strong ("infinitely elastic bouncing") repulsion that atoms and spherical molecules experience at very close distances. Hard spheres systems are studied by analytical means, by molecular dynamics simulations, and by the experimental study of certain colloidal model systems. The hard-sphere system provides a generic model that explains the quasiuniversal structure and dynamics of simple liquids. Formal definition Hard spheres of diameter \sigma are particles with the following pairwise interaction potential: :V(\mathbf_1,\mathbf_2)=\left\{ \begin{matrix}0 & \mbox{if}\quad , \mathbf{r}_1-\mathbf{r}_2, \geq \sigma \\ \infty & \mbox{if}\quad, \mathbf{r}_1-\mathbf{r}_2, < \sigma \end{matrix} \right. where and are th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percus–Yevick Approximation
In statistical mechanics the Percus–Yevick approximation is a closure relation to solve the Ornstein–Zernike equation. It is also referred to as the Percus–Yevick equation. It is commonly used in fluid theory to obtain e.g. expressions for the radial distribution function. The approximation is named after Jerome K. Percus and George J. Yevick. Derivation The direct correlation function represents the direct correlation between two particles in a system containing ''N'' − 2 other particles. It can be represented by : c(r)=g_(r) - g_(r) \, where g_(r) is the radial distribution function, i.e. g(r)=\exp \beta w(r)/math> (with ''w''(''r'') the potential of mean force) and g_(r) is the radial distribution function without the direct interaction between pairs u(r) included; i.e. we write g_(r)=\exp \beta(w(r)-u(r))/math>. Thus we ''approximate'' ''c''(''r'') by : c(r)=e^- e^. \, If we introduce the function y(r)=e^g(r) into the approximation for ''c''(''r'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann
Ludwig Eduard Boltzmann (; 20 February 1844 – 5 September 1906) was an Austrian physicist and philosopher. His greatest achievements were the development of statistical mechanics, and the statistical explanation of the second law of thermodynamics. In 1877 he provided the current definition of entropy, S = k_ \ln \Omega \!, where Ω is the number of microstates whose energy equals the system's energy, interpreted as a measure of statistical disorder of a system. Max Planck named the constant the Boltzmann constant. Statistical mechanics is one of the pillars of modern physics. It describes how macroscopic observations (such as temperature and pressure) are related to microscopic parameters that fluctuate around an average. It connects thermodynamic quantities (such as heat capacity) to microscopic behavior, whereas, in classical thermodynamics, the only available option would be to measure and tabulate such quantities for various materials. Biography Childhood and educatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical-map Hypernetted-chain Method
The classical-map hypernetted-chain method (CHNC method) is a method used in many-body theoretical physics for interacting uniform electron liquids in two and three dimensions, and for non-ideal plasmas. The method extends the famous hypernetted-chain method (HNC) introduced by J. M. J van Leeuwen et al. to quantum fluids as well. The classical HNC, together with the Percus–Yevick approximation, are the two pillars which bear the brunt of most calculations in the theory of interacting classical fluids. Also, HNC and PY have become important in providing basic reference schemes in the theory of fluids, and hence they are of great importance to the physics of many-particle systems. The HNC and PY integral equations provide the pair distribution functions of the particles in a classical fluid, even for very high coupling strengths. The coupling strength is measured by the ratio of the potential energy to the kinetic energy. In a classical fluid, the kinetic energy is proportional ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Dynamics
Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamic "evolution" of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton's equations of motion for a system of interacting particles, where forces between the particles and their potential energies are often calculated using interatomic potentials or molecular mechanical force fields. The method is applied mostly in chemical physics, materials science, and biophysics. Because molecular systems typically consist of a vast number of particles, it is impossible to determine the properties of such complex systems analytically; MD simulation circumvents this problem by using numerical methods. However, long MD simulations are mathematically ill-conditioned, generating cumulative erro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Electron Model
In solid-state physics, the free electron model is a quantum mechanical model for the behaviour of charge carriers in a metallic solid. It was developed in 1927, principally by Arnold Sommerfeld, who combined the classical Drude model with quantum mechanical Fermi–Dirac statistics and hence it is also known as the Drude–Sommerfeld model. Given its simplicity, it is surprisingly successful in explaining many experimental phenomena, especially * the Wiedemann–Franz law which relates electrical conductivity and thermal conductivity; * the temperature dependence of the electron heat capacity; * the shape of the electronic density of states; * the range of binding energy values; * electrical conductivities; * the Seebeck coefficient of the thermoelectric effect; * thermal electron emission and field electron emission from bulk metals. The free electron model solved many of the inconsistencies related to the Drude model and gave insight into several other properties of metals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi Gas
An ideal Fermi gas is a state of matter which is an ensemble of many non-interacting fermions. Fermions are particles that obey Fermi–Dirac statistics, like electrons, protons, and neutrons, and, in general, particles with half-integer spin. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density, temperature, and the set of available energy states. The model is named after the Italian physicist Enrico Fermi. This physical model can be accurately applied to many systems with many fermions. Some key examples are the behaviour of charge carriers in a metal, nucleons in an atomic nucleus, neutrons in a neutron star, and electrons in a white dwarf. Description An ideal Fermi gas or free Fermi gas is a physical model assuming a collection of non-interacting fermions in a constant potential well. Fermions are elementary or composite particles with half-integer spin, thus follow F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Monte Carlo
Quantum Monte Carlo encompasses a large family of computational methods whose common aim is the study of complex quantum systems. One of the major goals of these approaches is to provide a reliable solution (or an accurate approximation) of the quantum many-body problem. The diverse flavors of quantum Monte Carlo approaches all share the common use of the Monte Carlo method to handle the multi-dimensional integrals that arise in the different formulations of the many-body problem. Quantum Monte Carlo methods allow for a direct treatment and description of complex many-body effects encoded in the wave function, going beyond mean-field theory. In particular, there exist numerically exact and polynomially-scaling algorithms to exactly study static properties of boson systems without geometrical frustration. For fermions, there exist very good approximations to their static properties and numerically exact exponentially scaling quantum Monte Carlo algorithms, but none that ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Path Integral Formulation
The path integral formulation is a description in quantum mechanics that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude. This formulation has proven crucial to the subsequent development of theoretical physics, because manifest Lorentz covariance (time and space components of quantities enter equations in the same way) is easier to achieve than in the operator formalism of canonical quantization. Unlike previous methods, the path integral allows one to easily change coordinates between very different canonical descriptions of the same quantum system. Another advantage is that it is in practice easier to guess the correct form of the Lagrangian of a theory, which naturally enters the path integrals (for interactions of a certain type, these are ''coordi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
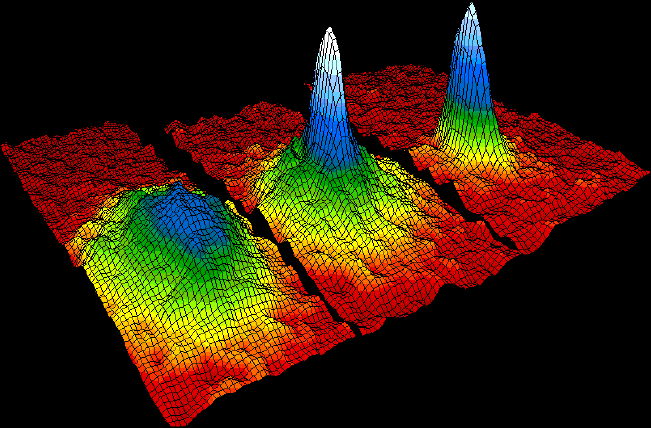
Bose–Einstein Condensate
In condensed matter physics, a Bose–Einstein condensate (BEC) is a state of matter that is typically formed when a gas of bosons at very low densities is cooled to temperatures very close to absolute zero (−273.15 °C or −459.67 °F). Under such conditions, a large fraction of bosons occupy the lowest quantum state, at which point microscopic quantum mechanical phenomena, particularly wavefunction interference, become apparent macroscopically. A BEC is formed by cooling a gas of extremely low density (about 100,000 times less dense than normal air) to ultra-low temperatures. This state was first predicted, generally, in 1924–1925 by Albert Einstein following and crediting a pioneering paper by Satyendra Nath Bose on the new field now known as quantum statistics. In 1995, the Bose-Einstein condensate was created by Eric Cornell and Carl Wieman of the University of Colorado at Boulder using rubidium atoms; later that year, Wolfgang Ketterle of MIT ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |