|
Cantor Pairing Function
In mathematics, a pairing function is a process to uniquely encode two natural numbers into a single natural number. Any pairing function can be used in set theory to prove that integers and rational numbers have the same cardinality as natural numbers. Definition A pairing function is a bijection :\pi:\mathbb \times \mathbb \to \mathbb. More generally, a pairing function on a set ''A'' is a function that maps each pair of elements from ''A'' into an element of ''A'', such that any two pairs of elements of ''A'' are associated with different elements of ''A,'' or a bijection from A^2 to ''A''. Hopcroft and Ullman pairing function Hopcroft and Ullman (1979) define the following pairing function: \langle i, j\rangle := \frac(i+j-2)(i+j-1) + i, where i, j\in\. This is the same as the Cantor pairing function below, shifted to exclude 0 (i.e., i=k_2+1, j=k_1+1, and \langle i, j\rangle - 1 = \pi(k_2,k_1)). Cantor pairing function The Cantor pairing function is a primitive recurs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is called the ''length'' of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an ''arbitrary'' index set. For example, (M, A, R, Y) is a sequence of letters with the letter 'M' first and 'Y' last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be '' finite'', as in these examples, or '' inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set Theory
Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory, as a branch of mathematics, is mostly concerned with those that are relevant to mathematics as a whole. The modern study of set theory was initiated by the German mathematicians Richard Dedekind and Georg Cantor in the 1870s. In particular, Georg Cantor is commonly considered the founder of set theory. The non-formalized systems investigated during this early stage go under the name of '' naive set theory''. After the discovery of paradoxes within naive set theory (such as Russell's paradox, Cantor's paradox and the Burali-Forti paradox) various axiomatic systems were proposed in the early twentieth century, of which Zermelo–Fraenkel set theory (with or without the axiom of choice) is still the best-known and most studied. Set theory is commonly employed as a foundational ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tarski's Theorem About Choice
In mathematics, Tarski's theorem, proved by , states that in ZF the theorem "For every infinite set A, there is a bijective map between the sets A and A\times A" implies the axiom of choice. The opposite direction was already known, thus the theorem and axiom of choice are equivalent. Tarski told that when he tried to publish the theorem in Comptes Rendus de l'Académie des Sciences Paris, Fréchet and Lebesgue refused to present it. Fréchet wrote that an implication between two well known propositions is not a new result. Lebesgue wrote that an implication between two false propositions is of no interest. Proof The goal is to prove that the axiom of choice is implied by the statement "for every infinite set A: , A, = , A \times A, ". It is known that the well-ordering theorem is equivalent to the axiom of choice; thus it is enough to show that the statement implies that for every set B there exists a well-order. Since the collection of all ordinals such that there exis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zermelo–Fraenkel Set Theory
In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in the early twentieth century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial axiom of choice (AC) included, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. Zermelo–Fraenkel set theory with the axiom of choice included is abbreviated ZFC, where C stands for "choice", and ZF refers to the axioms of Zermelo–Fraenkel set theory with the axiom of choice excluded. Informally, Zermelo–Fraenkel set theory is intended to formalize a single primitive notion, that of a hereditary well-founded set, so that all entities in the universe of discourse are such sets. Thus the axioms of Zermelo–Fraenkel set theory refer only to pure sets and prevent its models from conta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SK Combinator Calculus
The SKI combinator calculus is a combinatory logic, combinatory logic system and a model of computation, computational system. It can be thought of as a computer programming language, though it is not convenient for writing software. Instead, it is important in the mathematical theory of algorithms because it is an extremely simple Turing complete language. It can be likened to a reduced version of the untyped lambda calculus. It was introduced by Moses Schönfinkel and Haskell Curry. All operations in lambda calculus can be encoded via Combinatory logic#Completeness of the S-K basis, abstraction elimination into the SKI calculus as binary trees whose leaves are one of the three symbols S, K, and I (called ''combinators''). Notation Although the most formal representation of the objects in this system requires binary trees, for simpler typesetting they are often represented as parenthesized expressions, as a shorthand for the tree they represent. Any subtrees may be parenthesized ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least Significant Bit
In computing, bit numbering is the convention used to identify the bit positions in a binary number. Bit significance and indexing In computing, the least significant bit (LSB) is the bit position in a binary integer representing the binary 1s place of the integer. Similarly, the most significant bit (MSB) represents the highest-order place of the binary integer. The LSB is sometimes referred to as the ''low-order bit'' or ''right-most bit'', due to the convention in positional notation of writing less significant digits further to the right. The MSB is similarly referred to as the ''high-order bit'' or ''left-most bit''. In both cases, the LSB and MSB correlate directly to the least significant digit and most significant digit of a decimal integer. Bit indexing correlates to the positional notation of the value in base 2. For this reason, bit index is not affected by how the value is stored on the device, such as the value's byte order. Rather, it is a property of the n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
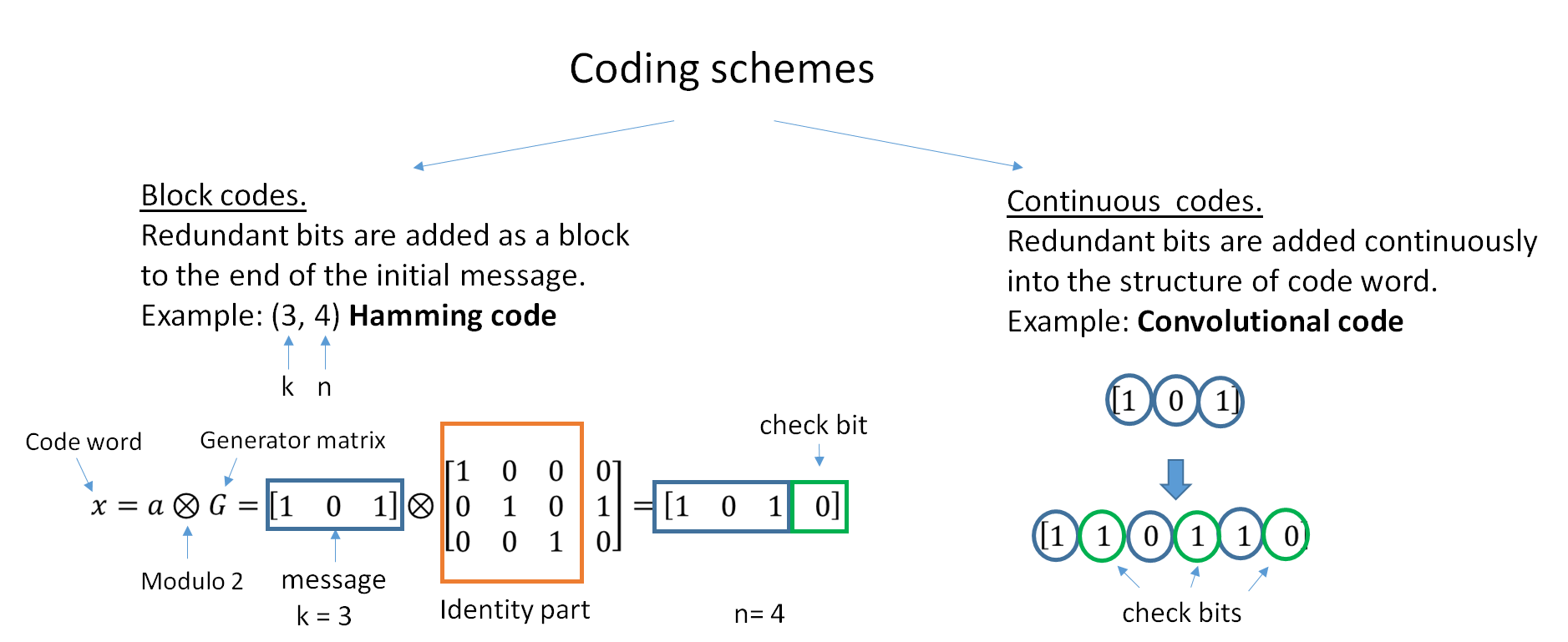
Bit-interleaving
In computing, telecommunication, information theory, and coding theory, an error correction code, sometimes error correcting code, (ECC) is used for controlling errors in data over unreliable or noisy communication channels. The central idea is the sender encodes the message with redundant information in the form of an ECC. The redundancy allows the receiver to detect a limited number of errors that may occur anywhere in the message, and often to correct these errors without retransmission. The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code. ECC contrasts with error detection in that errors that are encountered can be corrected, not simply detected. The advantage is that a system using ECC does not require a reverse channel to request retransmission of data when an error occurs. The downside is that there is a fixed overhead that is added to the message, thereby requiring a hig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Space
In computational complexity theory, L (also known as LSPACE or DLOGSPACE) is the complexity class containing decision problems that can be solved by a deterministic Turing machine using a logarithmic amount of writable memory space., Definition 8.12, p. 295., p. 177. Formally, the Turing machine has two tapes, one of which encodes the input and can only be read, whereas the other tape has logarithmic size but can be read as well as written. Logarithmic space is sufficient to hold a constant number of pointers into the input and a logarithmic number of boolean flags, and many basic logspace algorithms use the memory in this way. Complete problems and logical characterization Every non-trivial problem in L is complete under log-space reductions, so weaker reductions are required to identify meaningful notions of L-completeness, the most common being first-order reductions. A 2004 result by Omer Reingold shows that USTCON, the problem of whether there exists a p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Online Algorithm
In computer science, an online algorithm is one that can process its input piece-by-piece in a serial fashion, i.e., in the order that the input is fed to the algorithm, without having the entire input available from the start. In contrast, an offline algorithm is given the whole problem data from the beginning and is required to output an answer which solves the problem at hand. In operations research, the area in which online algorithms are developed is called online optimization. As an example, consider the sorting algorithms selection sort and insertion sort: selection sort repeatedly selects the minimum element from the unsorted remainder and places it at the front, which requires access to the entire input; it is thus an offline algorithm. On the other hand, insertion sort considers one input element per iteration and produces a partial solution without considering future elements. Thus insertion sort is an online algorithm. Note that the final result of an insertion sor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fast Multiplication
A multiplication algorithm is an algorithm (or method) to multiply two numbers. Depending on the size of the numbers, different algorithms are more efficient than others. Efficient multiplication algorithms have existed since the advent of the decimal system. Long multiplication If a positional numeral system is used, a natural way of multiplying numbers is taught in schools as long multiplication, sometimes called grade-school multiplication, sometimes called the Standard Algorithm: multiply the multiplicand by each digit of the multiplier and then add up all the properly shifted results. It requires memorization of the multiplication table for single digits. This is the usual algorithm for multiplying larger numbers by hand in base 10. A person doing long multiplication on paper will write down all the products and then add them together; an abacus-user will sum the products as soon as each one is computed. Example This example uses ''long multiplication'' to multiply 23,95 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Time
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is generally express ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |