|
Skew Arch Bridges
Skew may refer to: In mathematics * Skew lines, neither parallel nor intersecting. * Skew normal distribution, a probability distribution * Skew field or division ring * Skew-Hermitian matrix * Skew lattice * Skew polygon, whose vertices do not lie on a plane * Infinite skew polyhedron * Skew-symmetric graph * Skew-symmetric matrix * Skew tableau, a generalization of Young tableaux * Skewness, a measure of the asymmetry of a probability distribution * Shear mapping In science and technology *Skew, also synclinal or gauche in alkane stereochemistry *Skew ray (optics), an optical path not in a plane of symmetry * Skew arch, not at a right angle In computing * Clock skew * Transitive data skew, an issue of data synchronization In telecommunications * Skew (fax), unstraightness * Skew (antenna) a method to improve the horizontal radiation pattern Other uses * Volatility skew, in finance, a downward-sloping volatility smile * SKEW, the ticker symbol for the CBOE Skew Index Se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew Lines
In three-dimensional geometry, skew lines are two Line (geometry), lines that do not Line-line intersection, intersect and are not Parallel (geometry), parallel. A simple example of a pair of skew lines is the pair of lines through opposite edges of a regular tetrahedron. Two lines that both lie in the same plane must either cross each other or be parallel, so skew lines can exist only in three or more dimensions. Two lines are skew if and only if they are not coplanar. General position If four points are chosen at random Uniform distribution (continuous), uniformly within a unit cube, they will almost surely define a pair of skew lines. After the first three points have been chosen, the fourth point will define a non-skew line if, and only if, it is coplanar with the first three points. However, the plane through the first three points forms a subset of measure zero of the cube, and the probability that the fourth point lies on this plane is zero. If it does not, the lines defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Mapping
In plane geometry, a shear mapping is an affine transformation that displaces each point in a fixed direction by an amount proportional to its signed distance function, signed distance from a given straight line, line parallel (geometry), parallel to that direction. This type of mapping is also called shear transformation, transvection, or just shearing. The transformations can be applied with a shear matrix or transvection, an elementary matrix that represents the Elementary row operations#Row-addition transformations, addition of a multiple of one row or column to another. Such a matrix (mathematics), matrix may be derived by taking the identity matrix and replacing one of the zero elements with a non-zero value. An example is the linear map that takes any point with Cartesian coordinates, coordinates (x,y) to the point (x + 2y,y). In this case, the displacement is horizontal by a factor of 2 where the fixed line is the -axis, and the signed distance is the -coordinate. Not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volatility Smile
Volatility smiles are implied volatility patterns that arise in pricing financial options. It is a parameter (implied volatility) that is needed to be modified for the Black–Scholes formula to fit market prices. In particular for a given expiration, options whose strike price differs substantially from the underlying asset's price command higher prices (and thus implied volatilities) than what is suggested by standard option pricing models. These options are said to be either deep in-the-money or out-of-the-money. Graphing implied volatilities against strike prices for a given expiry produces a skewed "smile" instead of the expected flat surface. The pattern differs across various markets. Equity options traded in American markets did not show a volatility smile before the Crash of 1987 but began showing one afterwards. It is believed that investor reassessments of the probabilities of fat-tail have led to higher prices for out-of-the-money options. This anomaly implies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew (antenna)
Skew is a term used in antenna engineering. It is a technique to improve the horizontal radiation pattern of a high power transmitter station. In a high power VHF or UHF station, usually the antenna system is constructed to broadcast to four directions each separated 90° from each other. So the directivity of the antenna system resembles a four leaf clover. While settlements within the main lobe receive enough energy, the energy received by the settlements between the main lobes may be 6 dB less. One popular method to solve the problem is to skew the antenna panels symmetrically around the central axis of the mast.R.Busi: ''High altitude VHF and UHF Broadcasting stations'', EBU technical center, Brussels, 1967 p 25 Usually a skew of λ/4 gives the desired almost-uniform horizontal radiation pattern. But in cases where more than one RF signal is applied to antenna system (via combiner Power dividers (also power splitters and, when used in reverse, power combiners) and dire ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew (fax)
In fax systems, skew is the angular deviation of the received frame from rectangularity caused by asynchronism between the Image scanner, scanner and the recorder. This is the same as the angle between the scanning line, or recording line, and the perpendicular to the paper path. Skew is expressed numerically as the Trigonometric functions#tangent, tangent of the deviation angle. Skew detection and correction can be automatically applied by the receiving machine. References {{Use dmy dates, date=July 2019 Fax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
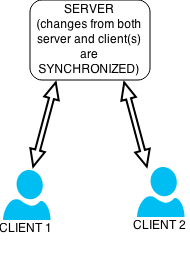
Transitive Data Skew
Data synchronization is the process of establishing consistency between source and target data stores, and the continuous harmonization of the data over time. It is fundamental to a wide variety of applications, including file synchronization and mobile device synchronization. Data synchronization can also be useful in encryption for synchronizing public key servers. Data synchronization is needed to update and keep multiple copies of a set of data coherent with one another or to maintain data integrity, Figure 3. For example, database replication is used to keep multiple copies of data synchronized with database servers that store data in different locations. Examples Examples include: * File synchronization, such as syncing a hand-held MP3 player to a desktop computer; * Cluster file systems, which are file systems that maintain data or indexes in a coherent fashion across a whole computing cluster; * Cache coherency, maintaining multiple copies of data in sync across multip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clock Skew
Clock skew (sometimes called timing skew) is a phenomenon in synchronous digital circuit systems (such as computer systems) in which the same sourced clock signal arrives at different components at different times due to gate or, in more advanced semiconductor technology, wire signal propagation delay. The instantaneous difference between the readings of any two clocks is called their skew. The operation of most digital circuits is synchronized by a periodic signal known as a " clock" that dictates the sequence and pacing of the devices on the circuit. This clock is distributed from a single source to all the memory elements of the circuit, which for example could be registers or flip-flops. In a circuit using edge-triggered registers, when the clock edge or tick arrives at a register, the register transfers the register input to the register output, and these new output values flow through combinational logic to provide the values at register inputs for the next clock tic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew Arch
A skew arch (also known as an oblique arch) is a method of construction that enables an arch bridge to span an obstacle at some angle other than a right angle. This results in the faces of the arch not being perpendicular to its abutments and its plan view being a parallelogram, rather than the rectangle that is the plan view of a regular, or "square" arch. In the case of a masonry skew arch, the construction requires precise stonemasonry, stonecutting, as the cuts do not form right angles, but once the principles were fully understood in the early 19th century, it became considerably easier and cheaper to build a skew arch of brick. The problem of building skew arch masonry bridges was addressed by a number of early civil engineers and mathematicians, including Giovanni Barbara (1726), William Chapman (engineer), William Chapman (1787), Benjamin Outram (1798), Peter Nicholson (architect), Peter Nicholson (1828), George Stephenson (1830), Edward Sang (1835), Charles Fox (civil a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ray (optics)
In optics, a ray is an idealized geometrical model of light or other electromagnetic radiation, obtained by choosing a curve that is perpendicular to the ''wavefronts'' of the actual light, and that points in the direction of energy flow. Rays are used to model the propagation of light through an optical system, by dividing the real light field up into discrete rays that can be computationally propagated through the system by the techniques of '' ray tracing''. This allows even very complex optical systems to be analyzed mathematically or simulated by computer. Ray tracing uses approximate solutions to Maxwell's equations that are valid as long as the light waves propagate through and around objects whose dimensions are much greater than the light's wavelength. '' Ray optics'' or ''geometrical optics'' does not describe phenomena such as diffraction, which require wave optics theory. Some wave phenomena such as interference can be modeled in limited circumstances by adding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alkane Stereochemistry
In chemistry, rotamers are chemical species that differ from one another primarily due to rotations about one or more single bonds. Various arrangements of atoms in a molecule that differ by rotation about single bonds can also be referred to as conformations. Conformers/rotamers differ little in their energies, so they are almost never separable in a practical sense. Rotations about single bonds are subject to small energy barriers. When the time scale for interconversion is long enough for isolation of individual rotamers (usually arbitrarily defined as a half-life of interconversion of 1000 seconds or longer), the species are termed atropisomers (''see:'' atropisomerism). The ring-flip of substituted cyclohexanes constitutes a common form of conformers. The study of the energetics of bond rotation is referred to as conformational analysis. In some cases, conformational analysis can be used to predict and explain product selectivity, mechanisms, and rates of reactions. Conform ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined. For a unimodal distribution (a distribution with a single peak), negative skew commonly indicates that the ''tail'' is on the left side of the distribution, and positive skew indicates that the tail is on the right. In cases where one tail is long but the other tail is fat, skewness does not obey a simple rule. For example, a zero value in skewness means that the tails on both sides of the mean balance out overall; this is the case for a symmetric distribution but can also be true for an asymmetric distribution where one tail is long and thin, and the other is short but fat. Thus, the judgement on the symmetry of a given distribution by using only its skewness is risky; the distribution shape must be taken into account. Introduction Consider the two d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew Normal Distribution
In probability theory and statistics, the skew normal distribution is a continuous probability distribution that generalises the normal distribution to allow for non-zero skewness. Definition Let \phi(x) denote the Normal distribution, standard normal probability density function :\phi(x)=\frace^ with the cumulative distribution function given by :\Phi(x) = \int_^ \phi(t)\ \mathrm dt = \frac \left[ 1 + \operatorname \left(\frac\right)\right], where "erf" is the error function. Then the probability density function (pdf) of the skew-normal distribution with parameter \alpha is given by :f(x) = 2\phi(x)\Phi(\alpha x). \, This distribution was first introduced by O'Hagan and Leonard (1976). Alternative forms to this distribution, with the corresponding quantile function, have been given by Ashour and Abdel-Hamid and by Mudholkar and Hutson. A stochastic process that underpins the distribution was described by Andel, Netuka and Zvara (1984). Both the distribution and its stochas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |