|
Fourier Series
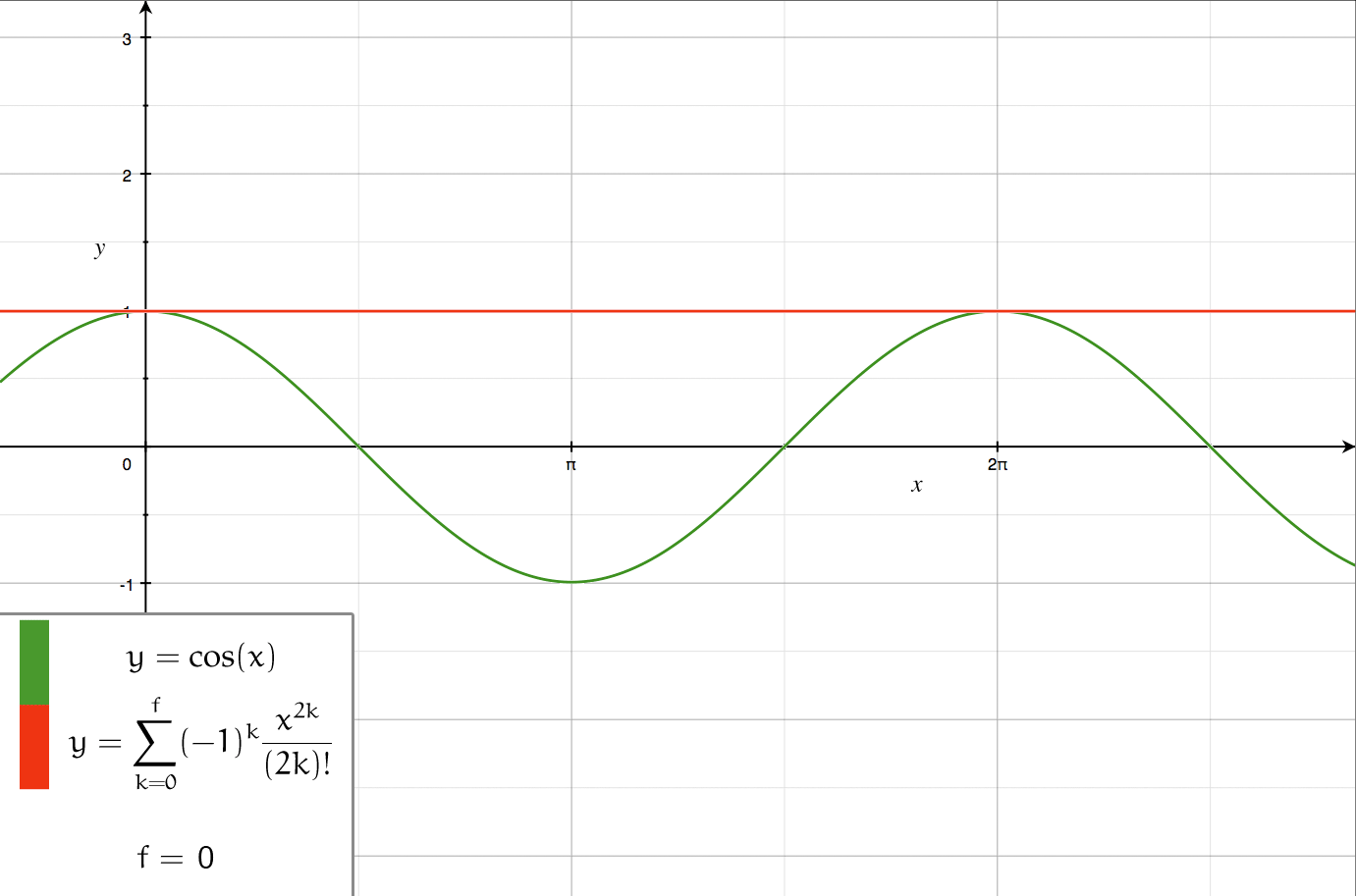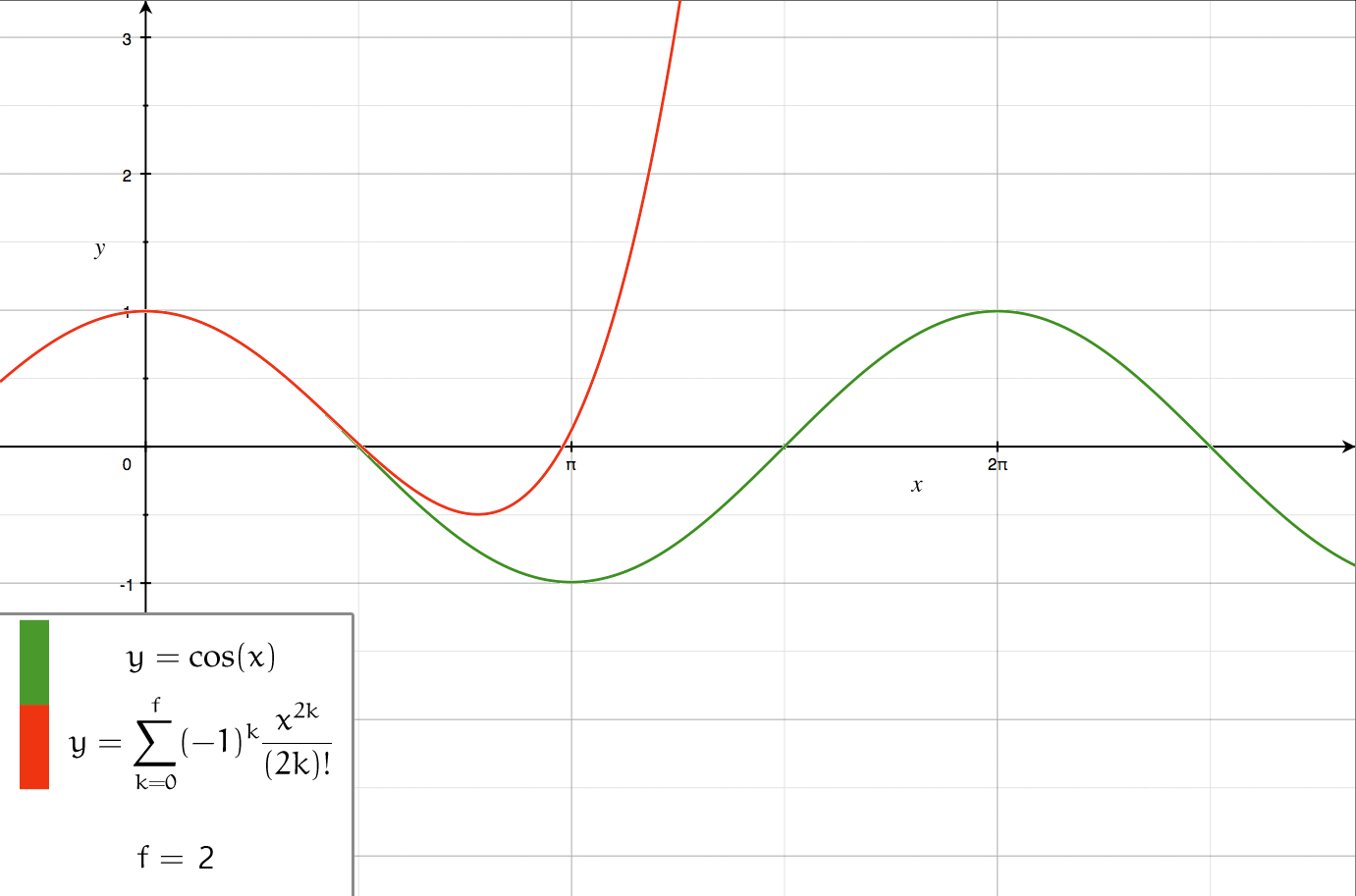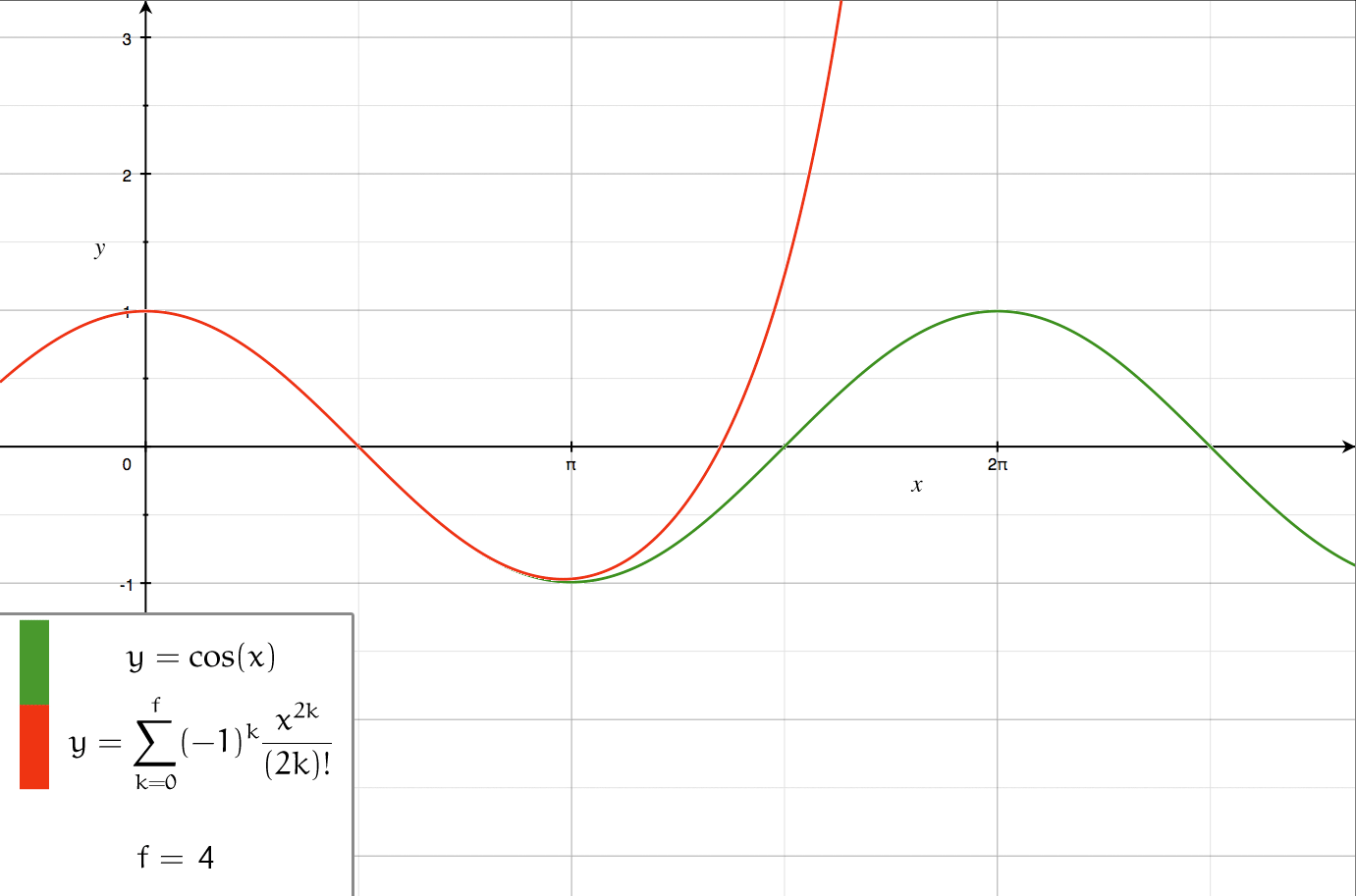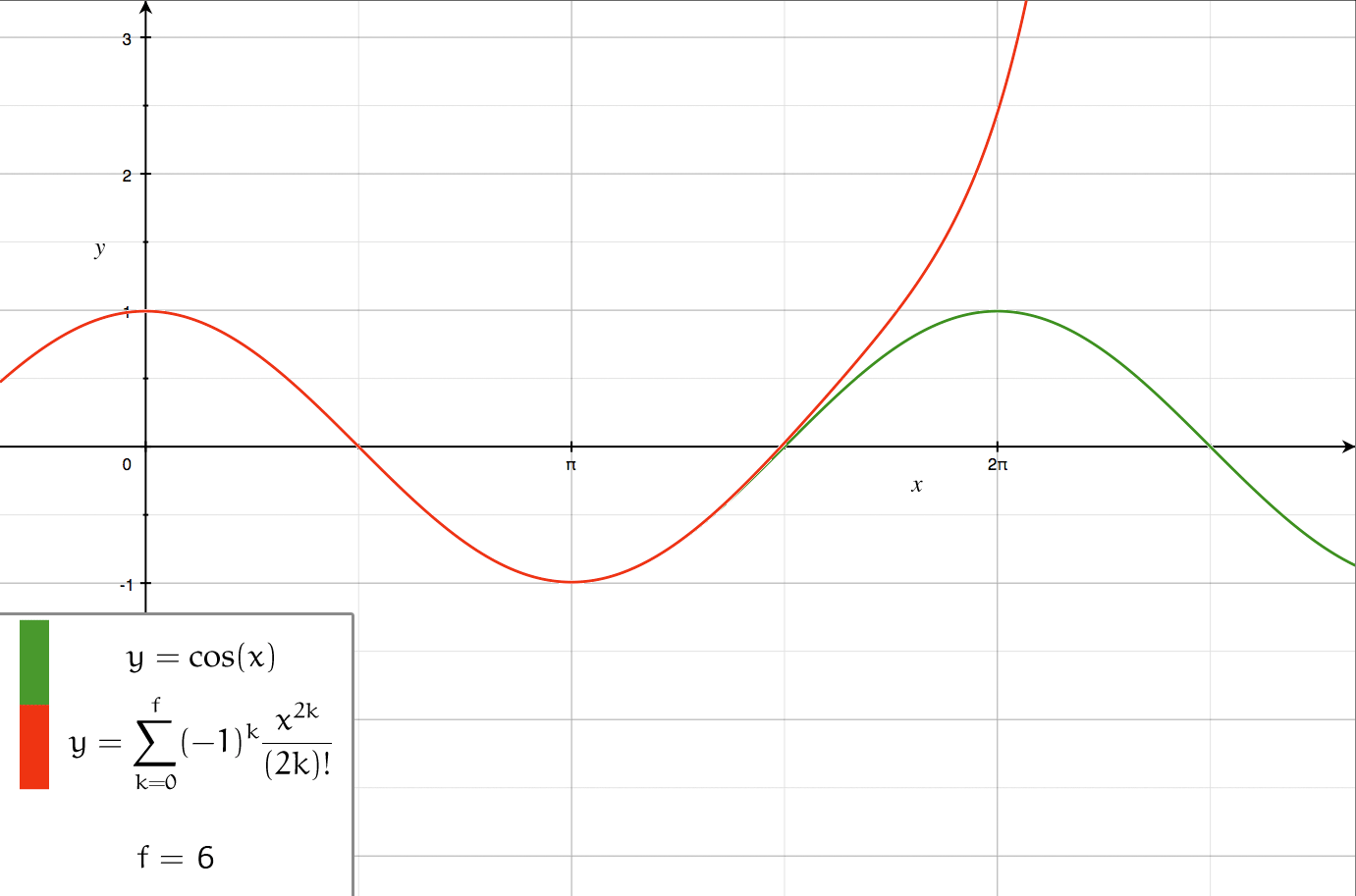
A Fourier series () is an Series expansion, expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series. By expressing a function as a sum of sines and cosines, many problems involving the function become easier to analyze because trigonometric functions are well understood. For example, Fourier series were first used by Joseph Fourier to find solutions to the heat equation. This application is possible because the derivatives of trigonometric functions fall into simple patterns. Fourier series cannot be used to approximate arbitrary functions, because most functions have infinitely many terms in their Fourier series, and the series do not always Convergent series, converge. Well-behaved functions, for example Smoothness, smooth functions, have Fourier series that converge to the original function. The coefficients of the Fourier series are determined by integrals of the function multiplied by trigonometric func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Wave (waveform)
A square wave is a non-sinusoidal waveform, non-sinusoidal periodic waveform in which the amplitude alternates at a steady frequency between fixed minimum and maximum values, with the same duration at minimum and maximum. In an ideal square wave, the transitions between minimum and maximum are instantaneous. The square wave is a special case of a pulse wave which allows arbitrary durations at minimum and maximum amplitudes. The ratio of the high period to the total period of a pulse wave is called the duty cycle. A true square wave has a 50% duty cycle (equal high and low periods). Square waves are often encountered in electronics and signal processing, particularly digital electronics and digital signal processing. Its stochastic counterpart is a two-state trajectory. Origin and uses Square waves are universally encountered in digital switching circuits and are naturally generated by binary (two-level) logic devices. They are used as timing references or "clock signa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Series Expansion
In mathematics, a series expansion is a technique that expresses a Function (mathematics), function as an infinite sum, or Series (mathematics), series, of simpler functions. It is a method for calculating a Function (mathematics), function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division). The resulting so-called ''Series (mathematics), series'' often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non-analytic functions. Types of series expansions There are several kinds of series expansions, listed below. Taylor series A ''Taylor series'' is a power ser ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Areas Of Mathematics
Mathematics is a broad subject that is commonly divided in many areas or branches that may be defined by their objects of study, by the used methods, or by both. For example, analytic number theory is a subarea of number theory devoted to the use of methods of analysis for the study of natural numbers. This glossary is alphabetically sorted. This hides a large part of the relationships between areas. For the broadest areas of mathematics, see . The Mathematics Subject Classification is a hierarchical list of areas and subjects of study that has been elaborated by the community of mathematicians. It is used by most publishers for classifying mathematical articles and books. A B C D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives. The function is often thought of as an "unknown" that solves the equation, similar to how is thought of as an unknown number solving, e.g., an algebraic equation like . However, it is usually impossible to write down explicit formulae for solutions of partial differential equations. There is correspondingly a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity and stability. Among the many open questions are the existence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler's Equation
In orbital mechanics, Kepler's equation relates various geometric properties of the orbit of a body subject to a central force. It was derived by Johannes Kepler in 1609 in Chapter 60 of his ''Astronomia nova'', and in book V of his ''Epitome of Copernican Astronomy'' (1621) Kepler proposed an iterative solution to the equation. This equation and its solution, however, first appeared in a 9th-century work by Habash al-Hasib al-Marwazi, which dealt with problems of parallax. The equation has played an important role in the history of both physics and mathematics, particularly classical celestial mechanics. Equation Kepler's equation is where M is the mean anomaly, E is the eccentric anomaly, and e is the Eccentricity (mathematics), eccentricity. The 'eccentric anomaly' E is useful to compute the position of a point moving in a Keplerian orbit. As for instance, if the body passes the periastron at coordinates x = a(1 - e), y = 0, at time t = t_0, then to find out the position ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Friedrich Wilhelm Bessel
Friedrich Wilhelm Bessel (; 22 July 1784 – 17 March 1846) was a German astronomer, mathematician, physicist, and geodesist. He was the first astronomer who determined reliable values for the distance from the Sun to another star by the method of parallax. Certain important mathematical functions were first studied systematically by Bessel and were named Bessel functions in his honour. Life and family Bessel was born in Minden, Westphalia, then capital of the Prussian administrative region Minden-Ravensberg, as second son of a civil servant into a large family. At the age of 14 he left the school, because he did not like the education in Latin language, and apprenticed in the import-export concern Kulenkamp at Bremen. The business's reliance on cargo ships led him to turn his mathematical skills to problems in navigation. This in turn led to an interest in astronomy as a way of determining longitude. Bessel came to the attention of Heinrich Wilhelm Olbers, a practising phy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deferent And Epicycle
In the Hipparchian, Ptolemaic, and Copernican systems of astronomy, the epicycle (, meaning "circle moving on another circle") was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets. In particular it explained the apparent retrograde motion of the five planets known at the time. Secondarily, it also explained changes in the apparent distances of the planets from the Earth. It was first proposed by Apollonius of Perga at the end of the 3rd century BC. It was developed by Apollonius of Perga and Hipparchus of Rhodes, who used it extensively, during the 2nd century BC, then formalized and extensively used by Ptolemy in his 2nd century AD astronomical treatise the '' Almagest''. Epicyclical motion is used in the Antikythera mechanism, itation requested/sup> an ancient Greek astronomical device, for compensating for the elliptical orbit of the Moon, moving faster at perigee and slower at apogee than cir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Académie Française
An academy (Attic Greek: Ἀκαδήμεια; Koine Greek Ἀκαδημία) is an institution of tertiary education. The name traces back to Plato's school of philosophy, founded approximately 386 BC at Akademia, a sanctuary of Athena, the goddess of wisdom and Skills, skill, north of Ancient Athens, Athens, Greece. The Royal Spanish Academy defines academy as scientific, literary or artistic society established with public authority and as a teaching establishment, public or private, of a professional, artistic, technical or simply practical nature. Etymology The word comes from the ''Academy'' in ancient Greece, which derives from the Athenian hero, ''Akademos''. Outside the city walls of Athens, the Gymnasium (ancient Greece), gymnasium was made famous by Plato as a center of learning. The sacred space, dedicated to the goddess of wisdom, Athena, had formerly been an olive Grove (nature), grove, hence the expression "the groves of Academe". In these gardens, the philos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Piecewise
In mathematics, a piecewise function (also called a piecewise-defined function, a hybrid function, or a function defined by cases) is a function whose domain is partitioned into several intervals ("subdomains") on which the function may be defined differently. Piecewise definition is actually a way of specifying the function, rather than a characteristic of the resulting function itself, as every function whose domain contains at least two points can be rewritten as a piecewise function. The first three paragraphs of this article only deal with this first meaning of "piecewise". Terms like piecewise linear, piecewise smooth, piecewise continuous, and others are also very common. The meaning of a function being piecewise P, for a property P is roughly that the domain of the function can be partitioned into pieces on which the property P holds, but is used slightly differently by different authors. Unlike the first meaning, this is a property of the function itself and not on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mémoire Sur La Propagation De La Chaleur Dans Les Corps Solides
This is a list of publications in mathematics, organized by field. Some reasons a particular publication might be regarded as important: *Topic creator – A publication that created a new topic *Breakthrough – A publication that changed scientific knowledge significantly *Influence – A publication which has significantly influenced the world or has had a massive impact on the teaching of mathematics. Among published compilations of important publications in mathematics are ''Landmark writings in Western mathematics 1640–1940'' by Ivor Grattan-Guinness and ''A Source Book in Mathematics'' by David Eugene Smith. Algebra Theory of equations '' Baudhayana Sulba Sutra'' * Baudhayana (8th century BCE) With linguistic evidence suggesting this text to have been written between the 8th and 5th centuries century BCE, this is one of the oldest mathematical texts. It laid the foundations of Indian mathematics and was influential in South Asia. It was primarily ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler–Bernoulli Beam Theory
Euler–Bernoulli beam theory (also known as engineer's beam theory or classical beam theory) is a simplification of the linear elasticity, linear theory of elasticity which provides a means of calculating the load-carrying and Deflection (engineering), deflection characteristics of Beam (structure), beams. It covers the case corresponding to small deflections of a beam (structure), beam that is subjected to lateral loads only. By ignoring the effects of shear deformation and rotatory inertia, it is thus a special case of Timoshenko–Ehrenfest beam theory. It was first enunciated circa 1750, but was not applied on a large scale until the development of the Eiffel Tower and the Ferris wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of the Second Industrial Revolution. Additional mathematical models have been developed, such as plate theory, but the simplicity of beam theory makes it an importa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Equation
The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light waves). It arises in fields like acoustics, electromagnetism, and fluid dynamics. This article focuses on waves in classical physics. Quantum physics uses an operator-based wave equation often as a relativistic wave equation. Introduction The wave equation is a hyperbolic partial differential equation describing waves, including traveling and standing waves; the latter can be considered as linear superpositions of waves traveling in opposite directions. This article mostly focuses on the scalar wave equation describing waves in scalars by scalar functions of a time variable (a variable representing time) and one or more spatial variables (variables representing a position in a space under discussion). At the same time, there a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |