|
Deltahedra
A deltahedron is a polyhedron whose faces are all equilateral triangles. The deltahedron was named by Martyn Cundy, after the Greek capital letter Delta (letter), delta resembling a triangular shape Δ. Deltahedra can be categorized by the property of Convex set, convexity. The simplest convex deltahedron is the regular tetrahedron, a pyramid with four equilateral triangles. There are eight convex deltahedra, which can be used in the applications of chemistry as in the polyhedral skeletal electron pair theory and chemical compounds. There are infinitely many concave deltahedra. Strictly convex deltahedron A polyhedron is said to be ''convex'' if a line between any two of its vertices lies either within its interior or on its boundary, and additionally, if no two faces are Coplanarity, coplanar (lying in the same plane) and no two edges are Collinearity, collinear (segments of the same line), it can be considered as being strictly convex. Of the eight convex set, convex delta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Icosahedron
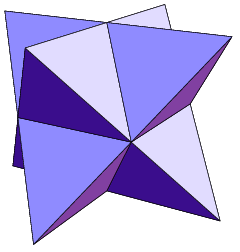
The regular icosahedron (or simply ''icosahedron'') is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with Regular polygon, regular faces to each of its pentagonal faces, or by putting points onto the cube. The resulting polyhedron has 20 equilateral triangles as its faces, 30 edges, and 12 vertices. It is an example of a Platonic solid and of a deltahedron. The icosahedral graph represents the Skeleton (topology), skeleton of a regular icosahedron. Many polyhedra are constructed from the regular icosahedron. A notable example is the stellation of regular icosahedron, which consists of 59 polyhedrons. The great dodecahedron, one of the Kepler–Poinsot polyhedra, is constructed by either stellation or faceting. Some of the Johnson solids can be constructed by removing the pentagonal pyramids. The regular icosahedron's dual polyhedron is the regular dodecahedron, and their relation has a historical background on the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyroelongated Square Bipyramid
In geometry, the gyroelongated square bipyramid is a polyhedron with 16 triangular faces. it can be constructed from a square antiprism by attaching two equilateral square pyramid, equilateral square pyramids to each of its square faces. The same shape is also called hexakaidecadeltahedron, heccaidecadeltahedron, or tetrakis square antiprism; these last names mean a polyhedron with 16 triangular faces. It is an example of deltahedron, and of a Johnson solid. The dual polyhedron of the gyroelongated square bipyramid is a square truncated trapezohedron with eight pentagons and two squares as its faces. The gyroelongated square pyramid appears in chemistry as the basis for the bicapped square antiprismatic molecular geometry, and in mathematical optimization as a solution to the Thomson problem. Construction Like other Gyroelongated bipyramid, gyroelongated bipyramids, the gyroelongated square bipyramid can be constructed by attaching two Equilateral square pyramid, equilateral sq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
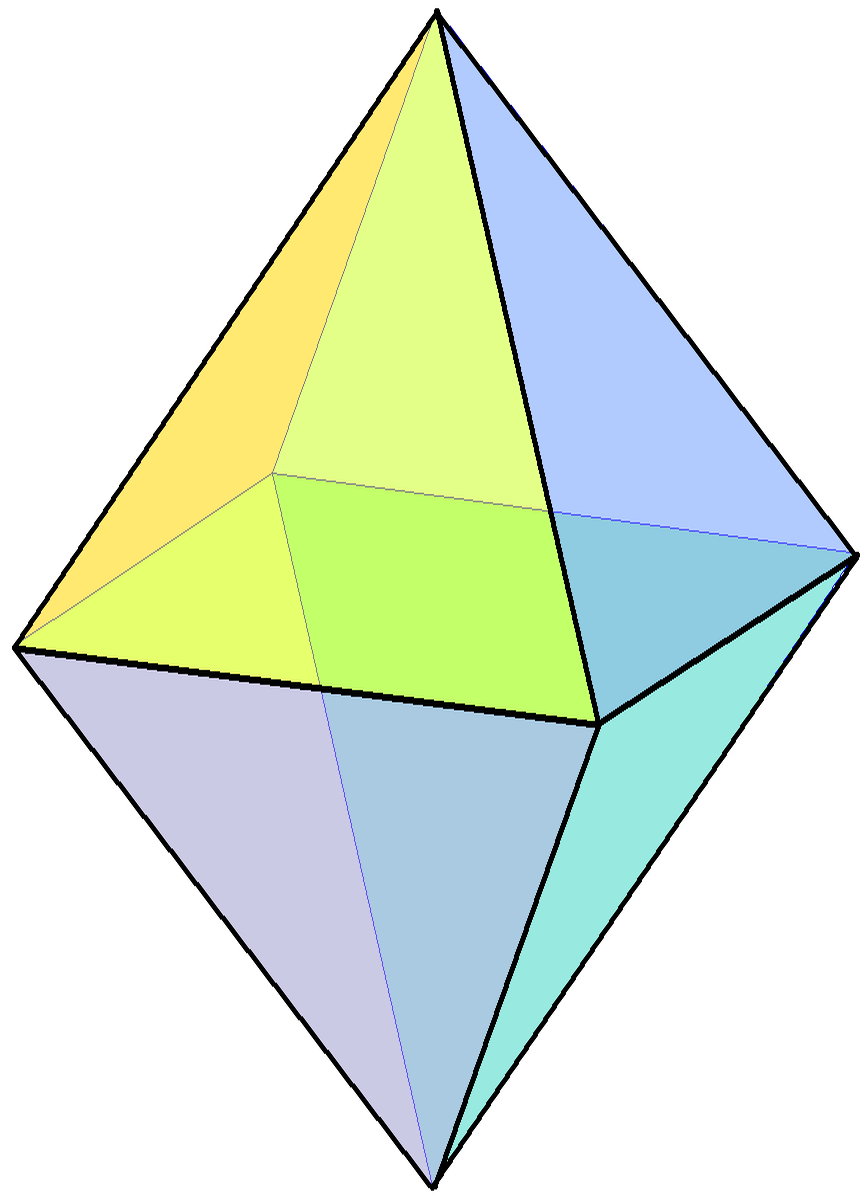
Regular Octahedron
In geometry, a regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. An octahedron, more generally, can be any eight-sided polyhedron; many types of irregular octahedra also exist. A regular octahedron is convex, meaning that for any two points within it, the line segment connecting them lies entirely within it. It is one of the eight convex deltahedra because all of the faces are equilateral triangles. It is a composite polyhedron made by attaching two equilateral square pyramids. Its dual polyhedron is the cube, and they have the same three-dimensional symmetry groups, the octahedral symmetry \mathrm_\mathrm . A regular octahedron is a special case of an octahedron, any eight-sided polyhedron. It is the three-dimensional case of the more general concept of a cross-polytope. As a Platonic solid The regular octahedron is one of the Platonic solids, a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Snub Disphenoid
In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its face (geometry), faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape is also called Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron. The snub disphenoid can be visualized as an atom cluster surrounding a central atom, that is the dodecahedral molecular geometry. Its vertices may be placed in a sphere and can also be used as a minimum possible Lennard-Jones potential among all eight-sphere clusters. The dual polyhedron of the snub disphenoid is the elongated gyrobifastigium. Construction The snub disphenoid can be constructed in different ways. As suggested by the name, the snub disphenoid is constructed from a tetragonal disphenoid by cutting all the edges from its faces, and adding equilateral triangles (the light blue colors in the following image) that are twisted in a certain a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triaugmented Triangular Prism
The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron, composite polyhedron, and Johnson solid. The edges and vertices of the triaugmented triangular prism form a maximal planar graph with 9 vertices and 21 edges, called the Fritsch graph. It was used by Rudolf and Gerda Fritsch to show that Alfred Kempe's attempted proof of the four color theorem was incorrect. The Fritsch graph is one of only six graphs in which every Neighbourhood (graph theory), neighborhood is a 4- or 5-vertex cycle. The dual polyhedron of the triaugmented triangular prism is an associahedron, a p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Bipyramid
A triangular bipyramid is a hexahedron with six triangular faces constructed by attaching two tetrahedra face-to-face. The same shape is also known as a triangular dipyramid or trigonal bipyramid. If these tetrahedra are regular, all faces of a triangular bipyramid are equilateral. It is an example of a deltahedron, composite polyhedron, and Johnson solid. Many polyhedra are related to the triangular bipyramid, such as similar shapes derived from different approaches and the triangular prism as its dual polyhedron. Applications of a triangular bipyramid include trigonal bipyramidal molecular geometry which describes its atom cluster, a solution of the Thomson problem, and the representation of color order systems by the eighteenth century. Special cases As a right bipyramid Like other bipyramids, a triangular bipyramid can be constructed by attaching two tetrahedra face-to-face. These tetrahedra cover their triangular base, and the resulting polyhedron has six triangles, fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Bipyramid
The pentagonal bipyramid (or pentagonal dipyramid) is a polyhedron with ten triangular faces. It is constructed by attaching two pentagonal pyramids to each of their bases. If the triangular faces are equilateral, the pentagonal bipyramid is an example of deltahedra, composite polyhedron, and Johnson solid. The pentagonal bipyramid may be represented as four-connected well-covered graph. This polyhedron may be used in the chemical compound as the description of an atom cluster known as pentagonal bipyramidal molecular geometry, as a solution in Thomson problem, as well as in decahedral nanoparticles. Special cases As a right bipyramid Like other bipyramids, the pentagonal bipyramid can be constructed by attaching the base of two pentagonal pyramids. These pyramids cover their pentagonal base, such that the resulting polyhedron has ten triangles as its faces, fifteen edges, and seven vertices. The pentagonal bipyramid is said to be right if the pyramids are symmetri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tetrahedron is the simplest of all the ordinary convex polytope, convex polyhedra. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean geometry, Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid (geometry), pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron, the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such net (polyhedron), nets. For any tetrahedron there exists a sphere (called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedral Skeletal Electron Pair Theory
In chemistry the polyhedral skeletal electron pair theory (PSEPT) provides electron counting rules useful for predicting the structures of clusters such as borane and carborane clusters. The electron counting rules were originally formulated by Kenneth Wade, and were further developed by others including Michael Mingos; they are sometimes known as Wade's rules or the Wade–Mingos rules. The rules are based on a molecular orbital treatment of the bonding. These notes contained original material that served as the basis of the sections on the 4''n'', 5''n'', and 6''n'' rules. These rules have been extended and unified in the form of the Jemmis ''mno'' rules. Predicting structures of cluster compounds Different rules (4''n'', 5''n'', or 6''n'') are invoked depending on the number of electrons per vertex. The 4''n'' rules are reasonably accurate in predicting the structures of clusters having about 4 electrons per vertex, as is the case for many boranes and carboranes. For su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surface (mathematics), surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term ''polyhedron'' is often used to refer implicitly to the whole structure (mathematics), structure formed by a solid polyhedron, its polyhedral surface, its faces, its edges, and its vertices. There are many definitions of polyhedron. Nevertheless, the polyhedron is typically understood as a generalization of a two-dimensional polygon and a three-dimensional specialization of a polytope, a more general concept in any number of dimensions. Polyhedra have several general characteristics that include the number of faces, topological classification by Eule ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Compounds
A chemical compound is a chemical substance composed of many identical molecules (or molecular entities) containing atoms from more than one chemical element held together by chemical bonds. A molecule consisting of atoms of only one element is therefore not a compound. A compound can be transformed into a different substance by a chemical reaction, which may involve interactions with other substances. In this process, bonds between atoms may be broken or new bonds formed or both. There are four major types of compounds, distinguished by how the constituent atoms are bonded together. Molecular compounds are held together by covalent bonds; ionic compounds are held together by ionic bonds; intermetallic compounds are held together by metallic bonds; coordination complexes are held together by coordinate covalent bonds. Non-stoichiometric compounds form a disputed marginal case. A chemical formula specifies the number of atoms of each element in a compound molecule, us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedral Molecular Geometry
In a tetrahedral molecular geometry, a central atom is located at the center with four substituents that are located at the corners of a tetrahedron. The bond angles are arccos(−) = 109.4712206...° ≈ 109.5° when all four substituents are the same, as in methane () as well as its heavier analogues. Methane and other perfectly symmetrical tetrahedral molecules belong to point group ''Td'', but most tetrahedral molecules have lower symmetry. Tetrahedral molecules can be chiral. Tetrahedral bond angle The bond angle for a symmetric tetrahedral molecule such as CH4 may be calculated using the dot product of two vectors. As shown in the diagram at left, the molecule can be inscribed in a cube with the tetravalent atom (e.g. carbon) at the cube centre which is the origin of coordinates, O. The four monovalent atoms (e.g. hydrogens) are at four corners of the cube (A, B, C, D) chosen so that no two atoms are at adjacent corners linked by only one cube edge. If the edge len ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |