|
Corner Solution
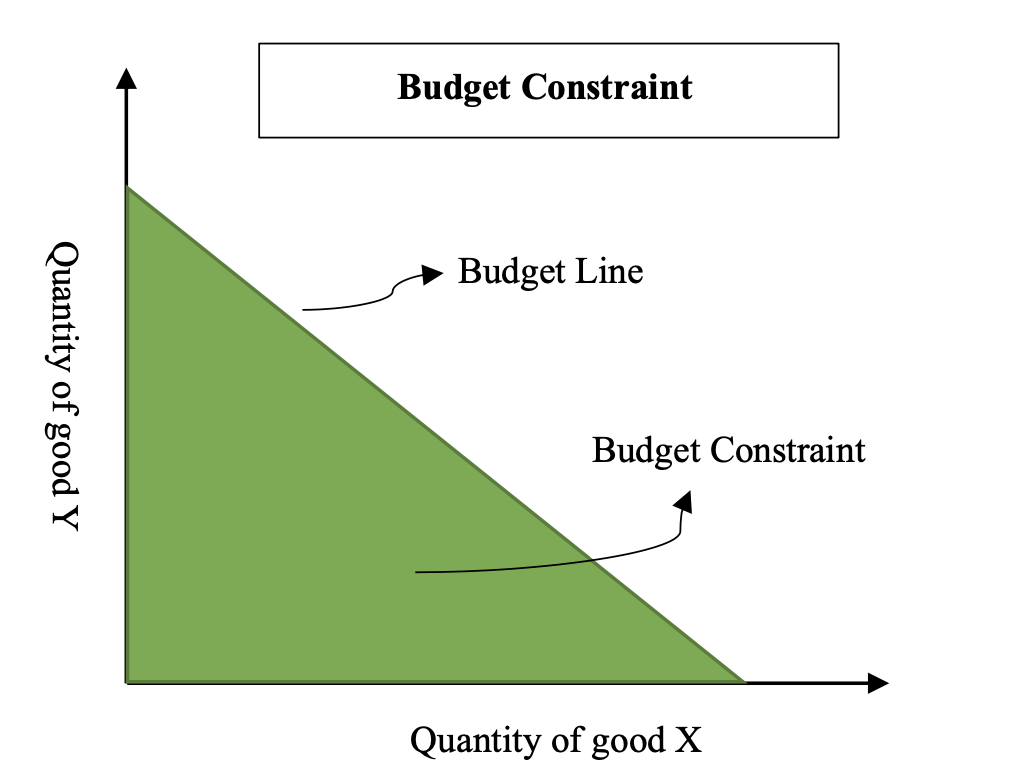
In mathematics and economics, a corner solution is a special solution to an agent's maximization problem in which the quantity of one of the arguments in the maximized function is zero. In non-technical terms, a corner solution is when the chooser is either unwilling or unable to make a trade-off between goods. In economics In the context of economics the corner solution is best characterised by when the highest indifference curve attainable is not tangential to the budget line, in this scenario the consumer puts their entire budget into purchasing as much of one of the goods as possible and none of any other. When the slope of the indifference curve is greater than the slope of the budget line, the consumer is willing to give up more of good 1 for a unit of good 2 than is required by the market. Thus, it follows that if the slope of the indifference curve is strictly greater than the slope of the budget line: \text > \text; \ \forall \text Then the result will be a corner so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Objective Function
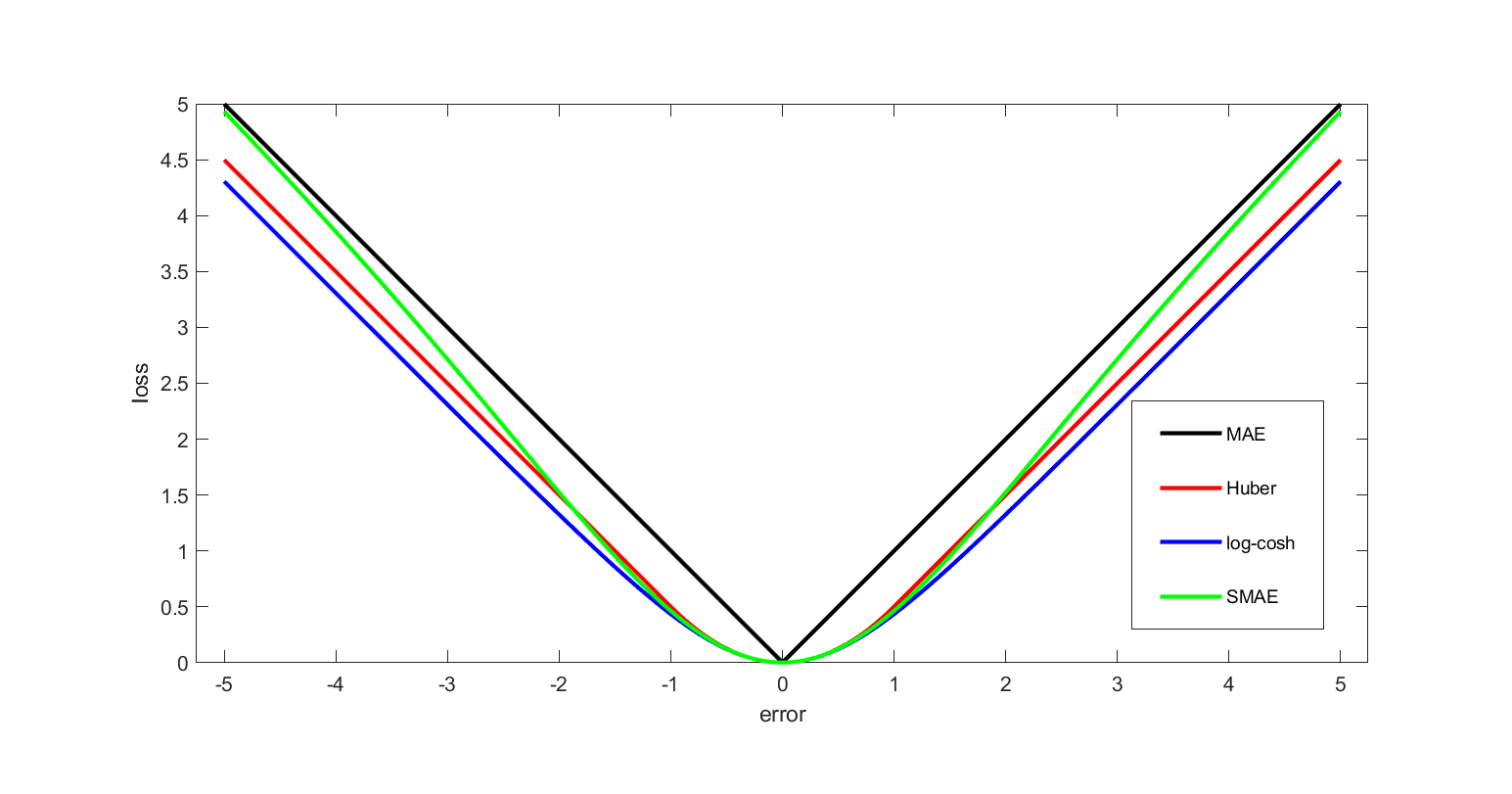
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economics, for example, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Utility
In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings. * In a normative context, utility refers to a goal or objective that we wish to maximize, i.e., an objective function. This kind of utility bears a closer resemblance to the original utilitarian concept, developed by moral philosophers such as Jeremy Bentham and John Stuart Mill. * In a descriptive context, the term refers to an ''apparent'' objective function; such a function is revealed by a person's behavior, and specifically by their preferences over lotteries, which can be any quantified choice. The relationship between these two kinds of utility functions has been a source of controversy among both economists and ethicists, with most maintaining that the two are distinct but generally related. Utility function Consider a set of alternatives among which a person has a preference ordering. A utility fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Assumptions Section
Assumption, in Christianity, refers to the Assumption of Mary, a belief in the taking up of the Virgin Mary into heaven. Assumption may also refer to: Places * Assumption, Alberta, Canada * Assumption, Illinois, United States ** Assumption Township, Christian County, Illinois * Assumption Island, Seychelles ** Assumption Island Airport * Assumption, Minnesota, United States * Assumption, Nebraska, United States * Assumption, Ohio, United States * Assumption Parish, Louisiana, United States Arts, entertainment, and media * "Assumption" (short story), a 1929 story by Samuel Beckett * Assumption of Moses, a Jewish apocryphal pseudepigraphical work of uncertain date and authorship * "Assumptions" (''Doctors''), a 2003 television episode * Assumption (film), a 2017 short film by Anthony Leone * "Assumptions" (''Law & Order: Special Victims Unit''), a 2019 television episode * "Assumptions" (song), 2021 song by Sam Gellaitry Churches * Assumption Chapel, Minnesota, United ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrangian
Lagrangian may refer to: Mathematics * Lagrangian function, used to solve constrained minimization problems in optimization theory; see Lagrange multiplier ** Lagrangian relaxation, the method of approximating a difficult constrained problem with an easier problem having an enlarged feasible set ** Lagrangian dual problem, the problem of maximizing the value of the Lagrangian function, in terms of the Lagrange-multiplier variable; See Dual problem * Lagrangian, a functional whose extrema are to be determined in the calculus of variations * Lagrangian submanifold, a class of submanifolds in symplectic geometry * Lagrangian system, a pair consisting of a smooth fiber bundle and a Lagrangian density Physics * Lagrangian mechanics, a formulation of classical mechanics * Lagrangian (field theory), a formalism in classical field theory * Lagrangian point, a position in an orbital configuration of two large bodies * Lagrangian coordinates, a way of describing the motions of particles of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Utility Function
In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings. * In a Normative economics, normative context, utility refers to a goal or objective that we wish to maximize, i.e., an objective function. This kind of utility bears a closer resemblance to the original Utilitarianism, utilitarian concept, developed by moral philosophers such as Jeremy Bentham and John Stuart Mill. * In a Positive economics, descriptive context, the term refers to an ''apparent'' objective function; such a function is Revealed preference, revealed by a person's behavior, and specifically by their preferences over Lottery (decision theory), lotteries, which can be any quantified choice. The relationship between these two kinds of utility functions has been a source of controversy among both Economics, economists and Ethics, ethicists, with most maintaining that the two are distinct but generally re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Consumer Theory
The theory of consumer choice is the branch of microeconomics that relates preferences to consumption expenditures and to consumer demand curves. It analyzes how consumers maximize the desirability of their consumption (as measured by their preferences subject to limitations on their expenditures), by maximizing utility subject to a consumer budget constraint. Factors influencing consumers' evaluation of the utility of goods include: income level, cultural factors, product information and physio-psychological factors. Consumption is separated from production, logically, because two different economic agents are involved. In the first case, consumption is determined by the individual. Their specific tastes or preferences determine the amount of utility they derive from goods and services they consume. In the second case, a producer has different motives to the consumer in that they are focussed on the profit they make. This is explained further by producer theory. The models ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Extrema
In mathematical analysis, the maximum and minimum of a function are, respectively, the greatest and least value taken by the function. Known generically as extremum, they may be defined either within a given range (the ''local'' or ''relative'' extrema) or on the entire domain (the ''global'' or ''absolute'' extrema) of a function. Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. In statistics, the corresponding concept is the sample maximum and minimum. Definition A real-valued function ''f'' defined on a domain ''X'' has a global (or absolute) maximum point at ''x''∗, if for all ''x'' in ''X''. Similarly, the function has a global (or absolute) minimum point at ''x''∗, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Elegance
Mathematics is a field of study that discovers and organizes methods, theories and theorems that are developed and proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of abstract objects that consist of either abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to prove properties of objects, a ''proof'' consisting of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstracti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |