|
Convolution Random Number Generator
In statistics and computer software, a convolution random number generator is a pseudo-random number sampling method that can be used to generate random variates from certain classes of probability distribution. The particular advantage of this type of approach is that it allows advantage to be taken of existing software for generating random variates from other, usually non-uniform, distributions. However, faster algorithms may be obtainable for the same distributions by other more complicated approaches.Antonov, N. (2020)''Random number generator based on multiplicative convolution transform.''/ref> A number of distributions can be expressed in terms of the (possibly weighted) sum of two or more random variables from other distributions. (The distribution of the sum is the convolution of the distributions of the individual random variables). Example Consider the problem of generating a random variable with an Erlang distribution The Erlang distribution is a two-paramete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Software
Software consists of computer programs that instruct the Execution (computing), execution of a computer. Software also includes design documents and specifications. The history of software is closely tied to the development of digital computers in the mid-20th century. Early programs were written in the machine language specific to the hardware. The introduction of high-level programming languages in 1958 allowed for more human-readable instructions, making software development easier and more portable across different computer architectures. Software in a programming language is run through a compiler or Interpreter (computing), interpreter to execution (computing), execute on the architecture's hardware. Over time, software has become complex, owing to developments in Computer network, networking, operating systems, and databases. Software can generally be categorized into two main types: # operating systems, which manage hardware resources and provide services for applicat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudo-random Number Sampling
Non-uniform random variate generation or pseudo-random number sampling is the numerical practice of generating pseudo-random numbers (PRN) that follow a given probability distribution. Methods are typically based on the availability of a uniformly distributed PRN generator. Computational algorithms are then used to manipulate a single random variate, ''X'', or often several such variates, into a new random variate ''Y'' such that these values have the required distribution. The first methods were developed for Monte-Carlo simulations in the Manhattan project, published by John von Neumann in the early 1950s. Finite discrete distributions For a discrete probability distribution with a finite number ''n'' of indices at which the probability mass function ''f'' takes non-zero values, the basic sampling algorithm is straightforward. The interval [0, 1) is divided in ''n'' intervals [0, ''f''(1)), [''f''(1), ''f''(1) + ''f''(2)), ... The width of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variate
In probability and statistics, a random variate or simply variate is a particular outcome or ''realization'' of a random variable; the random variates which are other outcomes of the same random variable might have different values ( random numbers). A random deviate or simply deviate is the difference of a random variate with respect to the distribution central location (e.g., mean), often divided by the standard deviation of the distribution (i.e., as a standard score). Random variates are used when simulating processes driven by random influences (stochastic processes). In modern applications, such simulations would derive random variates corresponding to any given probability distribution from computer procedures designed to create random variates corresponding to a uniform distribution, where these procedures would actually provide values chosen from a uniform distribution of pseudorandom numbers. Procedures to generate random variates corresponding to a given distribut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathematical definition refers to neither randomness nor variability but instead is a mathematical function (mathematics), function in which * the Domain of a function, domain is the set of possible Outcome (probability), outcomes in a sample space (e.g. the set \ which are the possible upper sides of a flipped coin heads H or tails T as the result from tossing a coin); and * the Range of a function, range is a measurable space (e.g. corresponding to the domain above, the range might be the set \ if say heads H mapped to -1 and T mapped to 1). Typically, the range of a random variable is a subset of the Real number, real numbers. Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice, d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The term ''convolution'' refers to both the resulting function and to the process of computing it. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result (see #Properties, commutativity). Graphically, it expresses how the 'shape' of one function is modified by the other. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution f*g differs from cross-correlation f \star g only in that either f(x) or g(x) is reflected about the y-axis in convolution; thus i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erlang Distribution
The Erlang distribution is a two-parameter family of continuous probability distributions with Support (mathematics), support x \in [0, \infty). The two parameters are: * a positive integer k, the "shape", and * a positive real number \lambda, the "rate". The "scale", \beta, the reciprocal of the rate, is sometimes used instead. The Erlang distribution is the distribution of a sum of k Independence (probability theory), independent exponential distribution, exponential variables with mean 1/\lambda each. Equivalently, it is the distribution of the time until the ''k''th event of a Poisson process with a rate of \lambda. The Erlang and Poisson distributions are complementary, in that while the Poisson distribution counts the events that occur in a fixed amount of time, the Erlang distribution counts the amount of time until the occurrence of a fixed number of events. When k=1, the distribution simplifies to the exponential distribution. The Erlang distribution is a special ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Distribution
In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the distance between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate; the distance parameter could be any meaningful mono-dimensional measure of the process, such as time between production errors, or length along a roll of fabric in the weaving manufacturing process. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts. The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
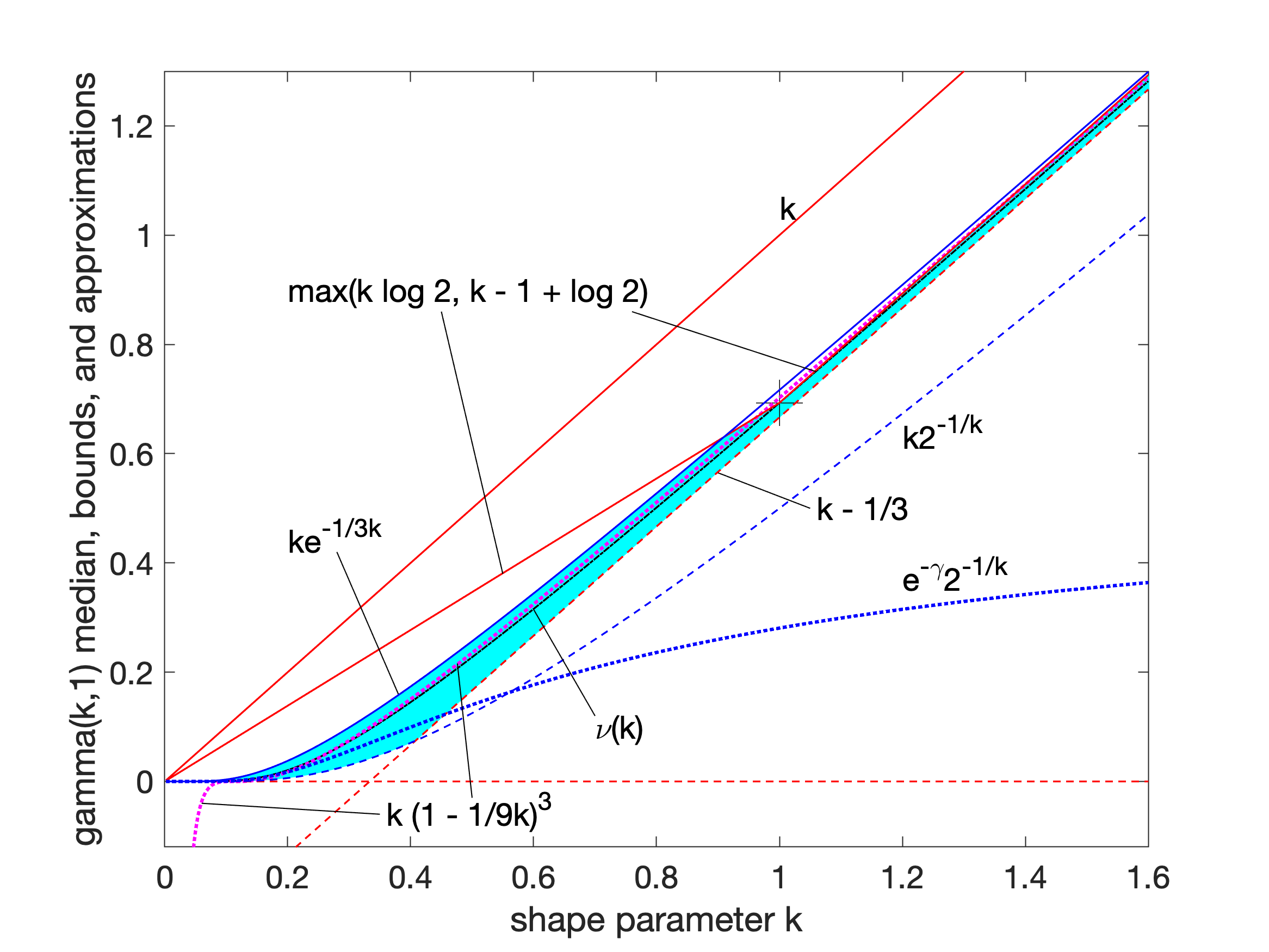
Gamma Distribution
In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: # With a shape parameter and a scale parameter # With a shape parameter \alpha and a rate parameter In each of these forms, both parameters are positive real numbers. The distribution has important applications in various fields, including econometrics, Bayesian statistics, and life testing. In econometrics, the (''α'', ''θ'') parameterization is common for modeling waiting times, such as the time until death, where it often takes the form of an Erlang distribution for integer ''α'' values. Bayesian statisticians prefer the (''α'',''λ'') parameterization, utilizing the gamma distribution as a conjugate prior for several inverse scale parameters, facilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shape Parameter
In probability theory and statistics, a shape parameter (also known as form parameter) is a kind of numerical parameter of a parametric family of probability distributionsEveritt B.S. (2002) Cambridge Dictionary of Statistics. 2nd Edition. CUP. that is neither a location parameter nor a scale parameter (nor a function of these, such as a rate parameter). Such a parameter must affect the ''shape (geometry), shape'' of a distribution rather than simply shifting it (as a location parameter does) or stretching/shrinking it (as a scale parameter does). For example, "peakedness" refers to how round the main peak is. Estimation Many estimators measure location or scale; however, estimators for shape parameters also exist. Most simply, they can be estimated in terms of the higher moment (mathematics), moments, using the Method of moments (statistics), method of moments, as in the ''skewness'' (3rd moment) or ''kurtosis'' (4th moment), if the higher moments are defined and finite. Estimato ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |