|
Constant Elasticity Of Substitution
Constant elasticity of substitution (CES) is a common specification of many production functions and utility function In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings. * In a Normative economics, normative context, utility refers to a goal or ob ...s in neoclassical economics. CES holds that the ability to substitute one input factor with another (for example labour with capital) to maintain the same level of production stays constant over different production levels. For utility functions, CES means the consumer has constant preferences of how they would like to substitute different goods (for example labour with consumption) while keeping the same level of utility, for all levels of utility. What this means is that both producers and consumers have similar input structures and preferences no matter the level of output or utility. The vital economic element o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Production Function
In economics, a production function gives the technological relation between quantities of physical inputs and quantities of output of goods. The production function is one of the key concepts of mainstream economics, mainstream neoclassical economics, neoclassical theories, used to define marginal product and to distinguish allocative efficiency, a key focus of economics. One important purpose of the production function is to address allocative efficiency in the use of factor inputs in production and the resulting distribution of income to those factors, while abstracting away from the technological problems of achieving technical efficiency, as an engineer or professional manager might understand it. For modelling the case of many outputs and many inputs, researchers often use the so-called Shephard's distance functions or, alternatively, directional distance functions, which are generalizations of the simple production function in economics. In macroeconomics, aggregate produc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
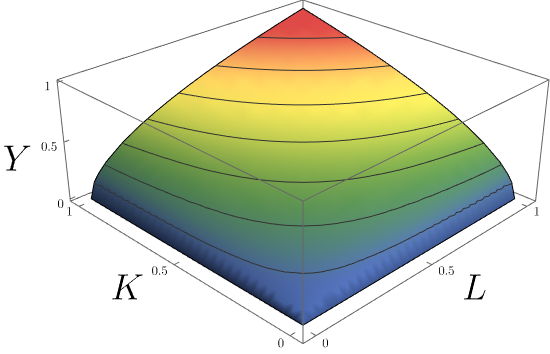
Cobb–Douglas Production Function
In economics and econometrics, the Cobb–Douglas production function is a particular functional form of the production function, widely used to represent the technological relationship between the amounts of two or more inputs (particularly physical capital and labor) and the amount of output that can be produced by those inputs. The Cobb–Douglas form was developed and tested against statistical evidence by Charles Cobb and Paul Douglas between 1927 and 1947; according to Douglas, the functional form itself was developed earlier by Philip Wicksteed. Formulation In its most standard form for production of a single good with two factors, the function is given by: : Y(L,K)=AL^\beta K^\alpha where: * ''Y'' = total production (the real value of all goods produced in a year or 365.25 days) * ''L'' = labour input (person-hours worked in a year or 365.25 days) * ''K'' = capital input (a measure of all machinery, equipment, and buildings; the value of capital input divided by t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Avinash Dixit
Avinash Kamalakar Dixit (born 6 August 1944) is an Indian-American economist. He is the John J. F. Sherrerd '52 University Professor of Economics Emeritus at Princeton University, and has been distinguished adjunct professor of economics at Lingnan University (Hong Kong), senior research fellow at Nuffield College, Oxford and Sanjaya Lall Senior Visiting Research Fellow at Green Templeton College, Oxford. Education Dixit received a B.Sc. from University of Mumbai ( St. Xavier's College) in 1963 in Mathematics and Physics, a B.A. from Cambridge University in 1965 in Mathematics ( Corpus Christi College, First Class), and a Ph.D. in 1968 from the Massachusetts Institute of Technology in Economics. Career Dixit is the John J. F. Sherrerd '52 University Professor of Economics at Princeton University since July 1989, and Emeritus since 2010. He was also distinguished adjunct professor of economics at Lingnan University (Hong Kong), senior research fellow at Nuffield ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Demand Function
In economics, an inverse demand function is the mathematical relationship that expresses price as a function of quantity demanded (it is therefore also known as a price function). Historically, the economists first expressed the price of a good as a function of demand (holding the other economic variables, like income, constant), and plotted the price-demand relationship with demand on the x (horizontal) axis (the demand curve). Later the additional variables, like prices of other goods, came into analysis, and it became more convenient to express the demand as a multivariate function (the demand function): = f(, , ...), so the original demand curve now depicts the ''inverse'' demand function = f^() with extra variables fixed. Definition In mathematical terms, if the demand function is = f(), then the inverse demand function is = f^(). The value of the inverse demand function is the highest price that could be charged and still generate the quantity demanded. This is useful ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indirect Utility Function
__NOTOC__ In economics, a consumer's indirect utility function v(p, w) gives the consumer's maximal attainable utility when faced with a vector p of goods prices and an amount of income w. It reflects both the consumer's preferences and market conditions. This function is called indirect because consumers usually think about their preferences in terms of what they consume rather than prices. A consumer's indirect utility v(p, w) can be computed from their utility function u(x), defined over vectors x of quantities of consumable goods, by first computing the most preferred affordable bundle, represented by the vector x(p, w) by solving the utility maximization problem, and second, computing the utility u(x(p, w)) the consumer derives from that bundle. The resulting indirect utility function is :v(p,w)=u(x(p,w)). The indirect utility function is: *Continuous on R''n''+ × R+ where ''n'' is the number of goods; *Decreasing in prices; *Strictly increasing in income; * Homogenous wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expenditure Function
In microeconomics, the expenditure function represents the minimum amount of expenditure needed to achieve a given level of utility, given a utility function and the prices of goods. Formally, if there is a utility function u that describes preferences over ''n ''goods, the expenditure function e(p, u^*) is defined as: :e(p, u^*) = \min_ p \cdot x where p is the price vector u^* is the desired utility level, \geq(u^*) = \ is the set of providing at least utility u^*. Expressed equivalently, the individual minimizes expenditure x_1p_1+\dots +x_n p_n subject to the minimal utility constraint that u(x_1, \dots , x_n) \ge u^*, giving optimal quantities to consume of the various goods as x_1^*, \dots x_n^* as function of u^* and the prices; then the expenditure function is :e(p_1, \dots , p_n ; u^*)=p_1 x_1^*+\dots + p_n x_n^*. Properties Suppose u is a continuous utility function representing a locally non-satiated preference relation on \textbf R^n_+. Then e(p, u^*) is # Homo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homothetic Preferences
In consumer theory, a consumer's preferences are called homothetic if they can be represented by a utility function which is homogeneous of degree 1. For example, in an economy with two goods x,y, homothetic preferences can be represented by a utility function u that has the following property: for every a>0: ::u(a\cdot x,a\cdot y) = a\cdot u(x,y) In mathematics, a homothetic function is a monotonic transformation of a function which is homogeneous; however, since ordinal utility functions are only defined up to an increasing monotonic transformation, there is a small distinction between the two concepts in consumer theory. In a model where competitive consumers optimize homothetic utility functions subject to a budget constraint, the ratios of goods demanded by consumers will depend only on relative prices, not on income or scale. This translates to a linear expansion path in income: the slope of indifference curves is constant along rays beginning at the origin. This is t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paul Armington
Paul may refer to: People * Paul (given name) Paul is a common Latin Language, Latin masculine given name in countries and ethnicities with a Christian heritage (Eastern Orthodox Church, Eastern Orthodoxy, Catholic Church, Catholicism, Protestantism) and, beyond Europe, in Christian religiou ..., a given name, including a list of people * Paul (surname), a list of people * Paul the Apostle, an apostle who wrote many of the books of the New Testament * Ray Hildebrand, half of the singing duo Paul & Paula * Paul Stookey, one-third of the folk music trio Peter, Paul and Mary * Billy Paul, stage name of American soul singer Paul Williams (1934–2016) * Vinnie Paul, drummer for American Metal band Pantera * Paul Avril, pseudonym of Édouard-Henri Avril (1849–1928), French painter and commercial artist * Paul, pen name under which Walter Scott wrote ''Paul's letters to his Kinsfolk'' in 1816 * Jean Paul, pen name of Johann Paul Friedrich Richter (1763–1825), German Romantic write ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
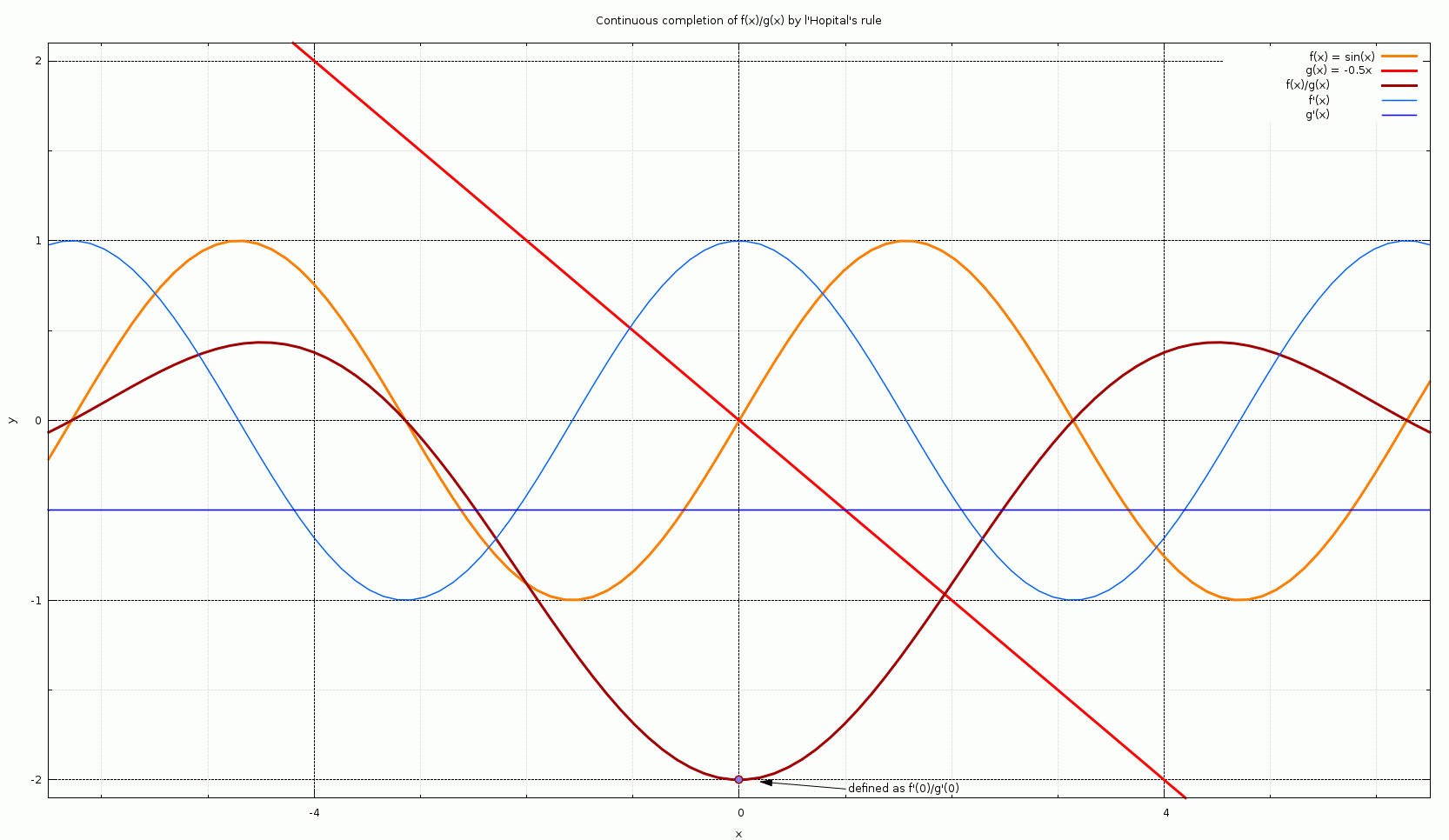
L'Hôpital's Rule
L'Hôpital's rule (, ), also known as Bernoulli's rule, is a mathematical theorem that allows evaluating limits of indeterminate forms using derivatives. Application (or repeated application) of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. The rule is named after the 17th-century French mathematician Guillaume de l'Hôpital. Although the rule is often attributed to de l'Hôpital, the theorem was first introduced to him in 1694 by the Swiss mathematician Johann Bernoulli. L'Hôpital's rule states that for functions and which are defined on an open interval and differentiable on I\setminus \ for a (possibly infinite) accumulation point of , if \lim \limits_f(x)=\lim \limits_g(x)=0 \text\pm\infty, and g'(x)\ne 0 for all in I\setminus \, and \lim \limits_\frac exists, then :\lim_\frac = \lim_\frac. The differentiation of the numerator and denominator often simplifies the quotient or converts it to a limit t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Substitute Good
In microeconomics, substitute goods are two goods that can be used for the same purpose by consumers. That is, a consumer perceives both goods as similar or comparable, so that having more of one good causes the consumer to desire less of the other good. Contrary to complementary goods and independent goods, substitute goods may replace each other in use due to changing economic conditions. An example of substitute goods is Coca-Cola and Pepsi; the interchangeable aspect of these goods is due to the similarity of the purpose they serve, i.e. fulfilling customers' desire for a soft drink. These types of substitutes can be referred to as close substitutes. Substitute goods are commodity which the consumer demanded to be used in place of another good. Economic theory describes two goods as being close substitutes if three conditions hold: # products have the same or similar performance characteristics # products have the same or similar occasion for use and # products are sold in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Consumer Theory
The theory of consumer choice is the branch of microeconomics that relates preferences to consumption expenditures and to consumer demand curves. It analyzes how consumers maximize the desirability of their consumption (as measured by their preferences subject to limitations on their expenditures), by maximizing utility subject to a consumer budget constraint. Factors influencing consumers' evaluation of the utility of goods include: income level, cultural factors, product information and physio-psychological factors. Consumption is separated from production, logically, because two different economic agents are involved. In the first case, consumption is determined by the individual. Their specific tastes or preferences determine the amount of utility they derive from goods and services they consume. In the second case, a producer has different motives to the consumer in that they are focussed on the profit they make. This is explained further by producer theory. The models ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Equilibrium
In economics, general equilibrium theory attempts to explain the behavior of supply, demand, and prices in a whole economy with several or many interacting markets, by seeking to prove that the interaction of demand and supply will result in an overall general equilibrium. General equilibrium theory contrasts with the theory of ''partial'' equilibrium, which analyzes a specific part of an economy while its other factors are held constant. General equilibrium theory both studies economies using the model of equilibrium pricing and seeks to determine in which circumstances the assumptions of general equilibrium will hold. The theory dates to the 1870s, particularly the work of French economist Léon Walras in his pioneering 1874 work ''Elements of Pure Economics''. The theory reached its modern form with the work of Lionel W. McKenzie (Walrasian theory), Kenneth Arrow and Gérard Debreu (Hicksian theory) in the 1950s. Overview Broadly speaking, general equilibrium tries to give a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |