|
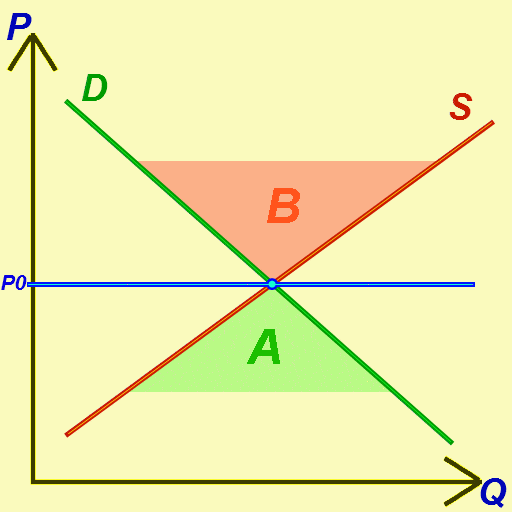
Comparative Statics
In economics, comparative statics is the comparison of two different economic outcomes, before and after a change in some underlying exogenous variable, exogenous parameter. As a type of ''static analysis'' it compares two different economic equilibrium, equilibrium states, after the process of adjustment (if any). It does not study the motion towards equilibrium, nor the process of the change itself. Comparative statics is commonly used to study changes in supply and demand when analyzing a single Market (economics), market, and to study changes in monetary policy, monetary or fiscal policy when analyzing the whole macroeconomics, economy. Comparative statics is a tool of analysis in microeconomics (including general equilibrium analysis) and macroeconomics. Comparative statics was formalized by Sir John Richard Hicks, John R. Hicks (1939) and Paul A. Samuelson (1947) (Kehoe, 1987, p. 517) but was presented graphically from at least the 1870s. For models of stable equili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supply-and-demand
In microeconomics, supply and demand is an economic model of price determination in a Market (economics), market. It postulates that, Ceteris_paribus#Applications, holding all else equal, the unit price for a particular Good (economics), good or other traded item in a perfect competition, perfectly competitive market, will vary until it settles at the market clearing, market-clearing price, where the quantity demanded equals the quantity supplied such that an economic equilibrium is achieved for price and quantity transacted. The concept of supply and demand forms the theoretical basis of modern economics. In situations where a firm has market power, its decision on how much output to bring to market influences the market price, in violation of perfect competition. There, a more complicated model should be used; for example, an oligopoly or product differentiation, differentiated-product model. Likewise, where a buyer has market power, models such as monopsony will be more a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comparative Dynamics
In economics, economic equilibrium is a situation in which the economic forces of supply and demand are balanced, meaning that economic variables will no longer change. Market equilibrium in this case is a condition where a market price is established through competition such that the amount of goods or services sought by buyers is equal to the amount of goods or services produced by sellers. This price is often called the competitive price or market clearing price and will tend not to change unless demand or supply changes, and quantity is called the "competitive quantity" or market clearing quantity. Understanding economic equilibrium An economic equilibrium is a situation when the economic agent cannot change the situation by adopting any strategy. The concept has been borrowed from the physical sciences. Take a system where physical forces are balanced for instance.This economically interpreted means no further change ensues. Properties of equilibrium Three basic propertie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stability Theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions. The heat equation, for example, is a stable partial differential equation because small perturbations of initial data lead to small variations in temperature at a later time as a result of the maximum principle. In partial differential equations one may measure the distances between functions using Lp space, Lp norms or the sup norm, while in differential geometry one may measure the distance between spaces using the Gromov–Hausdorff convergence, Gromov–Hausdorff distance. In dynamical systems, an orbit (dynamics), orbit is called ''Lyapunov stability, Lyapunov stable'' if the forward orbit of any point is in a small enough neighborhood or it stays in a small (but perhaps, larger) neighborhood. Various criteria have been developed to prove stability or instability of an orbit. Under favorable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Derivative
A time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function. The variable denoting time is usually written as t. Notation A variety of notations are used to denote the time derivative. In addition to the normal ( Leibniz's) notation, :\frac A very common short-hand notation used, especially in physics, is the 'over-dot'. I.E. :\dot (This is called Newton's notation) Higher time derivatives are also used: the second derivative with respect to time is written as :\frac with the corresponding shorthand of \ddot. As a generalization, the time derivative of a vector, say: : \mathbf v = \left v_1,\ v_2,\ v_3, \ldots \right is defined as the vector whose components are the derivatives of the components of the original vector. That is, : \frac = \left \frac,\frac ,\frac , \ldots \right . Use in physics Time derivatives are a key concept in physics. For example, for a changing position x, its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Demand Curve
A demand curve is a graph depicting the inverse demand function, a relationship between the price of a certain commodity (the ''y''-axis) and the quantity of that commodity that is demanded at that price (the ''x''-axis). Demand curves can be used either for the price-quantity relationship for an individual consumer (an individual demand curve), or for all consumers in a particular market (a market demand curve). It is generally assumed that demand curves slope down, as shown in the adjacent image. This is because of the law of demand: for most goods, the quantity demanded falls if the price rises. Certain unusual situations do not follow this law. These include Veblen goods, Giffen goods, and speculative bubbles where buyers are attracted to a commodity if its price rises. Demand curves are used to estimate behaviour in competitive markets and are often combined with supply curves to find the equilibrium price (the price at which sellers together are willing to sell the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the matrix and the linear map represented, on a given basis (linear algebra), basis, by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible matrix, invertible and the corresponding linear map is an linear isomorphism, isomorphism. However, if the determinant is zero, the matrix is referred to as singular, meaning it does not have an inverse. The determinant is completely determined by the two following properties: the determinant of a product of matrices is the product of their determinants, and the determinant of a triangular matrix is the product of its diagonal entries. The determinant of a matrix is :\begin a & b\\c & d \end=ad-bc, and the determinant of a matrix is : \begin a & b & c \\ d & e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Econometrica
''Econometrica'' is a peer-reviewed academic journal of economics, publishing articles in many areas of economics, especially econometrics. It is published by Wiley-Blackwell on behalf of the Econometric Society. The current editor-in-chief is Guido Imbens. History ''Econometrica'' was established in 1933. Its first editor was Ragnar Frisch, recipient of the first Nobel Memorial Prize in Economic Sciences in 1969, who served as an editor from 1933 to 1954. Although ''Econometrica'' is currently published entirely in English, the first few issues also contained scientific articles written in French. Indexing and abstracting ''Econometrica'' is abstracted and indexed in: * Scopus * EconLit * Social Sciences Citation Index According to the ''Journal Citation Reports'', the journal has a 2020 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Differentiation
In mathematics, the total derivative of a function at a point is the best linear approximation near this point of the function with respect to its arguments. Unlike partial derivatives, the total derivative approximates the function with respect to all of its arguments, not just a single one. In many situations, this is the same as considering all partial derivatives simultaneously. The term "total derivative" is primarily used when is a function of several variables, because when is a function of a single variable, the total derivative is the same as the ordinary derivative of the function. The total derivative as a linear map Let U \subseteq \R^n be an open subset. Then a function f:U \to \R^m is said to be (totally) differentiable at a point a\in U if there exists a linear transformation df_a:\R^n \to \R^m such that :\lim_ \frac=0. The linear map df_a is called the (total) derivative or (total) differential of f at a. Other notations for the total derivative inclu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cramer's Rule
In linear algebra, Cramer's rule is an explicit formula for the solution of a system of linear equations with as many equations as unknowns, valid whenever the system has a unique solution. It expresses the solution in terms of the determinants of the (square) coefficient matrix and of matrices obtained from it by replacing one column by the column vector of right-sides of the equations. It is named after Gabriel Cramer, who published the rule for an arbitrary number of unknowns in 1750, although Colin Maclaurin also published special cases of the rule in 1748, and possibly knew of it as early as 1729. Cramer's rule, implemented in a naive way, is computationally inefficient for systems of more than two or three equations. In the case of equations in unknowns, it requires computation of determinants, while Gaussian elimination produces the result with the same (up to a constant factor independent of ) computational complexity as the computation of a single determinant. Moreo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobian Matrix
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. If this matrix is square, that is, if the number of variables equals the number of components of function values, then its determinant is called the Jacobian determinant. Both the matrix and (if applicable) the determinant are often referred to simply as the Jacobian. They are named after Carl Gustav Jacob Jacobi. The Jacobian matrix is the natural generalization to vector valued functions of several variables of the derivative and the differential of a usual function. This generalization includes generalizations of the inverse function theorem and the implicit function theorem, where the non-nullity of the derivative is replaced by the non-nullity of the Jacobian determinant, and the multiplicative inverse of the derivative is replaced by the inverse of the Jacobian matrix. The Jacobian determinant is fundamentally used f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplier (economics)
In macroeconomics, a multiplier is a factor of proportionality that measures how much an endogenous variable changes in response to a change in some exogenous variable. For example, suppose variable ''x'' changes by ''k'' units, which causes another variable ''y'' to change by ''M'' × ''k'' units. Then the multiplier is ''M''. Common uses Two multipliers are commonly discussed in introductory macroeconomics. Commercial banks create money, especially under the fractional-reserve banking system used throughout the world. In this system, money is created whenever a bank gives out a new loan. This is because the loan, when drawn on and spent, mostly finishes up as a deposit back in the banking system and is counted as part of money supply. After putting aside a part of these deposits as mandated bank reserves, the balance is available for the making of further loans by the bank. This process continues multiple times, and is called the multiplier effect. The multiplier m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |