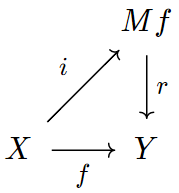|
Cofibration
In mathematics, in particular homotopy theory, a continuous mapping between topological spaces :i: A \to X, is a ''cofibration'' if it has the homotopy extension property with respect to all topological spaces S. That is, i is a cofibration if for each topological space S, and for any continuous maps f, f': A\to S and g:X\to S with g\circ i=f, for any homotopy h : A\times I\to S from f to f', there is a continuous map g':X \to S and a homotopy h': X\times I \to S from g to g' such that h'(i(a),t)=h(a,t) for all a\in A and t\in I. (Here, I denotes the unit interval ,1/math>.) This definition is formally dual to that of a fibration, which is required to satisfy the homotopy lifting property with respect to all spaces; this is one instance of the broader Eckmann–Hilton duality in topology. Cofibrations are a fundamental concept of homotopy theory. Quillen has proposed the notion of model category as a formal framework for doing homotopy theory in more general categories; a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cofibration Diagram
In mathematics, in particular homotopy theory, a continuous mapping between topological spaces :i: A \to X, is a ''cofibration'' if it has the homotopy extension property with respect to all topological spaces S. That is, i is a cofibration if for each topological space S, and for any continuous maps f, f': A\to S and g:X\to S with g\circ i=f, for any homotopy h : A\times I\to S from f to f', there is a continuous map g':X \to S and a homotopy h': X\times I \to S from g to g' such that h'(i(a),t)=h(a,t) for all a\in A and t\in I. (Here, I denotes the unit interval ,1/math>.) This definition is formally dual to that of a fibration, which is required to satisfy the homotopy lifting property with respect to all spaces; this is one instance of the broader Eckmann–Hilton duality in topology. Cofibrations are a fundamental concept of homotopy theory. Quillen has proposed the notion of model category as a formal framework for doing homotopy theory in more general categories; a model ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Theory
In mathematics, homotopy theory is a systematic study of situations in which Map (mathematics), maps can come with homotopy, homotopies between them. It originated as a topic in algebraic topology, but nowadays is learned as an independent discipline. Applications to other fields of mathematics Besides algebraic topology, the theory has also been used in other areas of mathematics such as: * Algebraic geometry (e.g., A1 homotopy theory, A1 homotopy theory) * Category theory (specifically the study of higher category theory, higher categories) Concepts Spaces and maps In homotopy theory and algebraic topology, the word "space" denotes a topological space. In order to avoid Pathological (mathematics), pathologies, one rarely works with arbitrary spaces; instead, one requires spaces to meet extra constraints, such as being Category of compactly generated weak Hausdorff spaces, compactly generated weak Hausdorff or a CW complex. In the same vein as above, a "Map (mathematics), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mapping Cylinder
In mathematics, specifically algebraic topology, the mapping cylinder of a continuous function f between topological spaces X and Y is the quotient :M_f = (( ,1times X) \amalg Y)\,/\,\sim where the \amalg denotes the disjoint union, and ~ is the equivalence relation generated by :(0,x)\sim f(x)\quad\textx\in X. That is, the mapping cylinder M_f is obtained by gluing one end of X\times ,1/math> to Y via the map f. Notice that the "top" of the cylinder \\times X is homeomorphic to X, while the "bottom" is the space f(X)\subset Y. It is common to write Mf for M_f, and to use the notation \sqcup_f or \cup_f for the mapping cylinder construction. That is, one writes :Mf = ( ,1times X) \cup_f Y with the subscripted cup symbol denoting the equivalence. The mapping cylinder is commonly used to construct the mapping cone Cf, obtained by collapsing one end of the cylinder to a point. Mapping cylinders are central to the definition of cofibrations. Basic properties The bottom ''Y'' is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deformation Retract
In topology, a retraction is a continuous mapping from a topological space into a subspace that preserves the position of all points in that subspace. The subspace is then called a retract of the original space. A deformation retraction is a mapping that captures the idea of ''continuously shrinking'' a space into a subspace. An absolute neighborhood retract (ANR) is a particularly well-behaved type of topological space. For example, every topological manifold is an ANR. Every ANR has the homotopy type of a very simple topological space, a CW complex. Definitions Retract Let ''X'' be a topological space and ''A'' a subspace of ''X''. Then a continuous map :r\colon X \to A is a retraction if the restriction of ''r'' to ''A'' is the identity map on ''A''; that is, r(a) = a for all ''a'' in ''A''. Equivalently, denoting by :\iota\colon A \hookrightarrow X the inclusion, a retraction is a continuous map ''r'' such that :r \circ \iota = \operatorname_A, that is, the composition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Extension Property
In mathematics, in the area of algebraic topology, the homotopy extension property indicates which homotopies defined on a subspace can be extended to a homotopy defined on a larger space. The homotopy extension property of cofibrations is dual to the homotopy lifting property that is used to define fibrations. Definition Let X\,\! be a topological space In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a to ..., and let A \subset X. We say that the pair (X,A)\,\! has the homotopy extension property if, given a homotopy f_\bullet\colon A \rightarrow Y^I and a map \tilde_0\colon X \rightarrow Y such that \tilde_0\circ \iota = \left.\tilde_0\_A = f_0 = \pi_0 \circ f_\bullet, then there exists an ''extension'' of f_\bullet to a homotopy \tilde_\bullet\colon X \rightarrow Y^I such that \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eckmann–Hilton Duality
In the mathematical disciplines of algebraic topology and homotopy theory, Eckmann–Hilton duality in its most basic form, consists of taking a given diagram for a particular concept and reversing the direction of all arrows, much as in category theory with the idea of the opposite category. A significantly deeper form argues that the fact that the dual notion of a limit is a colimit allows us to change the Eilenberg–Steenrod axioms for homology to give axioms for cohomology. It is named after Beno Eckmann and Peter Hilton. Discussion An example is given by currying, which tells us that for any object X, a map X \times I \to Y is the same as a map X \to Y^I, where Y^I is the exponential object, given by all maps from I to Y . In the case of topological spaces, if we take I to be the unit interval, this leads to a duality between X \times I and Y^I, which then gives a duality between the reduced suspension \Sigma X, which is a quotient of X \times I, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibration
The notion of a fibration generalizes the notion of a fiber bundle and plays an important role in algebraic topology, a branch of mathematics. Fibrations are used, for example, in Postnikov systems or obstruction theory. In this article, all mappings are continuous mappings between topological spaces. Formal definitions Homotopy lifting property A mapping p \colon E \to B satisfies the homotopy lifting property for a space X if: * for every homotopy h \colon X \times , 1\to B and * for every mapping (also called lift) \tilde h_0 \colon X \to E lifting h, _ = h_0 (i.e. h_0 = p \circ \tilde h_0) there exists a (not necessarily unique) homotopy \tilde h \colon X \times , 1\to E lifting h (i.e. h = p \circ \tilde h) with \tilde h_0 = \tilde h, _. The following commutative diagram shows the situation: Fibration A fibration (also called Hurewicz fibration) is a mapping p \colon E \to B satisfying the homotopy lifting property for all spaces X. The space B is called base ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Colimit
In topology, two continuous functions from one topological space to another are called homotopic (from and ) if one can be "continuously deformed" into the other, such a deformation being called a homotopy ( ; ) between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology. In practice, there are technical difficulties in using homotopies with certain spaces. Algebraic topologists work with compactly generated spaces, CW complexes, or spectra. Formal definition Formally, a homotopy between two continuous functions ''f'' and ''g'' from a topological space ''X'' to a topological space ''Y'' is defined to be a continuous function H: X \times ,1\to Y from the product of the space ''X'' with the unit interval , 1to ''Y'' such that H(x,0) = f(x) and H(x,1) = g(x) for all x \in X. If we think of the second parameter of ''H'' as time then ''H'' describes a ''cont ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic (from and ) if one can be "continuously deformed" into the other, such a deformation being called a homotopy ( ; ) between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology. In practice, there are technical difficulties in using homotopies with certain spaces. Algebraic topologists work with compactly generated spaces, CW complexes, or spectra. Formal definition Formally, a homotopy between two continuous functions ''f'' and ''g'' from a topological space ''X'' to a topological space ''Y'' is defined to be a continuous function H: X \times ,1\to Y from the product of the space ''X'' with the unit interval , 1to ''Y'' such that H(x,0) = f(x) and H(x,1) = g(x) for all x \in X. If we think of the second parameter of ''H'' as time then ''H'' describes a ''continu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cofiber Sequence
In mathematics, the Puppe sequence is a construction of homotopy theory, so named after Dieter Puppe. It comes in two forms: a long exact sequence, built from the mapping fibre (a fibration), and a long coexact sequence, built from the mapping cone (which is a cofibration). Joseph J. Rotman, ''An Introduction to Algebraic Topology'' (1988) Springer-Verlag ''(See Chapter 11 for construction.)'' Intuitively, the Puppe sequence allows us to think of homology theory as a functor that takes spaces to long-exact sequences of groups. It is also useful as a tool to build long exact sequences of relative homotopy groups. Exact Puppe sequence A sequence of pointed spaces and pointed maps \dots \to X_ \to X_n \to X_ \to \dots is called exact if the induced sequence \dots \to , X_\to , X_n\to , X_\to \dots is exact as a sequence of pointed sets (taking the kernel of a map to be those elements mapped to the basepoint) for every pointed space Z. Let f\colon (X,x_0)\to(Y,y_0) be a contin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |