|
Closed-loop Pole
In systems theory, closed-loop poles are the positions of the poles (or eigenvalues) of a closed-loop transfer function in the s-plane. The open-loop transfer function is equal to the product of all transfer function blocks in the forward path in the block diagram. The closed-loop transfer function is obtained by dividing the open-loop transfer function by the sum of one and the product of all transfer function blocks throughout the negative feedback loop. The closed-loop transfer function may also be obtained by algebraic or block diagram manipulation. Once the closed-loop transfer function is obtained for the system, the closed-loop poles are obtained by solving the characteristic equation. The characteristic equation is nothing more than setting the denominator of the closed-loop transfer function to zero. In control theory there are two main methods of analyzing feedback systems: the transfer function (or frequency domain) method and the state space method. When the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Systems Theory
Systems theory is the interdisciplinary study of systems, i.e. cohesive groups of interrelated, interdependent components that can be natural or human-made. Every system has causal boundaries, is influenced by its context, defined by its structure, function and role, and expressed through its relations with other systems. A system is "more than the sum of its parts" by expressing synergy or emergent behavior. Changing one component of a system may affect other components or the whole system. It may be possible to predict these changes in patterns of behavior. For systems that learn and adapt, the growth and the degree of adaptation depend upon how well the system is engaged with its environment and other contexts influencing its organization. Some systems support other systems, maintaining the other system to prevent failure. The goals of systems theory are to model a system's dynamics, constraints, conditions, and relations; and to elucidate principles (such as purpose, meas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Impulse Response
In signal processing and control theory, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse (). More generally, an impulse response is the reaction of any dynamic system in response to some external change. In both cases, the impulse response describes the reaction of the system as a function of time (or possibly as a function of some other independent variable that parameterizes the dynamic behavior of the system). In all these cases, the dynamic system and its impulse response may be actual physical objects, or may be mathematical systems of equations describing such objects. Since the impulse function contains all frequencies (see the Fourier transform of the Dirac delta function, showing infinite frequency bandwidth that the Dirac delta function has), the impulse response defines the response of a linear time-invariant system for all frequencies. Mathematical considerat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plant (control Theory)
A plant in control theory is the combination of process and actuator. A plant is often referred to with a transfer function (commonly in the s-domain) which indicates the relation between an input signal and the output signal of a system without feedback, commonly determined by physical properties of the system. An example would be an actuator An actuator is a component of a machine that is responsible for moving and controlling a mechanism or system, for example by opening a valve. In simple terms, it is a "mover". An actuator requires a control device (controlled by control signal) a ... with its transfer of the input of the actuator to its physical displacement. In a system with feedback, the plant still has the same transfer function, but a control unit and a feedback loop (with their respective transfer functions) are added to the system. References * * * Classical control theory Control loop theory Cybernetics {{Systemstheory-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
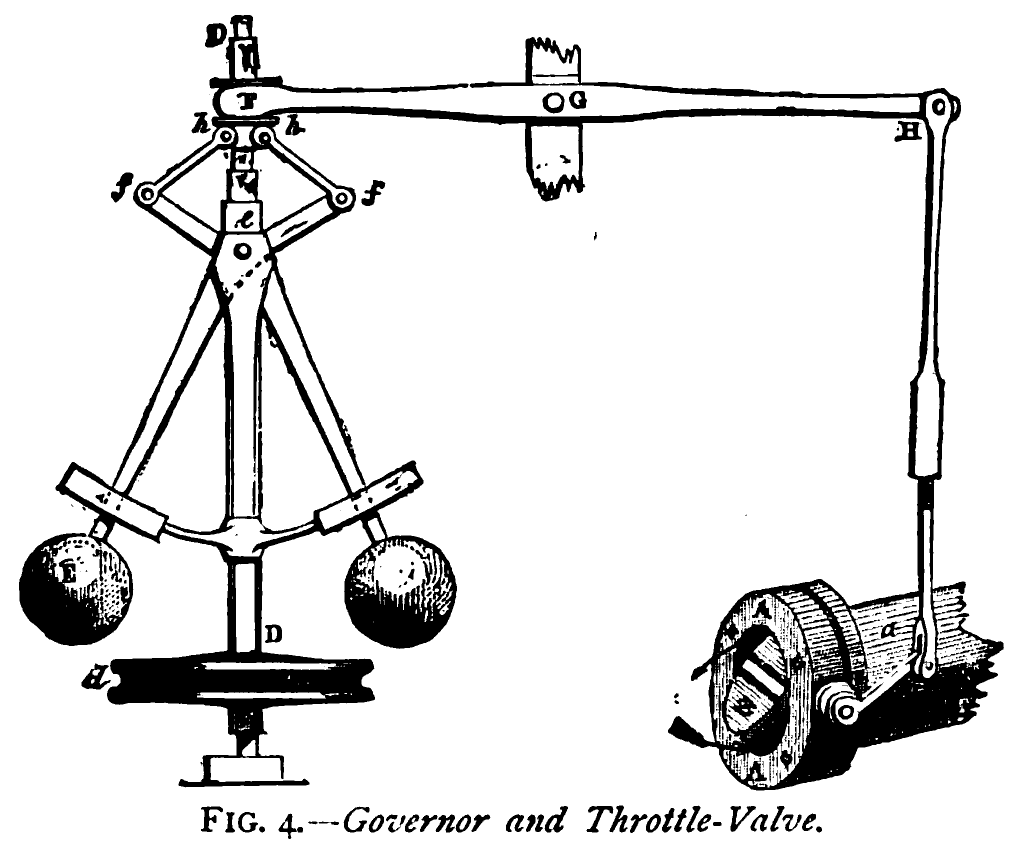
Proportional Control
Proportional control, in engineering and process control, is a type of linear feedback control system in which a correction is applied to the controlled variable, and the size of the correction is proportional to the difference between the desired value ( setpoint, SP) and the measured value ( process variable, PV). Two classic mechanical examples are the toilet bowl float proportioning valve and the fly-ball governor. The proportional control concept is more complex than an on–off control system such as a bi-metallic domestic thermostat, but simpler than a proportional–integral–derivative (PID) control system used in something like an automobile cruise control. On–off control will work where the overall system has a relatively long response time, but can result in instability if the system being controlled has a rapid response time. Proportional control overcomes this by modulating the output to the controlling device, such as a control valve at a level which avoi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Negative Feedback
Negative feedback (or balancing feedback) occurs when some function of the output of a system, process, or mechanism is fed back in a manner that tends to reduce the fluctuations in the output, whether caused by changes in the input or by other disturbances. Whereas positive feedback tends to lead to instability via exponential growth, oscillation or chaotic behavior, negative feedback generally promotes stability. Negative feedback tends to promote a settling to equilibrium, and reduces the effects of perturbations. Negative feedback loops in which just the right amount of correction is applied with optimum timing can be very stable, accurate, and responsive. Negative feedback is widely used in mechanical and electronic engineering, and also within living organisms, and can be seen in many other fields from chemistry and economics to physical systems such as the climate. General negative feedback systems are studied in control systems engineering. Negative feedback l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnitude Condition
In control theory and stability theory, root locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter, commonly a gain within a feedback system. This is a technique used as a stability criterion in the field of classical control theory developed by Walter R. Evans which can determine stability of the system. The root locus plots the poles of the closed loop transfer function in the complex ''s''-plane as a function of a gain parameter (see pole–zero plot). An analog computer called a "Spirule" can compute root loci. Uses In addition to determining the stability of the system, the root locus can be used to design the damping ratio (''ζ'') and natural frequency (''ω''''n'') of a feedback system. Lines of constant damping ratio can be drawn radially from the origin and lines of constant natural frequency can be drawn as arccosine whose center points coincide with the origin. By selecting a point along ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle Condition
In control theory and stability theory, root locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter, commonly a gain within a feedback system. This is a technique used as a stability criterion in the field of classical control theory developed by Walter R. Evans which can determine stability of the system. The root locus plots the poles of the closed loop transfer function in the complex ''s''-plane as a function of a gain parameter (see pole–zero plot). Evans also invented in 1948 an analog computer to compute root loci, called a "Spirule" (after "spiral" and "slide rule"); it found wide use before the advent of digital computers. Uses In addition to determining the stability of the system, the root locus can be used to design the damping ratio (''ζ'') and natural frequency (''ω''''n'') of a feedback system. Lines of constant damping ratio can be drawn radially from the origin and lines of constant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gain (electronics)
In electronics, gain is a measure of the ability of a two-port circuit (often an amplifier) to increase the power or amplitude of a signal from the input to the output port by adding energy converted from some power supply to the signal. It is usually defined as the mean ratio of the signal amplitude or power at the output port to the amplitude or power at the input port. It is often expressed using the logarithmic decibel (dB) units ("dB gain"). A gain greater than one (greater than zero dB), that is amplification, is the defining property of an active component or circuit, while a passive circuit will have a gain of less than one. The term ''gain'' alone is ambiguous, and can refer to the ratio of output to input voltage (''voltage gain''), current (''current gain'') or electric power (''power gain''). In the field of audio and general purpose amplifiers, especially operational amplifiers, the term usually refers to voltage gain, but in radio frequency amplifiers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steady-state Response
In electronics, steady state is an equilibrium condition of a circuit or network that occurs as the effects of transients are no longer important. Steady state is reached (attained) after transient (initial, oscillating or turbulent) state has subsided. During steady state, a system is in relative stability. Steady state determination is an important topic, because many design specifications of electronic systems are given in terms of the steady-state characteristics. Periodic steady-state solution is also a prerequisite for small signal dynamic modeling. Steady-state analysis is therefore an indispensable component of the design process. Calculation methods Steady state calculation methods can be sorted into time-domain algorithms (time domain sensitivities, shooting) and frequency-domain algorithms (harmonic balance) methods, are the best choice for most microwave circuits excited with sinusoidal signals (e.g. mixers, power amplifiers). Time domain methods Time domain metho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transient Response
In electrical engineering and mechanical engineering, a transient response is the response of a system to a change from an equilibrium or a steady state. The transient response is not necessarily tied to abrupt events but to any event that affects the equilibrium of the system. The impulse response and step response are transient responses to a specific input (an impulse and a step, respectively). In electrical engineering specifically, the transient response is the circuit’s temporary response that will die out with time. It is followed by the steady state response, which is the behavior of the circuit a long time after an external excitation is applied. Damping The response can be classified as one of three types of damping that describes the output in relation to the steady-state response. ;Underdamped :An underdamped response is one that oscillates within a decaying envelope. The more underdamped the system, the more oscillations and longer it takes to reach steady- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |