|
Bigram
A bigram or digram is a sequence of two adjacent elements from a string of tokens, which are typically letters, syllables, or words. A bigram is an ''n''-gram for ''n''=2. The frequency distribution of every bigram in a string is commonly used for simple statistical analysis of text in many applications, including in computational linguistics, cryptography, speech recognition, and so on. ''Gappy bigrams'' or ''skipping bigrams'' are word pairs which allow gaps (perhaps avoiding connecting words, or allowing some simulation of dependencies, as in a dependency grammar). ''Head word bigrams'' are gappy bigrams with an explicit dependency relationship. Details Bigrams help provide the conditional probability of a token given the preceding token, when the relation of the conditional probability is applied: P(W_n, W_) = That is, the probability P() of a token W_n given the preceding token W_ is equal to the probability of their bigram, or the co-occurrence of the two tokens P( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
N-gram
In the fields of computational linguistics and probability, an ''n''-gram (sometimes also called Q-gram) is a contiguous sequence of ''n'' items from a given sample of text or speech. The items can be phonemes, syllables, letters, words or base pairs according to the application. The ''n''-grams typically are collected from a text or speech corpus. When the items are words, -grams may also be called ''shingles''. Using Latin numerical prefixes, an ''n''-gram of size 1 is referred to as a "unigram"; size 2 is a " bigram" (or, less commonly, a "digram"); size 3 is a "trigram". English cardinal numbers are sometimes used, e.g., "four-gram", "five-gram", and so on. In computational biology, a polymer or oligomer of a known size is called a ''k''-mer instead of an ''n''-gram, with specific names using Greek numerical prefixes such as "monomer", "dimer", "trimer", "tetramer", "pentamer", etc., or English cardinal numbers, "one-mer", "two-mer", "three-mer", etc. Applicat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
N-gram
In the fields of computational linguistics and probability, an ''n''-gram (sometimes also called Q-gram) is a contiguous sequence of ''n'' items from a given sample of text or speech. The items can be phonemes, syllables, letters, words or base pairs according to the application. The ''n''-grams typically are collected from a text or speech corpus. When the items are words, -grams may also be called ''shingles''. Using Latin numerical prefixes, an ''n''-gram of size 1 is referred to as a "unigram"; size 2 is a " bigram" (or, less commonly, a "digram"); size 3 is a "trigram". English cardinal numbers are sometimes used, e.g., "four-gram", "five-gram", and so on. In computational biology, a polymer or oligomer of a known size is called a ''k''-mer instead of an ''n''-gram, with specific names using Greek numerical prefixes such as "monomer", "dimer", "trimer", "tetramer", "pentamer", etc., or English cardinal numbers, "one-mer", "two-mer", "three-mer", etc. Applicat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Analysis (cryptanalysis)
In cryptanalysis, frequency analysis (also known as counting letters) is the study of the frequency of letters or groups of letters in a ciphertext. The method is used as an aid to breaking classical ciphers. Frequency analysis is based on the fact that, in any given stretch of written language, certain letters and combinations of letters occur with varying frequencies. Moreover, there is a characteristic distribution of letters that is roughly the same for almost all samples of that language. For instance, given a section of English language, , , and are the most common, while , , and are rare. Likewise, , , , and are the most common pairs of letters (termed ''bigrams'' or ''digraphs''), and , , , and are the most common repeats. The nonsense phrase " ETAOIN SHRDLU" represents the 12 most frequent letters in typical English language text. In some ciphers, such properties of the natural language plaintext are preserved in the ciphertext, and these patterns have the poten ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sørensen–Dice Coefficient
The Sørensen–Dice coefficient (see below for other names) is a statistic used to gauge the similarity of two samples. It was independently developed by the botanists Thorvald Sørensen and Lee Raymond Dice, who published in 1948 and 1945 respectively. Name The index is known by several other names, especially Sørensen–Dice index, Sørensen index and Dice's coefficient. Other variations include the "similarity coefficient" or "index", such as Dice similarity coefficient (DSC). Common alternate spellings for Sørensen are ''Sorenson'', ''Soerenson'' and ''Sörenson'', and all three can also be seen with the ''–sen'' ending. Other names include: * F1 score * Czekanowski's binary (non-quantitative) index * Measure of genetic similarity * Zijdenbos similarity index, referring to a 1994 paper of Zijdenbos et al. Formula Sørensen's original formula was intended to be applied to discrete data. Given two sets, X and Y, it is defined as : DSC = \frac where , ''X'', and , ''Y' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Language Model
A language model is a probability distribution over sequences of words. Given any sequence of words of length , a language model assigns a probability P(w_1,\ldots,w_m) to the whole sequence. Language models generate probabilities by training on text corpora in one or many languages. Given that languages can be used to express an infinite variety of valid sentences (the property of digital infinity), language modeling faces the problem of assigning non-zero probabilities to linguistically valid sequences that may never be encountered in the training data. Several modelling approaches have been designed to surmount this problem, such as applying the Markov assumption or using neural architectures such as recurrent neural networks or transformers. Language models are useful for a variety of problems in computational linguistics; from initial applications in speech recognition to ensure nonsensical (i.e. low-probability) word sequences are not predicted, to wider use in machine tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Letter Frequency
Letter frequency is the number of times letters of the alphabet appear on average in written language. Letter frequency analysis dates back to the Arab mathematician Al-Kindi (c. 801–873 AD), who formally developed the method to break ciphers. Letter frequency analysis gained importance in Europe with the development of movable type in 1450 AD, where one must estimate the amount of type required for each letterform. Linguists use letter frequency analysis as a rudimentary technique for language identification, where it is particularly effective as an indication of whether an unknown writing system is alphabetic, syllabic, or ideographic. The use of letter frequencies and frequency analysis plays a fundamental role in cryptograms and several word puzzle games, including Hangman, '' Scrabble'', '' Wordle'' and the television game show ''Wheel of Fortune''. One of the earliest descriptions in classical literature of applying the knowledge of English letter frequenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logology (linguistics)
Logology (or ludolinguistics) is the field of recreational linguistics, an activity that encompasses a wide variety of word games and wordplay. The term is analogous to the term "recreational mathematics". Overview Some of the topics studied in logology are lipograms, acrostics, palindromes, tautonyms, isograms, pangrams, bigrams, trigrams, tetragrams, transdeletion pyramids, and pangrammatic windows. The term ''logology'' was adopted by Dmitri Borgmann to refer to recreational linguistics. Notable logologists *Dmitri Borgmann * A. Ross Eckler, Jr. *Willard R. Espy *Jeremiah Farrell *Martin Gardner * Mike Keith *Douglas Hofstadter See also *Constrained writing * List of forms of word play *Oulipo *'' Word Ways: The Journal of Recreational Linguistics'' References Bibliography Books * * * * * * {{cite encyclopedia , last1=Johnson , first1=Dale D. , last2=von Hoff Johnson , first2=Bonnie , last3=Schlichting , first3=Kathleen , editor1-last=Baumann , editor1-first=James ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
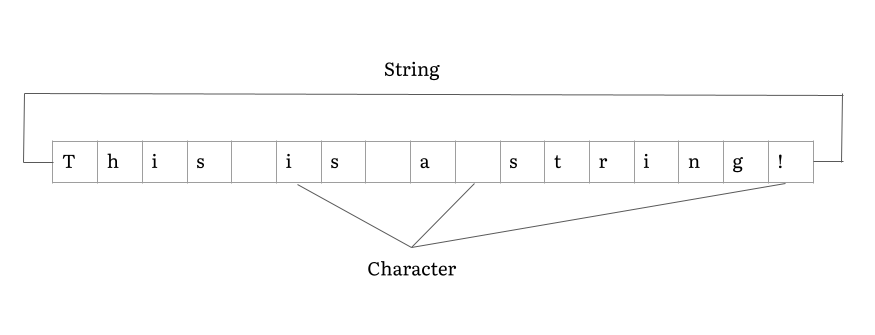
String (computer Science)
In computer programming, a string is traditionally a sequence of characters, either as a literal constant or as some kind of variable. The latter may allow its elements to be mutated and the length changed, or it may be fixed (after creation). A string is generally considered as a data type and is often implemented as an array data structure of bytes (or words) that stores a sequence of elements, typically characters, using some character encoding. ''String'' may also denote more general arrays or other sequence (or list) data types and structures. Depending on the programming language and precise data type used, a variable declared to be a string may either cause storage in memory to be statically allocated for a predetermined maximum length or employ dynamic allocation to allow it to hold a variable number of elements. When a string appears literally in source code, it is known as a string literal or an anonymous string. In formal languages, which are used in ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Languages
In logic, mathematics, computer science, and linguistics, a formal language consists of words whose letters are taken from an alphabet and are well-formed according to a specific set of rules. The alphabet of a formal language consists of symbols, letters, or tokens that concatenate into strings of the language. Each string concatenated from symbols of this alphabet is called a word, and the words that belong to a particular formal language are sometimes called ''well-formed words'' or '' well-formed formulas''. A formal language is often defined by means of a formal grammar such as a regular grammar or context-free grammar, which consists of its formation rules. In computer science, formal languages are used among others as the basis for defining the grammar of programming languages and formalized versions of subsets of natural languages in which the words of the language represent concepts that are associated with particular meanings or semantics. In computational com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digraph (orthography)
A digraph or digram (from the grc, δίς , "double" and , "to write") is a pair of characters used in the orthography of a language to write either a single phoneme (distinct sound), or a sequence of phonemes that does not correspond to the normal values of the two characters combined. Some digraphs represent phonemes that cannot be represented with a single character in the writing system of a language, like the English '' sh'' in ''ship'' and ''fish''. Other digraphs represent phonemes that can also be represented by single characters. A digraph that shares its pronunciation with a single character may be a relic from an earlier period of the language when the digraph had a different pronunciation, or may represent a distinction that is made only in certain dialects, like the English '' wh''. Some such digraphs are used for purely etymological reasons, like '' rh'' in English. Digraphs are used in some Romanization schemes, like the '' zh'' often used to represent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cryptograms
A cryptogram is a type of puzzle that consists of a short piece of encrypted text. Generally the cipher used to encrypt the text is simple enough that the cryptogram can be solved by hand. Substitution ciphers where each letter is replaced by a different letter or number are frequently used. To solve the puzzle, one must recover the original lettering. Though once used in more serious applications, they are now mainly printed for entertainment in newspapers and magazines. Other types of classical ciphers are sometimes used to create cryptograms. An example is the book cipher where a book or article is used to encrypt a message. History of cryptograms The ciphers used in cryptograms were not originally created for entertainment purposes, but for real encryption of military or personal secrets. The first use of the cryptogram for entertainment purposes occurred during the Middle Ages by monks who had spare time for intellectual games. A manuscript found at Bamberg states tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Language Detection
In natural language processing, language identification or language guessing is the problem of determining which natural language given content is in. Computational approaches to this problem view it as a special case of text categorization, solved with various statistical methods. Overview There are several statistical approaches to language identification using different techniques to classify the data. One technique is to compare the compressibility of the text to the compressibility of texts in a set of known languages. This approach is known as mutual information based distance measure. The same technique can also be used to empirically construct family trees of languages which closely correspond to the trees constructed using historical methods. Mutual information based distance measure is essentially equivalent to more conventional model-based methods and is not generally considered to be either novel or better than simpler techniques. Another technique, as describe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |