|
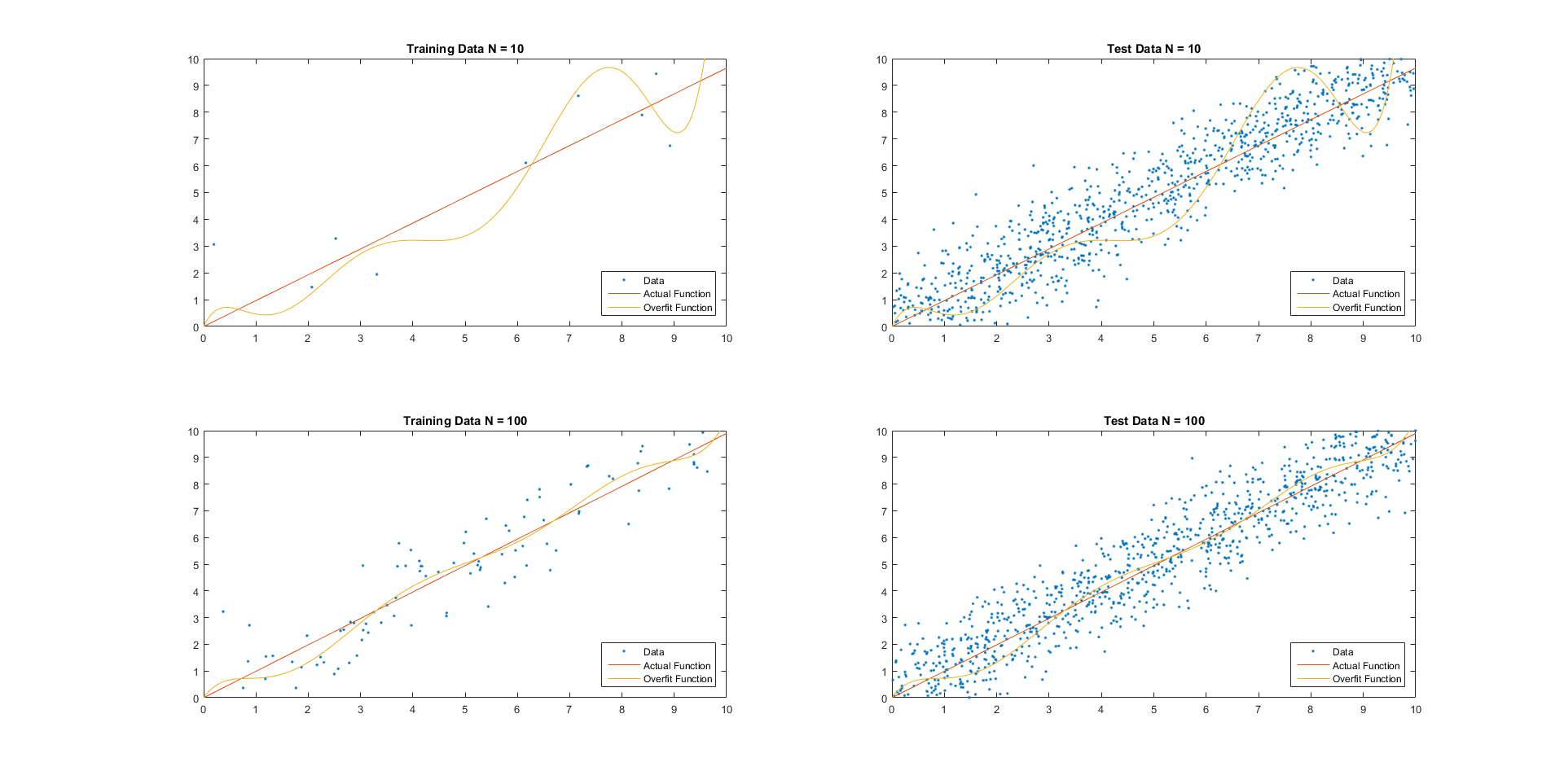
Bias–variance Tradeoff
In statistics and machine learning, the bias–variance tradeoff is the property of a model that the variance of the parameter estimated across samples can be reduced by increasing the bias in the estimated parameters. The bias–variance dilemma or bias–variance problem is the conflict in trying to simultaneously minimize these two sources of error that prevent supervised learning algorithms from generalizing beyond their training set: * The ''bias'' error is an error from erroneous assumptions in the learning algorithm. High bias can cause an algorithm to miss the relevant relations between features and target outputs (underfitting). * The ''variance'' is an error from sensitivity to small fluctuations in the training set. High variance may result from an algorithm modeling the random noise in the training data (overfitting). The bias–variance decomposition is a way of analyzing a learning algorithm's expected generalization error with respect to a particular proble ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radial Basis Functions
A radial basis function (RBF) is a real-valued function \varphi whose value depends only on the distance between the input and some fixed point, either the origin, so that \varphi(\mathbf) = \hat\varphi(\left\, \mathbf\right\, ), or some other fixed point \mathbf, called a ''center'', so that \varphi(\mathbf) = \hat\varphi(\left\, \mathbf-\mathbf\right\, ). Any function \varphi that satisfies the property \varphi(\mathbf) = \hat\varphi(\left\, \mathbf\right\, ) is a radial function. The distance is usually Euclidean distance, although other metrics are sometimes used. They are often used as a collection \_k which forms a basis for some function space of interest, hence the name. Sums of radial basis functions are typically used to approximate given functions. This approximation process can also be interpreted as a simple kind of neural network; this was the context in which they were originally applied to machine learning, in work by David Broomhead and David Lowe in 1988, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalization Error
For supervised learning applications in machine learning and statistical learning theory, generalization error (also known as the out-of-sample error or the risk) is a measure of how accurately an algorithm is able to predict outcome values for previously unseen data. Because learning algorithms are evaluated on finite samples, the evaluation of a learning algorithm may be sensitive to sampling error. As a result, measurements of prediction error on the current data may not provide much information about predictive ability on new data. Generalization error can be minimized by avoiding overfitting in the learning algorithm. The performance of a machine learning algorithm is visualized by plots that show values of ''estimates'' of the generalization error through the learning process, which are called learning curves. Definition In a learning problem, the goal is to develop a function f_n(\vec) that predicts output values y for each input datum \vec. The subscript n indicates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of Edinburgh
The University of Edinburgh ( sco, University o Edinburgh, gd, Oilthigh Dhùn Èideann; abbreviated as ''Edin.'' in post-nominals) is a public research university based in Edinburgh, Scotland. Granted a royal charter by King James VI in 1582 and officially opened in 1583, it is one of Scotland's four ancient universities and the sixth-oldest university in continuous operation in the English-speaking world. The university played an important role in Edinburgh becoming a chief intellectual centre during the Scottish Enlightenment and contributed to the city being nicknamed the " Athens of the North." Edinburgh is ranked among the top universities in the United Kingdom and the world. Edinburgh is a member of several associations of research-intensive universities, including the Coimbra Group, League of European Research Universities, Russell Group, Una Europa, and Universitas 21. In the fiscal year ending 31 July 2021, it had a total income of £1.176 billion, of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Model
In statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However, the term is also used in time series analysis with a different meaning. In each case, the designation "linear" is used to identify a subclass of models for which substantial reduction in the complexity of the related statistical theory is possible. Linear regression models For the regression case, the statistical model is as follows. Given a (random) sample (Y_i, X_, \ldots, X_), \, i = 1, \ldots, n the relation between the observations Y_i and the independent variables X_ is formulated as :Y_i = \beta_0 + \beta_1 \phi_1(X_) + \cdots + \beta_p \phi_p(X_) + \varepsilon_i \qquad i = 1, \ldots, n where \phi_1, \ldots, \phi_p may be nonlinear functions. In the above, the quantities \varepsilon_i are random variables representing errors in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bootstrapping (statistics)
Bootstrapping is any test or metric that uses random sampling with replacement (e.g. mimicking the sampling process), and falls under the broader class of resampling methods. Bootstrapping assigns measures of accuracy (bias, variance, confidence intervals, prediction error, etc.) to sample estimates.software This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods. Bootstrapping estimates the properties of an estimand (such as its variance) by measuring those properties when sampling from an approximating distribution. One standard choice for an approximating distribution is the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Squared Error
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss. The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate. In machine learning, specifically empirical risk minimization, MSE may refer to the ''empirical'' risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution). The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shrinkage (statistics)
In statistics, shrinkage is the reduction in the effects of sampling variation. In regression analysis, a fitted relationship appears to perform less well on a new data set than on the data set used for fitting. In particular the value of the coefficient of determination 'shrinks'. This idea is complementary to overfitting and, separately, to the standard adjustment made in the coefficient of determination to compensate for the subjunctive effects of further sampling, like controlling for the potential of new explanatory terms improving the model by chance: that is, the adjustment formula itself provides "shrinkage." But the adjustment formula yields an artificial shrinkage. A shrinkage estimator is an estimator that, either explicitly or implicitly, incorporates the effects of shrinkage. In loose terms this means that a naive or raw estimate is improved by combining it with other information. The term relates to the notion that the improved estimate is made closer to the value ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regularization (mathematics)
In mathematics, statistics, finance, computer science, particularly in machine learning and inverse problems, regularization is a process that changes the result answer to be "simpler". It is often used to obtain results for ill-posed problems or to prevent overfitting. Although regularization procedures can be divided in many ways, following delineation is particularly helpful: * Explicit regularization is regularization whenever one explicitly adds a term to the optimization problem. These terms could be priors, penalties, or constraints. Explicit regularization is commonly employed with ill-posed optimization problems. The regularization term, or penalty, imposes a cost on the optimization function to make the optimal solution unique. * Implicit regularization is all other forms of regularization. This includes, for example, early stopping, using a robust loss function, and discarding outliers. Implicit regularization is essentially ubiquitous in modern machine learning app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smoothing
In statistics and image processing, to smooth a data set is to create an approximating function that attempts to capture important patterns in the data, while leaving out noise or other fine-scale structures/rapid phenomena. In smoothing, the data points of a signal are modified so individual points higher than the adjacent points (presumably because of noise) are reduced, and points that are lower than the adjacent points are increased leading to a smoother signal. Smoothing may be used in two important ways that can aid in data analysis (1) by being able to extract more information from the data as long as the assumption of smoothing is reasonable and (2) by being able to provide analyses that are both flexible and robust. Many different algorithms are used in smoothing. Smoothing may be distinguished from the related and partially overlapping concept of curve fitting in the following ways: * curve fitting often involves the use of an explicit function form for the result, where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Training, Validation, And Test Data Sets
In machine learning, a common task is the study and construction of Algorithm, algorithms that can learn from and make predictions on data. Such algorithms function by making data-driven predictions or decisions, through building a mathematical model from input data. These input data used to build the model are usually divided in multiple Data set, data sets. In particular, three data sets are commonly used in different stages of the creation of the model: training, validation and test sets. The model is initially fit on a training data set, which is a set of examples used to fit the parameters (e.g. weights of connections between neurons in artificial neural networks) of the model. The model (e.g. a naive Bayes classifier) is trained on the training data set using a supervised learning method, for example using optimization methods such as gradient descent or stochastic gradient descent. In practice, the training data set often consists of pairs of an input Array data structure, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sample Space
In probability theory, the sample space (also called sample description space, possibility space, or outcome space) of an experiment or random trial is the set of all possible outcomes or results of that experiment. A sample space is usually denoted using set notation, and the possible ordered outcomes, or sample points, are listed as elements in the set. It is common to refer to a sample space by the labels ''S'', Ω, or ''U'' (for " universal set"). The elements of a sample space may be numbers, words, letters, or symbols. They can also be finite, countably infinite, or uncountably infinite. A subset of the sample space is an event, denoted by E. If the outcome of an experiment is included in E, then event E has occurred. For example, if the experiment is tossing a single coin, the sample space is the set \, where the outcome H means that the coin is heads and the outcome T means that the coin is tails. The possible events are E=\, E = \, and E = \. For tossing two coins ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Accuracy And Precision
Accuracy and precision are two measures of ''observational error''. ''Accuracy'' is how close a given set of measurements ( observations or readings) are to their '' true value'', while ''precision'' is how close the measurements are to each other. In other words, ''precision'' is a description of '' random errors'', a measure of statistical variability. ''Accuracy'' has two definitions: # More commonly, it is a description of only ''systematic errors'', a measure of statistical bias of a given measure of central tendency; low accuracy causes a difference between a result and a true value; ISO calls this ''trueness''. # Alternatively, ISO defines accuracy as describing a combination of both types of observational error (random and systematic), so high accuracy requires both high precision and high trueness. In the first, more common definition of "accuracy" above, the concept is independent of "precision", so a particular set of data can be said to be accurate, precise, both, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |