|
Boerdijk–Coxeter Helix
The Boerdijk–Coxeter helix, named after H. S. M. Coxeter and , is a linear stacking of regular tetrahedron, tetrahedra, arranged so that the edges of the complex that belong to only one tetrahedron form three intertwined helix, helices. There are two Chirality (mathematics), chiral forms, with either right-handed or left-handed windings. Unlike any other stacking of Platonic solids, the Boerdijk–Coxeter helix is not rotationally repetitive in 3-dimensional space. Even in an infinite string of stacked tetrahedra, no two tetrahedra will have the same orientation, because the helical pitch per cell is not a rational fraction of the circle. However, modified forms of this helix have been found which are rotationally repetitive, and in 4-dimensional space this helix repeats in rings of exactly 30 tetrahedral cells that tessellate the 3-sphere surface of the 600-cell, one of the six regular convex 4-polytope, polychora. Buckminster Fuller named it a ''tetrahelix'' and considered ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Helix 3 Colors
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century. Coxeter was born in England and educated at the University of Cambridge, with student visits to Princeton University. He worked for 60 years at the University of Toronto in Canada, from 1936 until his retirement in 1996, becoming a full professor there in 1948. His many honours included membership in the Royal Society of Canada, the Royal Society, and the Order of Canada. He was an author of 12 books, including ''The Fifty-Nine Icosahedra'' (1938) and ''Regular Polytopes (book), Regular Polytopes'' (1947). Many concepts in geometry and group theory are named after him, including the Coxeter graph, Coxeter groups, Coxeter's loxodromic sequence of tangent circles, Coxeter–Dynkin diagrams, and the Todd–Coxeter algorithm. Biography Coxeter was born in Kensington, England, to Ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
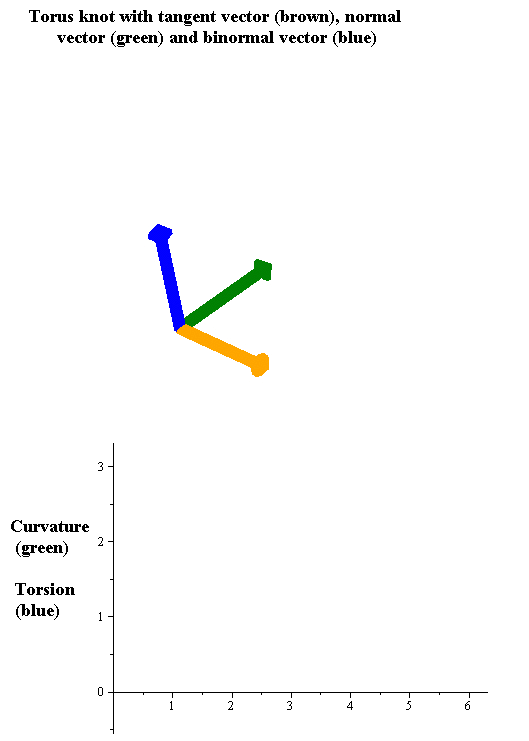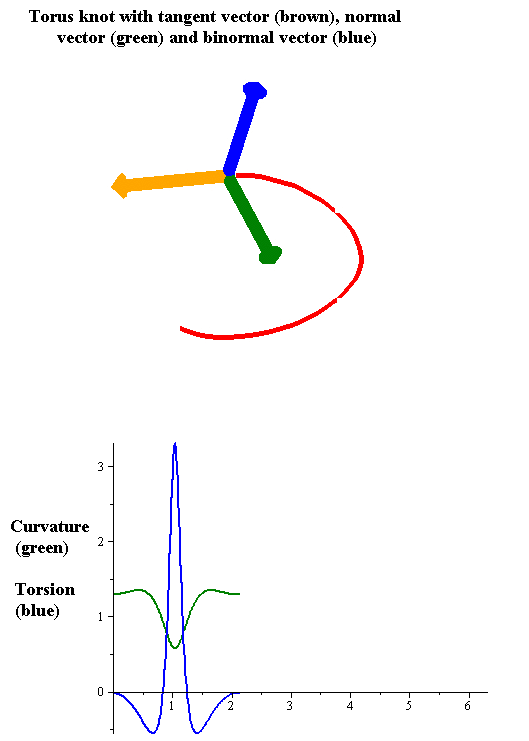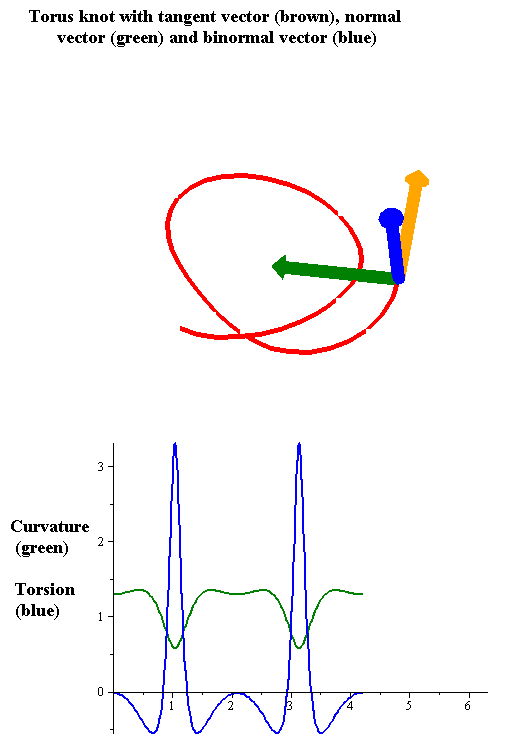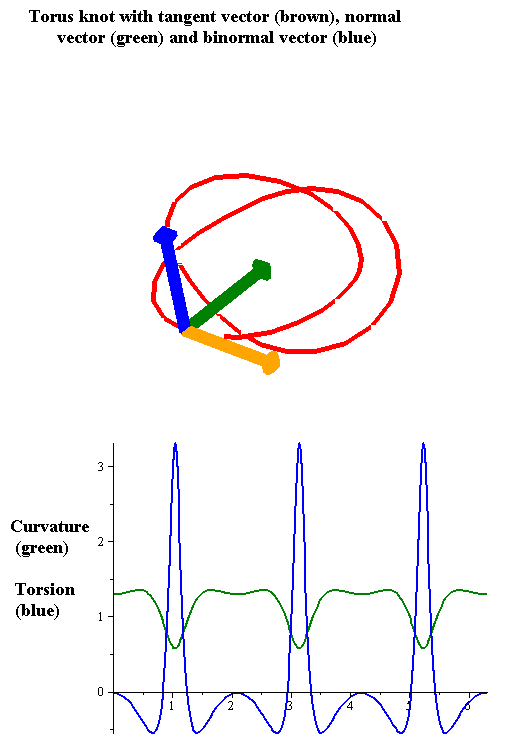
Torsion Of A Curve
In the differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting out of the osculating plane. Taken together, the curvature and the torsion of a space curve are analogous to the curvature of a plane curve. For example, they are coefficients in the system of differential equations for the Frenet frame given by the Frenet–Serret formulas. Definition Let be a space curve parametrized by arc length and with the unit tangent vector . If the curvature of at a certain point is not zero then the principal normal vector and the binormal vector at that point are the unit vectors : \mathbf=\frac, \quad \mathbf=\mathbf\times\mathbf respectively, where the prime denotes the derivative of the vector with respect to the parameter . The torsion measures the speed of rotation of the binormal vector at the given point. It is found from the equation : \mathbf' = -\tau\mathbf. which means : \tau = -\mathbf\cdot\math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Pyramid Helix
In geometry, a square is a regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal sides. As with all rectangles, a square's angles are right angles (90 degrees, or /2 radians), making adjacent sides perpendicular. The area of a square is the side length multiplied by itself, and so in algebra, multiplying a number by itself is called squaring. Equal squares can tile the plane edge-to-edge in the square tiling. Square tilings are ubiquitous in tiled floors and walls, graph paper, image pixels, and game boards. Square shapes are also often seen in building floor plans, origami paper, food servings, in graphic design and heraldry, and in instant photos and fine art. The formula for the area of a square forms the basis of the calculation of area and motivates the search for methods for squaring the circle by compass and straightedge, now ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectified 600-cell
In geometry, the Rectification (geometry), rectified 600-cell or rectified hexacosichoron is a convex uniform 4-polytope composed of 600 regular octahedra and 120 icosahedra cell (mathematics), cells. Each edge has two octahedra and one icosahedron. Each vertex has five octahedra and two icosahedra. In total it has 3600 triangle faces, 3600 edges, and 720 vertices. Containing the cell Hyperplane#Notes, realms of both the regular 120-cell and the regular 600-cell, it can be considered analogous to the polyhedron icosidodecahedron, which is a rectified icosahedron and rectified dodecahedron. The vertex figure of the rectified 600-cell is a uniform pentagonal prism. Semiregular polytope It is one of three Semiregular 4-polytopes#Semiregular polytopes, semiregular 4-polytopes made of two or more cells which are Platonic solids, discovered by Thorold Gosset in his 1900 paper. He called it a ''octicosahedric'' for being made of octahedron and icosahedron cells. Emanuel Lodewijk Elte, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Configuration
In geometry, a vertex configuration is a shorthand notation for representing a polyhedron or Tessellation, tiling as the sequence of Face (geometry), faces around a Vertex (geometry), vertex. It has variously been called a vertex description, vertex type, vertex symbol, vertex arrangement, vertex pattern, face-vector, vertex sequence. It is also called a Cundy and Rollett symbol for its usage for the Archimedean solids in their 1952 book ''Mathematical Models (Cundy and Rollett), Mathematical Models''.Laughlin (2014), p. 16 For uniform polyhedron, uniform polyhedra, there is only one vertex type and therefore the vertex configuration fully defines the polyhedron. (Chirality (mathematics), Chiral polyhedra exist in mirror-image pairs with the same vertex configuration.) For example, "" indicates a vertex belonging to 4 faces, alternating triangles and pentagons. This vertex configuration defines the vertex-transitive icosidodecahedron. The notation is cyclic and therefore is equival ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Pyramid
In geometry, a square pyramid is a Pyramid (geometry), pyramid with a square base and four triangles, having a total of five faces. If the Apex (geometry), apex of the pyramid is directly above the center of the square, it is a ''right square pyramid'' with four isosceles triangles; otherwise, it is an ''oblique square pyramid''. When all of the pyramid's edges are equal in length, its triangles are all equilateral triangle, equilateral. It is called an ''equilateral square pyramid'', an example of a Johnson solid. Square pyramids have appeared throughout the history of architecture, with examples being Egyptian pyramids and many other similar buildings. They also occur in chemistry in Square pyramidal molecular geometry, square pyramidal molecular structures. Square pyramids are often used in the construction of other polyhedra. Many mathematicians in ancient times discovered the formula for the volume of a square pyramid with different approaches. Special cases Right squar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
5-cell Boerdijk Coxeter Helix
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pentahedroid, tetrahedral pyramid, or 4-simplex (Coxeter's \alpha_4 polytope), the simplest possible convex 4-polytope, and is analogous to the tetrahedron in three dimensions and the triangle in two dimensions. The 5-cell is a 4-dimensional pyramid with a tetrahedral base and four tetrahedral sides. The regular 5-cell is bounded by five regular tetrahedra, and is one of the six regular convex 4-polytopes (the four-dimensional analogues of the Platonic solids). A regular 5-cell can be constructed from a regular tetrahedron by adding a fifth vertex one edge length distant from all the vertices of the tetrahedron. This cannot be done in 3-dimensional space. The regular 5-cell is a solution to the problem: ''Make 10 equilateral triangles, all of the same size, using ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
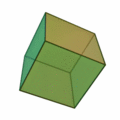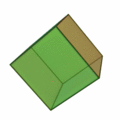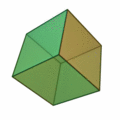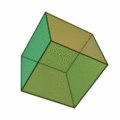
16-cell Boerdijk Coxeter Helix
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. It is also called C16, hexadecachoron, or hexdecahedroid.Matila Ghyka, ''The Geometry of Art and Life'' (1977), p.68 It is the 4-dimensional member of an infinite family of polytopes called cross-polytopes, ''orthoplexes'', or ''hyperoctahedrons'' which are analogous to the octahedron in three dimensions. It is Coxeter's \beta_4 polytope. The dual polytope is the tesseract (4-cube), which it can be combined with to form a compound figure. The cells of the 16-cell are dual to the 16 vertices of the tesseract. Geometry The 16-cell is the second in the sequence of 6 convex regular 4-polytopes (in order of size and complexity). Each of its 4 successor convex regular 4-polytopes can be constructed as the convex hull of a po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
600-cell Boerdijk Coxeter Helix
6 (six) is the natural number following 5 and preceding 7. It is a composite number and the smallest perfect number. In mathematics A six-sided polygon is a hexagon, one of the three regular polygons capable of tiling the plane. A hexagon also has 6 edges as well as 6 internal and external angles. 6 is the second smallest composite number. It is also the first number that is the sum of its proper divisors, making it the smallest perfect number. It is also the only perfect number that doesn't have a digital root of 1. 6 is the first unitary perfect number, since it is the sum of its positive proper unitary divisors, without including itself. Only five such numbers are known to exist. 6 is the largest of the four all-Harshad numbers. 6 is the 2nd superior highly composite number, the 2nd colossally abundant number, the 3rd triangular number, the 4th highly composite number, a pronic number, a congruent number, a harmonic divisor number, and a semiprime. 6 is also the first ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |