|
Birth–death Process
The birth–death process (or birth-and-death process) is a special case of continuous-time Markov process where the state transitions are of only two types: "births", which increase the state variable by one and "deaths", which decrease the state by one. It was introduced by William Feller. The model's name comes from a common application, the use of such models to represent the current size of a population where the transitions are literal births and deaths. Birth–death processes have many applications in demography, queueing theory, performance engineering, epidemiology, biology and other areas. They may be used, for example, to study the evolution of bacteria, the number of people with a disease within a population, or the number of customers in line at the supermarket. Definition When a birth occurs, the process goes from state ''n'' to ''n'' + 1. When a death occurs, the process goes from state ''n'' to state ''n'' − 1. The process is speci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous-time Markov Process
A continuous-time Markov chain (CTMC) is a continuous stochastic process in which, for each state, the process will change state according to an exponential random variable and then move to a different state as specified by the probabilities of a stochastic matrix. An equivalent formulation describes the process as changing state according to the least value of a set of exponential random variables, one for each possible state it can move to, with the parameters determined by the current state. An example of a CTMC with three states \ is as follows: the process makes a transition after the amount of time specified by the holding time—an exponential random variable E_i, where ''i'' is its current state. Each random variable is independent and such that E_0\sim \text(6), E_1\sim \text(12) and E_2\sim \text(18). When a transition is to be made, the process moves according to the jump chain, a discrete-time Markov chain with stochastic matrix: :\begin 0 & \frac & \frac \\ \frac & 0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Walk
In mathematics, a random walk, sometimes known as a drunkard's walk, is a stochastic process that describes a path that consists of a succession of random steps on some Space (mathematics), mathematical space. An elementary example of a random walk is the random walk on the integer number line \mathbb Z which starts at 0, and at each step moves +1 or −1 with equal probability. Other examples include the path traced by a molecule as it travels in a liquid or a gas (see Brownian motion), the search path of a foraging animal, or the price of a fluctuating random walk hypothesis, stock and the financial status of a gambler. Random walks have applications to engineering and many scientific fields including ecology, psychology, computer science, physics, chemistry, biology, economics, and sociology. The term ''random walk'' was first introduced by Karl Pearson in 1905. Realizations of random walks can be obtained by Monte Carlo Simulation, Monte Carlo simulation. Lattice random ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Queueing Model
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service. Queueing theory has its origins in research by Agner Krarup Erlang, who created models to describe the system of incoming calls at the Copenhagen Telephone Exchange Company. These ideas were seminal to the field of teletraffic engineering and have since seen applications in telecommunications, traffic engineering, computing, project management, and particularly industrial engineering, where they are applied in the design of factories, shops, offices, and hospitals. Spelling The spelling "queueing" over "queuing" is typically encountered in the academic research field. In fact, one of the flagship journals of the field is ''Queueing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
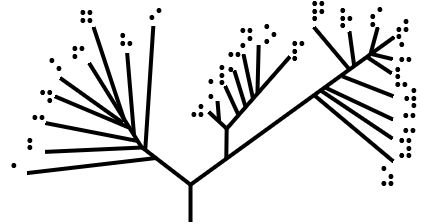
Phylogenies
A phylogenetic tree or phylogeny is a graphical representation which shows the evolutionary history between a set of species or taxa during a specific time.Felsenstein J. (2004). ''Inferring Phylogenies'' Sinauer Associates: Sunderland, MA. In other words, it is a branching diagram or a tree showing the evolutionary relationships among various biological species or other entities based upon similarities and differences in their physical or genetic characteristics. In evolutionary biology, all life on Earth is theoretically part of a single phylogenetic tree, indicating common ancestry. Phylogenetics is the study of phylogenetic trees. The main challenge is to find a phylogenetic tree representing optimal evolutionary ancestry between a set of species or taxa. Computational phylogenetics (also phylogeny inference) focuses on the algorithms involved in finding optimal phylogenetic tree in the phylogenetic landscape. Phylogenetic trees may be rooted or unrooted. In a ''rooted'' phy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phylodynamics
Viral phylodynamics is the study of how epidemiological, immunological, and evolutionary processes act and potentially interact to shape viral phylogenies. Since the term was coined in 2004, research on viral phylodynamics has focused on transmission dynamics in an effort to shed light on how these dynamics impact viral genetic variation. Transmission dynamics can be considered at the level of cells within an infected host, individual hosts within a population, or entire populations of hosts. Many viruses, especially RNA viruses, rapidly accumulate genetic variation because of short generation times and high mutation rates. Patterns of viral genetic variation are therefore heavily influenced by how quickly transmission occurs and by which entities transmit to one another. Patterns of viral genetic variation will also be affected by selection acting on viral phenotypes. Although viruses can differ with respect to many phenotypes, phylodynamic studies have to date tended to focus on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
M/M/c Model
In queueing theory, a discipline within the mathematical theory of probability, the M/M/c queue (or Erlang–C model) is a multi-server queueing model. In Kendall's notation it describes a system where arrivals form a single queue and are governed by a Poisson process, there are servers, and job service times are exponentially distributed. It is a generalisation of the M/M/1 queue which considers only a single server. The model with infinitely many servers is the M/M/∞ queue. Model definition An M/M/c queue is a stochastic process whose state space is the set where the value corresponds to the number of customers in the system, including any currently in service. * Arrivals occur at rate according to a Poisson process and move the process from state to +1. * Service times have an exponential distribution with parameter . If there are fewer than jobs, some of the servers will be idle. If there are more than jobs, the jobs queue in a buffer. * The buffer is of infinite siz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
M/M/1 Model
In queueing theory, a discipline within the mathematical theory of probability, an M/M/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times have an exponential distribution. The model name is written in Kendall's notation. The model is the most elementary of queueing models and an attractive object of study as closed-form expressions can be obtained for many metrics of interest in this model. An extension of this model with more than one server is the M/M/c queue. Model definition An M/M/1 queue is a stochastic process whose state space is the set where the value corresponds to the number of customers in the system, including any currently in service. * Arrivals occur at rate λ according to a Poisson process and move the process from state ''i'' to ''i'' + 1. * Service times have an exponential distribution with rate parameter μ in the M/M/1 queue, where 1/μ is the mean se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pure Birth Process
In probability theory, a birth process or a pure birth process is a special case of a continuous-time Markov process and a generalisation of a Poisson process. It defines a continuous process which takes values in the natural numbers and can only increase by one (a "birth") or remain unchanged. This is a type of birth–death process with no deaths. The rate at which births occur is given by an exponential random variable whose parameter depends only on the current value of the process Definition Birth rates definition A birth process with birth rates (\lambda_n, n\in \mathbb) and initial value k\in \mathbb is a minimal right-continuous process (X_t, t\ge 0) such that X_0=k and the interarrival times T_i = \inf\ - \inf\ are independent exponential random variables with parameter \lambda_i. Infinitesimal definition A birth process with rates (\lambda_n, n\in \mathbb) and initial value k\in \mathbb is a process (X_t, t\ge 0) such that: * X_0=k * \forall s,t\ge 0: s [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Population Size
In population genetics and population ecology, population size (usually denoted ''N'') is a countable quantity representing the number of individual organisms in a population. Population size is directly associated with amount of genetic drift, and is the underlying cause of effects like population bottlenecks and the founder effect. Genetic drift is the major source of decrease of genetic diversity within populations which drives fixation and can potentially lead to speciation events. Genetic drift Of the five conditions required to maintain Hardy-Weinberg Equilibrium, infinite population size will always be violated; this means that some degree of genetic drift is always occurring. Smaller population size leads to increased genetic drift, it has been hypothesized that this gives these groups an evolutionary advantage for acquisition of genome complexity. An alternate hypothesis posits that while genetic drift plays a larger role in small populations developing complexity, s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Little O Notation
Big ''O'' notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by German mathematicians Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for ''Ordnung'', meaning the order of approximation. In computer science, big O notation is used to classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetical function and a better understood approximation; one well-known example is the remainder term in the prime number theorem. Big O notation is also used in many other fields to provide similar estimates. Big O notation characterizes functions according to their growth rat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Big O Notation
Big ''O'' notation is a mathematical notation that describes the asymptotic analysis, limiting behavior of a function (mathematics), function when the Argument of a function, argument tends towards a particular value or infinity. Big O is a member of a #Related asymptotic notations, family of notations invented by German mathematicians Paul Gustav Heinrich Bachmann, Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for '':wikt:Ordnung#German, Ordnung'', meaning the order of approximation. In computer science, big O notation is used to Computational complexity theory, classify algorithms according to how their run time or space requirements grow as the input size grows. In analytic number theory, big O notation is often used to express a bound on the difference between an arithmetic function, arithmetical function and a better understood approximation; one well-known exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Difference Equations
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter k that is independent of n; this number k is called the ''order'' of the relation. If the values of the first k numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation. In ''linear recurrences'', the th term is equated to a linear function of the k previous terms. A famous example is the recurrence for the Fibonacci numbers, F_n=F_+F_ where the order k is two and the linear function merely adds the two previous terms. This example is a linear recurrence with constant coefficients, because the coefficients of the linear function (1 and 1) are constants that do not depend on n. For these recurrences, one can express the general term of the sequence as a closed-form expression o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |