|
Asymptotic Theory (statistics)
In statistics, asymptotic theory, or large sample theory, is a framework for assessing properties of estimators and statistical tests. Within this framework, it is often assumed that the sample size may grow indefinitely; the properties of estimators and tests are then evaluated under the limit of . In practice, a limit evaluation is considered to be approximately valid for large finite sample sizes too.Höpfner, R. (2014), Asymptotic Statistics, Walter de Gruyter. 286 pag. , Overview Most statistical problems begin with a dataset of size . The asymptotic theory proceeds by assuming that it is possible (in principle) to keep collecting additional data, thus that the sample size grows infinitely, i.e. . Under the assumption, many results can be obtained that are unavailable for samples of finite size. An example is the weak law of large numbers. The law states that for a sequence of independent and identically distributed (IID) random variables , if one value is drawn from each rand ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptotic Distribution
In mathematics and statistics, an asymptotic distribution is a probability distribution that is in a sense the "limiting" distribution of a sequence of distributions. One of the main uses of the idea of an asymptotic distribution is in providing approximations to the cumulative distribution functions of statistical estimators. Definition A sequence of distributions corresponds to a sequence of random variables ''Zi'' for ''i'' = 1, 2, ..., I . In the simplest case, an asymptotic distribution exists if the probability distribution of ''Zi'' converges to a probability distribution (the asymptotic distribution) as ''i'' increases: see convergence in distribution. A special case of an asymptotic distribution is when the sequence of random variables is always zero or ''Zi'' = 0 as ''i'' approaches infinity. Here the asymptotic distribution is a degenerate distribution, corresponding to the value zero. However, the most usual sense in which the term asymptotic distribution is used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exact Statistics
Exact statistics, such as that described in exact test, is a branch of statistics that was developed to provide more accurate results pertaining to statistical testing and interval estimation by eliminating procedures based on asymptotic and approximate statistical methods. The main characteristic of exact methods is that statistical tests and confidence intervals are based on exact probability statements that are valid for any sample size. Exact statistical methods help avoid some of the unreasonable assumptions of traditional statistical methods, such as the assumption of equal variances in classical ANOVA. They also allow exact inference on variance components of mixed models. When exact ''p''-values and confidence intervals are computed under a certain distribution, such as the normal distribution, then the underlying methods are referred to as exact parametric methods. The exact methods that do not make any distributional assumptions are referred to as exact nonparametric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptotic Analysis
In mathematical analysis, asymptotic analysis, also known as asymptotics, is a method of describing limiting behavior. As an illustration, suppose that we are interested in the properties of a function as becomes very large. If , then as becomes very large, the term becomes insignificant compared to . The function is said to be "''asymptotically equivalent'' to , as ". This is often written symbolically as , which is read as " is asymptotic to ". An example of an important asymptotic result is the prime number theorem. Let denote the prime-counting function (which is not directly related to the constant pi), i.e. is the number of prime numbers that are less than or equal to . Then the theorem states that \pi(x)\sim\frac. Asymptotic analysis is commonly used in computer science as part of the analysis of algorithms and is often expressed there in terms of big O notation. Definition Formally, given functions and , we define a binary relation f(x) \sim g(x) \q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Delta Method
In statistics, the delta method is a result concerning the approximate probability distribution for a function of an asymptotically normal statistical estimator from knowledge of the limiting variance of that estimator. History The delta method was derived from propagation of error, and the idea behind was known in the early 19th century. Its statistical application can be traced as far back as 1928 by T. L. Kelley. A formal description of the method was presented by J. L. Doob in 1935. Robert Dorfman also described a version of it in 1938. Univariate delta method While the delta method generalizes easily to a multivariate setting, careful motivation of the technique is more easily demonstrated in univariate terms. Roughly, if there is a sequence of random variables satisfying :, where ''θ'' and ''σ''2 are finite valued constants and \xrightarrow denotes convergence in distribution, then : for any function ''g'' satisfying the property that exists and is non-zero v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Slutsky's Theorem
In probability theory, Slutsky’s theorem extends some properties of algebraic operations on convergent sequences of real numbers to sequences of random variables. The theorem was named after Eugen Slutsky. Slutsky's theorem is also attributed to Harald Cramér. Statement Let X_n, Y_n be sequences of scalar/vector/matrix random elements. If X_n converges in distribution to a random element X and Y_n converges in probability to a constant c, then * X_n + Y_n \ \xrightarrow\ X + c ; * X_nY_n \ \xrightarrow\ Xc ; * X_n/Y_n \ \xrightarrow\ X/c, provided that ''c'' is invertible, where \xrightarrow denotes convergence in distribution. Notes: # The requirement that ''Yn'' converges to a constant is important — if it were to converge to a non-degenerate random variable, the theorem would be no longer valid. For example, let X_n \sim (0,1) and Y_n = -X_n. The sum X_n + Y_n = 0 for all values of ''n''. Moreover, Y_n \, \xrightarrow \, (-1,0), but X_n + Y_n does not converge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
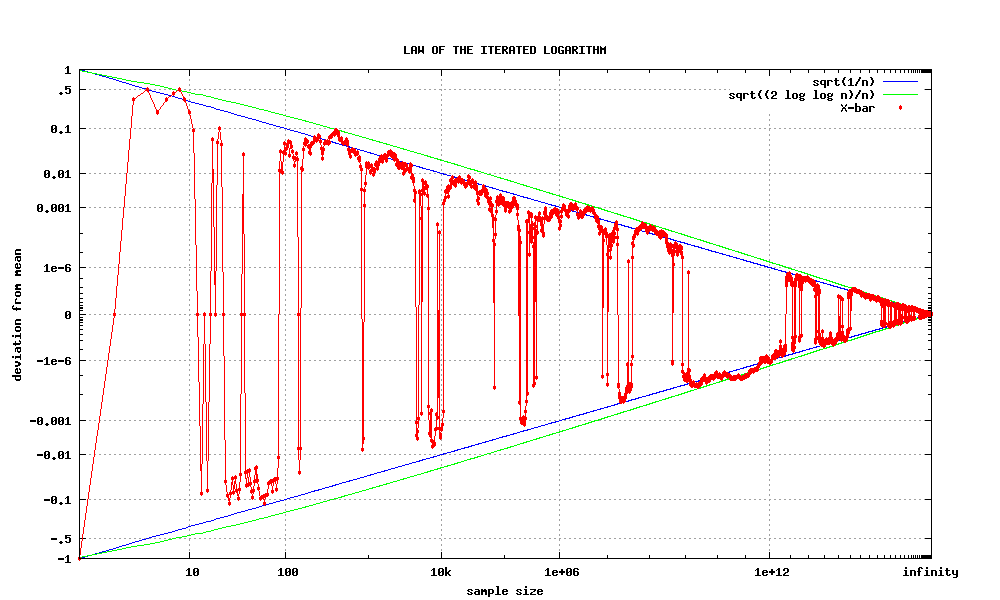
Law Of The Iterated Logarithm
In probability theory, the law of the iterated logarithm describes the magnitude of the fluctuations of a random walk. The original statement of the law of the iterated logarithm is due to A. Ya. Khinchin (1924). Another statement was given by A. N. Kolmogorov in 1929. Statement Let be independent, identically distributed random variables with means zero and unit variances. Let ''S''''n'' = ''Y''1 + ... + ''Y''''n''. Then : \limsup_ \frac = 1 \quad \text, where “log” is the natural logarithm, “lim sup” denotes the limit superior, and “a.s.” stands for “almost surely”. Discussion The law of iterated logarithms operates “in between” the law of large numbers and the central limit theorem. There are two versions of the law of large numbers — the weak and the strong — and they both state that the sums ''S''''n'', scaled by ''n''−1, converge to zero, respectively in probability and almost surely: : \frac \ \xrightarrow\ 0, \qquad \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Large Numbers
In probability theory, the law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value and tends to become closer to the expected value as more trials are performed. The LLN is important because it guarantees stable long-term results for the averages of some random events. For example, while a casino may lose money in a single spin of the roulette wheel, its earnings will tend towards a predictable percentage over a large number of spins. Any winning streak by a player will eventually be overcome by the parameters of the game. Importantly, the law applies (as the name indicates) only when a ''large number'' of observations are considered. There is no principle that a small number of observations will coincide with the expected value or that a streak of one value will immediately be "balance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glivenko–Cantelli Theorem
In the theory of probability, the Glivenko–Cantelli theorem (sometimes referred to as the Fundamental Theorem of Statistics), named after Valery Ivanovich Glivenko and Francesco Paolo Cantelli, determines the asymptotic behaviour of the empirical distribution function as the number of independent and identically distributed observations grows. The uniform convergence of more general empirical measures becomes an important property of the Glivenko–Cantelli classes of functions or sets. The Glivenko–Cantelli classes arise in Vapnik–Chervonenkis theory, with applications to machine learning. Applications can be found in econometrics making use of M-estimators. Statement Assume that X_1,X_2,\dots are independent and identically distributed random variables in \mathbb with common cumulative distribution function F(x). The '' empirical distribution function'' for X_1,\dots,X_n is defined by :F_n(x)=\frac\sum_^n I_(x) = \frac\left, \left\\ where I_C is the indicator f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Mapping Theorem
In probability theory, the continuous mapping theorem states that continuous functions preserve limits even if their arguments are sequences of random variables. A continuous function, in Heine’s definition, is such a function that maps convergent sequences into convergent sequences: if ''xn'' → ''x'' then ''g''(''xn'') → ''g''(''x''). The ''continuous mapping theorem'' states that this will also be true if we replace the deterministic sequence with a sequence of random variables , and replace the standard notion of convergence of real numbers “→” with one of the types of convergence of random variables. This theorem was first proved by Henry Mann and Abraham Wald in 1943, and it is therefore sometimes called the Mann–Wald theorem. Meanwhile, Denis Sargan refers to it as the general transformation theorem. Statement Let , ''X'' be random elements defined on a metric space ''S''. Suppose a function (where ''S′'' is another metric space) has the set of disconti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Central Limit Theorem
In probability theory, the central limit theorem (CLT) establishes that, in many situations, when independent random variables are summed up, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions. This theorem has seen many changes during the formal development of probability theory. Previous versions of the theorem date back to 1811, but in its modern general form, this fundamental result in probability theory was precisely stated as late as 1920, thereby serving as a bridge between classical and modern probability theory. If X_1, X_2, \dots, X_n, \dots are random samples drawn from a population with overall mean \mu and finite variance and if \bar_n is the sample mean of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confidence Region
In statistics, a confidence region is a multi-dimensional generalization of a confidence interval. It is a set of points in an ''n''-dimensional space, often represented as an ellipsoid around a point which is an estimated solution to a problem, although other shapes can occur. Interpretation The confidence region is calculated in such a way that if a set of measurements were repeated many times and a confidence region calculated in the same way on each set of measurements, then a certain percentage of the time (e.g. 95%) the confidence region would include the point representing the "true" values of the set of variables being estimated. However, unless certain assumptions about prior probabilities are made, it does not mean, when one confidence region has been calculated, that there is a 95% probability that the "true" values lie inside the region, since we do not assume any particular probability distribution of the "true" values and we may or may not have other information a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |