|
A. F. Théry
A is the first letter of the Latin and English alphabet. A may also refer to: Science and technology Quantities and units * ''a'', a measure for the attraction between particles in the Van der Waals equation * ''A'' value, a measure of substituent effects on the stereochemistry of cyclohexane * absorbance (''A'') * acceleration (''a'') * activity (chemistry) (''a'') * adsorption (a) * annum (a), for year * are (a), a unit of area (equal to 100 square metres; redirects to ''hectare'') * atto- (a-), the SI prefix meaning 10−18 * Ampere (A), unit of electric current * ångström (Å) a unit of length (equal to 1 metres) * area (''A'') * attenuation coefficient (''a'') * Bohr radius (''a''0) * chemical affinity (''A'') * gain (electronics) (''A'') * Hall coefficient (''A''H) * Hamaker constant (''A'') * Helmholtz free energy (''A'') * Hyperfine coupling constant (''a'' or ''A'') * magnetic vector potential (''A'') * mass number of a nuclide (''A'') * pre-exponential fact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hall Coefficient
The Hall effect is the production of a potential difference (the Hall voltage) across an electrical conductor that is transverse to an electric current in the conductor and to an applied magnetic field perpendicular to the current. It was discovered by Edwin Hall in 1879. The ''Hall coefficient'' is defined as the ratio of the induced electric field to the product of the current density and the applied magnetic field. It is a characteristic of the material from which the conductor is made, since its value depends on the type, number, and properties of the charge carriers that constitute the current. Discovery Wires carrying current in a magnetic field experience a mechanical force perpendicular to both the current and magnetic field. In the 1820s, André-Marie Ampère observed this underlying mechanism that led to the discovery of the Hall effect. However it was not until a solid mathematical basis for electromagnetism was systematized by James Clerk Maxwell's " On P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
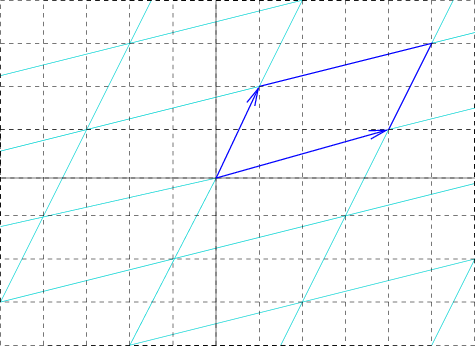
Unit Cell Length
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector, for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogram or parallelepiped) that generates the whole tiling using only translations. There are two special cases of the unit cell: the primitive cell and the conventional cell. The primitive cell is a unit cell corresponding to a single lattice point, it is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermal Diffusivity
In thermodynamics, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It is a measure of the rate of heat transfer inside a material and has SI, SI units of m2/s. It is an intensive property. Thermal diffusivity is usually denoted by lowercase alpha (), but , , (kappa), , , D_T are also used. The formula is \alpha = \frac, where : is thermal conductivity (W/(m·K)), : is specific heat capacity (J/(kg·K)), : is density (kg/m3). Together, can be considered the volumetric heat capacity (J/(m3·K)). Thermal diffusivity is a positive coefficient in the heat equation: \frac = \alpha \nabla^2 T. One way to view thermal diffusivity is as the ratio of the time derivative of temperature to its Second derivative#Generalization to higher dimensions, curvature, quantifying the rate at which temperature concavity is "smoothed out". In a substance with high thermal diffusivity, heat moves rapidly through it because the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Surface Area
Specific surface area (SSA) is a property of solids defined as the total surface area (SA) of a material per unit mass, (with units of m2/kg or m2/g). Alternatively, it may be defined as SA per solid or bulk volume (units of m2/m3 or m−1). It is a physical value that can be used to determine the type and properties of a material (e.g. soil or snow). It has a particular importance for adsorption, heterogeneous catalysis, and reactions on surfaces. Measurement Values obtained for specific surface area depend on the method of measurement. In adsorption based methods, the size of the adsorbate molecule (the probe molecule), the exposed crystallographic planes at the surface and measurement temperature all affect the obtained specific surface area. For this reason, in addition to the most commonly used Brunauer–Emmett–Teller (N2-BET) adsorption method, several techniques have been developed to measure the specific surface area of particulate materials at ambient tempera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotational Constant
In rotordynamics, the rigid rotor is a mechanical model of rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space requires three angles, known as Euler angles. A special rigid rotor is the ''linear rotor'' requiring only two angles to describe, for example of a diatomic molecule. More general molecules are 3-dimensional, such as water (asymmetric rotor), ammonia (symmetric rotor), or methane (spherical rotor). Linear rotor The linear rigid rotor model consists of two point masses located at fixed distances from their center of mass. The fixed distance between the two masses and the values of the masses are the only characteristics of the rigid model. However, for many actual diatomics this model is too restrictive since distances are usually not completely fixed. Corrections on the rigid model can be made to compensate for small variations in the distance. Even in such a case the rigid rotor model is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |