|
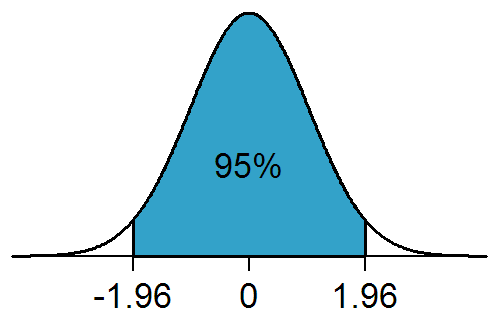
1.96
In probability and statistics, the 97.5th percentile point of the standard normal distribution is a number commonly used for statistical calculations. The approximate value of this number is 1.96, meaning that 95% of the area under a normal curve lies within approximately 1.96 standard deviations of the mean. Because of the central limit theorem, this number is used in the construction of approximate 95% confidence intervals. Its ubiquity is due to the arbitrary but common convention of using confidence intervals with 95% probability in science and frequentist statistics, though other probabilities (90%, 99%, etc.) are sometimes used. This convention seems particularly common in medical statistics, but is also common in other areas of application, such as earth sciences, social sciences and business research. There is no single accepted name for this number; it is also commonly referred to as the "standard normal deviate", " normal score" or " Z score" for the 97. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probit
In probability theory and statistics, the probit function is the quantile function associated with the standard normal distribution. It has applications in data analysis and machine learning, in particular exploratory statistical graphics and specialized regression modeling of binary response variables. Mathematically, the probit is the inverse of the cumulative distribution function of the standard normal distribution, which is denoted as \Phi(z), so the probit is defined as :\operatorname(p) = \Phi^(p) \quad \text \quad p \in (0,1). Largely because of the central limit theorem, the standard normal distribution plays a fundamental role in probability theory and statistics. If we consider the familiar fact that the standard normal distribution places 95% of probability between −1.96 and 1.96, and is symmetric around zero, it follows that :\Phi(-1.96) = 0.025 = 1-\Phi(1.96).\,\! The probit function gives the 'inverse' computation, generating a value of a standard normal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Margin Of Error
The margin of error is a statistic expressing the amount of random sampling error in the results of a survey. The larger the margin of error, the less confidence one should have that a poll result would reflect the result of a census of the entire population. The margin of error will be positive whenever a population is incompletely sampled and the outcome measure has positive variance, which is to say, the measure ''varies''. The term ''margin of error'' is often used in non-survey contexts to indicate observational error in reporting measured quantities. Concept Consider a simple ''yes/no'' poll P as a sample of n respondents drawn from a population N \text(n \ll N) reporting the percentage p of ''yes'' responses. We would like to know how close p is to the true result of a survey of the entire population N, without having to conduct one. If, hypothetically, we were to conduct poll P over subsequent samples of n respondents (newly drawn from N), we would expect those su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reference Range
In medicine and health-related fields, a reference range or reference interval is the range or the interval of values that is deemed normal for a physiological measurement in healthy persons (for example, the amount of creatinine in the blood, or the partial pressure of oxygen). It is a basis for comparison for a physician or other health professional to interpret a set of test results for a particular patient. Some important reference ranges in medicine are reference ranges for blood tests and reference ranges for urine tests. The standard definition of a reference range (usually referred to if not otherwise specified) originates in what is most prevalent in a reference group taken from the general (i.e. total) population. This is the general reference range. However, there are also ''optimal health ranges'' (ranges that appear to have the optimal health impact) and ranges for particular conditions or statuses (such as pregnancy reference ranges for hormone levels). Val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Error (statistics)
The standard error (SE) of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean (SEM). The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. This forms a distribution of different means, and this distribution has its own mean and variance. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely around the population mean. Therefore, the relationship between the standard error of the mean and the standard deviation is such that, for a given sample size, the standard error of the mean equals the standard deviation divided by the square root of the sample siz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Curve
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal distribu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ronald Fisher
Sir Ronald Aylmer Fisher (17 February 1890 – 29 July 1962) was a British polymath who was active as a mathematician, statistician, biologist, geneticist, and academic. For his work in statistics, he has been described as "a genius who almost single-handedly created the foundations for modern statistical science" and "the single most important figure in 20th century statistics". In genetics, his work used mathematics to combine Mendelian genetics and natural selection; this contributed to the revival of Darwinism in the early 20th-century revision of the theory of evolution known as the modern synthesis. For his contributions to biology, Fisher has been called "the greatest of Darwin’s successors". Fisher held strong views on race and eugenics, insisting on racial differences. Although he was clearly a eugenist and advocated for the legalization of voluntary sterilization of those with heritable mental disabilities, there is some debate as to whether Fisher support ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decimal Places
Significant figures (also known as the significant digits, ''precision'' or ''resolution'') of a number in positional notation are digits in the number that are reliable and necessary to indicate the quantity of something. If a number expressing the result of a measurement (e.g., length, pressure, volume, or mass) has more digits than the number of digits allowed by the measurement resolution, then only as many digits as allowed by the measurement resolution are reliable, and so only these can be significant figures. For example, if a length measurement gives 114.8 mm while the smallest interval between marks on the ruler used in the measurement is 1 mm, then the first three digits (1, 1, and 4, showing 114 mm) are certain and so they are significant figures. Digits which are uncertain but ''reliable'' are also considered significant figures. In this example, the last digit (8, which adds 0.8 mm) is also considered a significant figure even though the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confidence Interval
In frequentist statistics, a confidence interval (CI) is a range of estimates for an unknown parameter. A confidence interval is computed at a designated ''confidence level''; the 95% confidence level is most common, but other levels, such as 90% or 99%, are sometimes used. The confidence level represents the long-run proportion of corresponding CIs that contain the true value of the parameter. For example, out of all intervals computed at the 95% level, 95% of them should contain the parameter's true value. Factors affecting the width of the CI include the sample size, the variability in the sample, and the confidence level. All else being the same, a larger sample produces a narrower confidence interval, greater variability in the sample produces a wider confidence interval, and a higher confidence level produces a wider confidence interval. Definition Let be a random sample from a probability distribution with statistical parameter , which is a quantity to be esti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Python (programming Language)
Python is a high-level, general-purpose programming language. Its design philosophy emphasizes code readability with the use of significant indentation. Python is dynamically-typed and garbage-collected. It supports multiple programming paradigms, including structured (particularly procedural), object-oriented and functional programming. It is often described as a "batteries included" language due to its comprehensive standard library. Guido van Rossum began working on Python in the late 1980s as a successor to the ABC programming language and first released it in 1991 as Python 0.9.0. Python 2.0 was released in 2000 and introduced new features such as list comprehensions, cycle-detecting garbage collection, reference counting, and Unicode support. Python 3.0, released in 2008, was a major revision that is not completely backward-compatible with earlier versions. Python 2 was discontinued with version 2.7.18 in 2020. Python consistently ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. Standard deviation may be abbreviated SD, and is most commonly represented in mathematical texts and equations by the lower case Greek letter σ (sigma), for the population standard deviation, or the Latin letter '' s'', for the sample standard deviation. The standard deviation of a random variable, sample, statistical population, data set, or probability distribution is the square root of its variance. It is algebraically simpler, though in practice less robust, than the average absolute deviation. A useful property of the standard deviation is that, unlike the variance, it is expressed in the same unit as the data. The standard deviation o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |