Surface vertex on:
[Wikipedia]
[Google]
[Amazon]
In
 The cardinal points lie on the
The cardinal points lie on the
 The front and rear (or back) focal planes are defined as the planes, perpendicular to the optic axis, which pass through the front and rear focal points. An object infinitely far from the optical system forms an
The front and rear (or back) focal planes are defined as the planes, perpendicular to the optic axis, which pass through the front and rear focal points. An object infinitely far from the optical system forms an  A diaphragm or "stop" at the rear focal plane of a lens can be used to filter rays by angle, since an aperture centred on the optical axis there will only pass rays that were emitted from the object at a sufficiently small angle from the optical axis. Using a sufficiently small aperture in the rear focal plane will make the lens object-space telecentric.
Similarly, the allowed range of angles on the output side of the lens can be filtered by putting an aperture at the front focal plane of the lens (or a lens group within the overall lens), and a sufficiently small aperture will make the lens image-space telecentric. This is important for DSLR cameras having CCD sensors. The pixels in these sensors are more sensitive to rays that hit them straight on than to those that strike at an angle. A lens that does not control the angle of incidence at the detector will produce pixel vignetting in the images.
A diaphragm or "stop" at the rear focal plane of a lens can be used to filter rays by angle, since an aperture centred on the optical axis there will only pass rays that were emitted from the object at a sufficiently small angle from the optical axis. Using a sufficiently small aperture in the rear focal plane will make the lens object-space telecentric.
Similarly, the allowed range of angles on the output side of the lens can be filtered by putting an aperture at the front focal plane of the lens (or a lens group within the overall lens), and a sufficiently small aperture will make the lens image-space telecentric. This is important for DSLR cameras having CCD sensors. The pixels in these sensors are more sensitive to rays that hit them straight on than to those that strike at an angle. A lens that does not control the angle of incidence at the detector will produce pixel vignetting in the images.
 The front and rear nodal points of a lens have the property that a ray aimed at one of them will be refracted by the lens such that it appears to have come from the other with the same angle to the optical axis. (Angular magnification between nodal points is +1.) The nodal points therefore do for angles what the principal planes do for transverse distance. If the medium on both sides of an optical system is the same (e.g., air or vacuum), then the front and rear nodal points coincide with the front and rear principal points, respectively.
Gauss's original 1841 paper only discussed the main rays through the focal points. A colleague, Johann Listing, was the first to describe the nodal points in 1845 to evaluate the human eye, where the image is in fluid. The cardinal points were all included in a single diagram as early as 1864 (Donders), with the object in air and the image in a different medium.
The front and rear nodal points of a lens have the property that a ray aimed at one of them will be refracted by the lens such that it appears to have come from the other with the same angle to the optical axis. (Angular magnification between nodal points is +1.) The nodal points therefore do for angles what the principal planes do for transverse distance. If the medium on both sides of an optical system is the same (e.g., air or vacuum), then the front and rear nodal points coincide with the front and rear principal points, respectively.
Gauss's original 1841 paper only discussed the main rays through the focal points. A colleague, Johann Listing, was the first to describe the nodal points in 1845 to evaluate the human eye, where the image is in fluid. The cardinal points were all included in a single diagram as early as 1864 (Donders), with the object in air and the image in a different medium.
 The nodal points characterize a ray that goes through the centre of a lens without any angular deviation. For a lens in air with the aperture stop at the principal planes, this would be a chief ray since the nodal points and principal points coincide in this case. This is a valuable addition in its own right to what has come to be called "Gaussian optics", and if the image was in fluid instead, then that same ray would refract into the new medium, as it does in the diagram to the right. A ray through the nodal points has parallel input and output portions (blue). A simple method to find the rear nodal point for a lens with air on one side and fluid on the other is to take the rear focal length and divide it by the image medium index, which gives the effective focal length (EFL) of the lens. The EFL is the distance from the rear nodal point to the rear focal point.
The power of a lens is equal to or . For collimated light, a lens could be placed in air at the second nodal point of an optical system to give the same paraxial properties as an original lens system with an image in fluid. The power of the entire eye is about 60 dioptres, for example. Similarly, a lens used totally in fluid, like an
The nodal points characterize a ray that goes through the centre of a lens without any angular deviation. For a lens in air with the aperture stop at the principal planes, this would be a chief ray since the nodal points and principal points coincide in this case. This is a valuable addition in its own right to what has come to be called "Gaussian optics", and if the image was in fluid instead, then that same ray would refract into the new medium, as it does in the diagram to the right. A ray through the nodal points has parallel input and output portions (blue). A simple method to find the rear nodal point for a lens with air on one side and fluid on the other is to take the rear focal length and divide it by the image medium index, which gives the effective focal length (EFL) of the lens. The EFL is the distance from the rear nodal point to the rear focal point.
The power of a lens is equal to or . For collimated light, a lens could be placed in air at the second nodal point of an optical system to give the same paraxial properties as an original lens system with an image in fluid. The power of the entire eye is about 60 dioptres, for example. Similarly, a lens used totally in fluid, like an
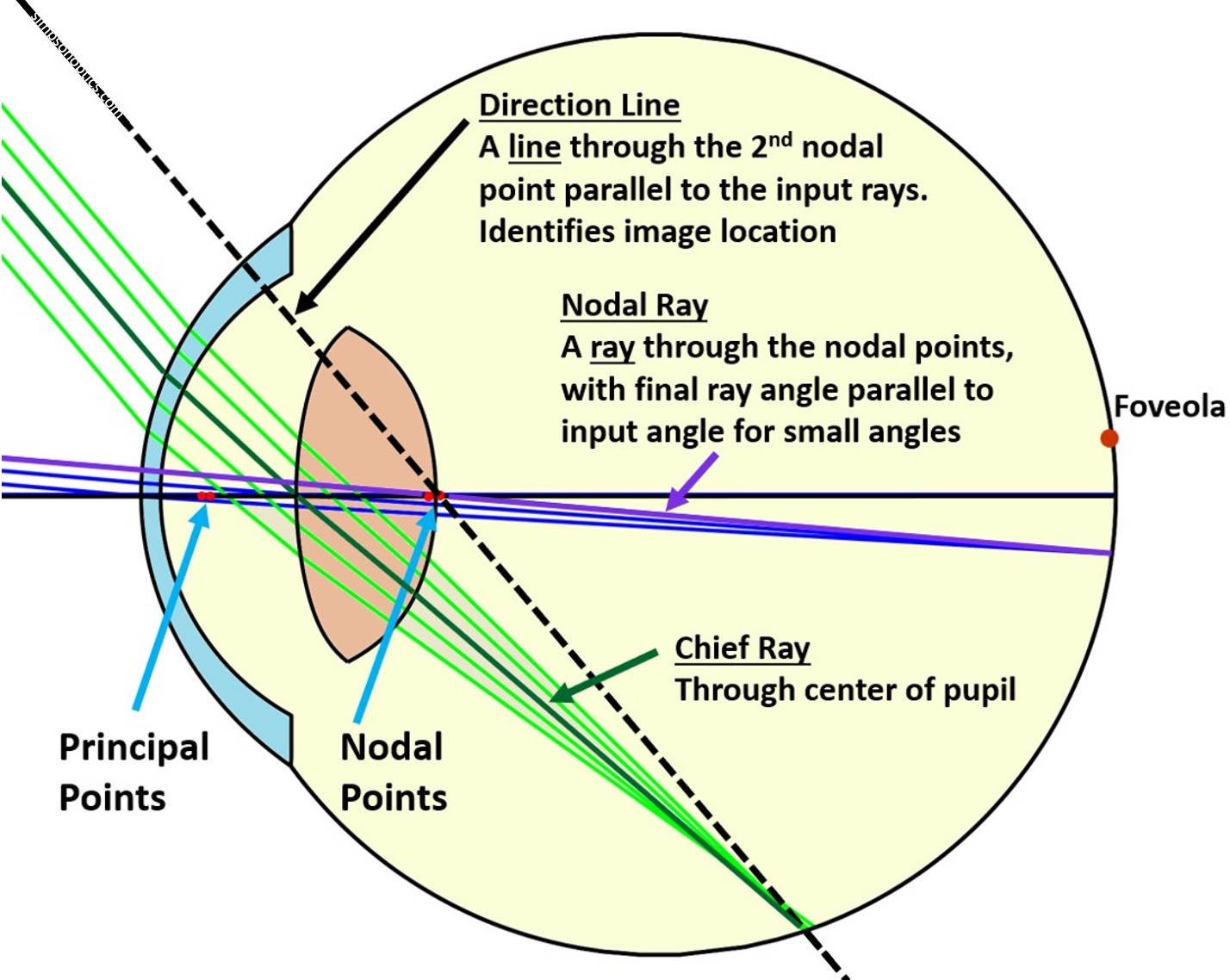 The eye itself has a second special use of the nodal point that tends to be obscured by paraxial discussions. The cornea and retina are highly curved, unlike most imaging systems, and the optical design of the eye has the property that a "direction line" that is parallel to the input rays can be used to find the magnification or to scale retinal locations. This line passes approximately through the 2nd nodal point, but rather than being an actual paraxial ray, it identifies the image formed by ray bundles that pass through the centre of the pupil. The terminology comes from Volkmann in 1836, but most discussions incorrectly imply that paraxial properties of rays extend to very large angles, rather than recognizing this as a unique property of the eye's design. This scaling property is well-known, very useful, and very simple: angles drawn with a ruler centred on the posterior pole of the lens on a cross-section of the eye can approximately scale the retina over more than an entire hemisphere. It is only in the 2000s that the limitations of this approximation have become apparent, with an exploration into why some intraocular lens (IOL) patients see dark shadows in the far periphery (negative dysphotopsia, which is probably due to the IOL being much smaller than the natural lens.)
The eye itself has a second special use of the nodal point that tends to be obscured by paraxial discussions. The cornea and retina are highly curved, unlike most imaging systems, and the optical design of the eye has the property that a "direction line" that is parallel to the input rays can be used to find the magnification or to scale retinal locations. This line passes approximately through the 2nd nodal point, but rather than being an actual paraxial ray, it identifies the image formed by ray bundles that pass through the centre of the pupil. The terminology comes from Volkmann in 1836, but most discussions incorrectly imply that paraxial properties of rays extend to very large angles, rather than recognizing this as a unique property of the eye's design. This scaling property is well-known, very useful, and very simple: angles drawn with a ruler centred on the posterior pole of the lens on a cross-section of the eye can approximately scale the retina over more than an entire hemisphere. It is only in the 2000s that the limitations of this approximation have become apparent, with an exploration into why some intraocular lens (IOL) patients see dark shadows in the far periphery (negative dysphotopsia, which is probably due to the IOL being much smaller than the natural lens.)
Gaussian optics
Gaussian optics is a technique in geometrical optics that describes the behaviour of light rays in optical systems by using the paraxial approximation, in which only rays which make small angles with the optical axis of the system are considered. ...
, the cardinal points consist of three pairs of points located on the optical axis
An optical axis is an imaginary line that passes through the geometrical center of an optical system such as a camera lens, microscope or telescopic sight. Lens elements often have rotational symmetry about the axis.
The optical axis defines ...
of a rotationally symmetric, focal, optical system. These are the '' focal points'', the principal points, and the nodal points; there are two of each. For ''ideal'' systems, the basic imaging properties such as image size, location, and orientation are completely determined by the locations of the cardinal points. For simple cases where the medium on both sides of an optical system is air or vacuum four cardinal points are sufficient: the two focal points and either the principal points or the nodal points. The only ideal system that has been achieved in practice is a plane mirror, however the cardinal points are widely used to the behavior of real optical systems. Cardinal points provide a way to analytically simplify an optical system with many components, allowing the imaging characteristics of the system to be approximately determined with simple calculations.
Explanation
optical axis
An optical axis is an imaginary line that passes through the geometrical center of an optical system such as a camera lens, microscope or telescopic sight. Lens elements often have rotational symmetry about the axis.
The optical axis defines ...
of an optical system. Each point is defined by the effect the optical system has on rays that pass through that point, in the paraxial approximation. The paraxial approximation assumes that rays travel at shallow angles with respect to the optical axis, so that and Aperture effects are ignored: rays that do not pass through the aperture stop of the system are not considered in the discussion below.
Focal points and planes
The front ''focal point'' of an optical system, by definition, has the property that any ray that passes through it will emerge from the system parallel to theoptical axis
An optical axis is an imaginary line that passes through the geometrical center of an optical system such as a camera lens, microscope or telescopic sight. Lens elements often have rotational symmetry about the axis.
The optical axis defines ...
. The rear (or back) focal point of the system has the reverse property: rays that enter the system parallel to the optical axis are focused such that they pass through the rear focal point.
image
An image or picture is a visual representation. An image can be Two-dimensional space, two-dimensional, such as a drawing, painting, or photograph, or Three-dimensional space, three-dimensional, such as a carving or sculpture. Images may be di ...
at the rear focal plane. For an object at a finite distance, the image is formed at a different location, but rays that leave the object parallel to one another cross at the rear focal plane.
Principal planes and points
The two principal planes of a lens have the property that a ray emerging from the lens to have crossed the rear principal plane at the same distance from the optical axis that the ray to have crossed the front principal plane, as viewed from the front of the lens. This means that the lens can be treated as if all of the refraction happened at the principal planes, and rays travel parallel to the optical axis between the planes. (Linear magnification between the principal planes is +1.) The principal planes are crucial in defining the properties of an optical system, since themagnification
Magnification is the process of enlarging the apparent size, not physical size, of something. This enlargement is quantified by a size ratio called optical magnification. When this number is less than one, it refers to a reduction in size, so ...
of the system is determined by the distance from an object to the front principal plane and the distance from the rear principal plane to the object's image. The ''principal points'' are the points where the principal planes cross the optical axis.
If the medium surrounding an optical system has a refractive index
In optics, the refractive index (or refraction index) of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refrac ...
of 1 (e.g., air
An atmosphere () is a layer of gases that envelop an astronomical object, held in place by the gravity of the object. A planet retains an atmosphere when the gravity is great and the temperature of the atmosphere is low. A stellar atmosph ...
or vacuum
A vacuum (: vacuums or vacua) is space devoid of matter. The word is derived from the Latin adjective (neuter ) meaning "vacant" or "void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressur ...
), then the distance from each principal plane to the corresponding focal point is just the focal length
The focal length of an Optics, optical system is a measure of how strongly the system converges or diverges light; it is the Multiplicative inverse, inverse of the system's optical power. A positive focal length indicates that a system Converge ...
of the system. In the more general case, the distance to the foci is the focal length multiplied by the index of refraction of the medium.
For a single lens surrounded by a medium of refractive index , the locations of the principal points and with respect to the respective lens vertices are given by the formulas where is the focal length of the lens, is its thickness, and and are the radii of curvature of its surfaces. Positive signs indicate distances to the right of the corresponding vertex, and negative to the left.
For a thin lens in air, the principal planes both lie at the location of the lens. The point where they cross the optical axis is sometimes misleadingly called the optical centre of the lens. For a real lens the principal planes do not necessarily pass through the centre of the lens and can even be outside the lens.
Nodal points
 The nodal points characterize a ray that goes through the centre of a lens without any angular deviation. For a lens in air with the aperture stop at the principal planes, this would be a chief ray since the nodal points and principal points coincide in this case. This is a valuable addition in its own right to what has come to be called "Gaussian optics", and if the image was in fluid instead, then that same ray would refract into the new medium, as it does in the diagram to the right. A ray through the nodal points has parallel input and output portions (blue). A simple method to find the rear nodal point for a lens with air on one side and fluid on the other is to take the rear focal length and divide it by the image medium index, which gives the effective focal length (EFL) of the lens. The EFL is the distance from the rear nodal point to the rear focal point.
The power of a lens is equal to or . For collimated light, a lens could be placed in air at the second nodal point of an optical system to give the same paraxial properties as an original lens system with an image in fluid. The power of the entire eye is about 60 dioptres, for example. Similarly, a lens used totally in fluid, like an
The nodal points characterize a ray that goes through the centre of a lens without any angular deviation. For a lens in air with the aperture stop at the principal planes, this would be a chief ray since the nodal points and principal points coincide in this case. This is a valuable addition in its own right to what has come to be called "Gaussian optics", and if the image was in fluid instead, then that same ray would refract into the new medium, as it does in the diagram to the right. A ray through the nodal points has parallel input and output portions (blue). A simple method to find the rear nodal point for a lens with air on one side and fluid on the other is to take the rear focal length and divide it by the image medium index, which gives the effective focal length (EFL) of the lens. The EFL is the distance from the rear nodal point to the rear focal point.
The power of a lens is equal to or . For collimated light, a lens could be placed in air at the second nodal point of an optical system to give the same paraxial properties as an original lens system with an image in fluid. The power of the entire eye is about 60 dioptres, for example. Similarly, a lens used totally in fluid, like an intraocular lens
An intraocular lens (IOL) is a lens (optics), lens implanted in the human eye, eye usually as part of a treatment for cataracts or for correcting other vision problems such as myopia, near-sightedness (myopia) and farsightedness, far-sightednes ...
, has the same definition for power, with an average value of about 21 dioptres.
Nodal points and the eye
 The eye itself has a second special use of the nodal point that tends to be obscured by paraxial discussions. The cornea and retina are highly curved, unlike most imaging systems, and the optical design of the eye has the property that a "direction line" that is parallel to the input rays can be used to find the magnification or to scale retinal locations. This line passes approximately through the 2nd nodal point, but rather than being an actual paraxial ray, it identifies the image formed by ray bundles that pass through the centre of the pupil. The terminology comes from Volkmann in 1836, but most discussions incorrectly imply that paraxial properties of rays extend to very large angles, rather than recognizing this as a unique property of the eye's design. This scaling property is well-known, very useful, and very simple: angles drawn with a ruler centred on the posterior pole of the lens on a cross-section of the eye can approximately scale the retina over more than an entire hemisphere. It is only in the 2000s that the limitations of this approximation have become apparent, with an exploration into why some intraocular lens (IOL) patients see dark shadows in the far periphery (negative dysphotopsia, which is probably due to the IOL being much smaller than the natural lens.)
The eye itself has a second special use of the nodal point that tends to be obscured by paraxial discussions. The cornea and retina are highly curved, unlike most imaging systems, and the optical design of the eye has the property that a "direction line" that is parallel to the input rays can be used to find the magnification or to scale retinal locations. This line passes approximately through the 2nd nodal point, but rather than being an actual paraxial ray, it identifies the image formed by ray bundles that pass through the centre of the pupil. The terminology comes from Volkmann in 1836, but most discussions incorrectly imply that paraxial properties of rays extend to very large angles, rather than recognizing this as a unique property of the eye's design. This scaling property is well-known, very useful, and very simple: angles drawn with a ruler centred on the posterior pole of the lens on a cross-section of the eye can approximately scale the retina over more than an entire hemisphere. It is only in the 2000s that the limitations of this approximation have become apparent, with an exploration into why some intraocular lens (IOL) patients see dark shadows in the far periphery (negative dysphotopsia, which is probably due to the IOL being much smaller than the natural lens.)
Optical center
The optical center of a spherical lens is a point such that if a ray passes through it, the ray's path after leaving the lens will be parallel to its path before it entered. In the figure at right, the points ''A'' and ''B'' are where parallel lines of radii of curvature ''R''1 and ''R''2 meet the lens surfaces. As a result, dashed lines tangent to the surfaces at ''A'' and ''B'' are also parallel. Because two triangles ''OBC''2 and ''OAC''1 are similar (i.e., their angles are same), . In whatever choice of ''A'' and ''B'', the radii of curvatures and are same and the curvature center locations and are also same. As a result, the optical center location ''O'', defined by the ratio on the optical axis, is fixed for a given lens.Photography
The nodal points are widely misunderstood inphotography
Photography is the visual arts, art, application, and practice of creating images by recording light, either electronically by means of an image sensor, or chemically by means of a light-sensitive material such as photographic film. It is empl ...
, where it is commonly asserted that the light rays "intersect" at "the nodal point", that the iris diaphragm of the lens is located there, and that this is the correct pivot point for panoramic photography
Panoramic photography is a technique of photography, using specialized equipment or software, that captures images with horizontally elongated field of view, fields of view. It is sometimes known as ''wide format photography''. The term has also ...
, so as to avoid parallax
Parallax is a displacement or difference in the apparent position of an object viewed along two different sightline, lines of sight and is measured by the angle or half-angle of inclination between those two lines. Due to perspective (graphica ...
error. These claims generally arise from confusion about the optics of camera lenses, as well as confusion between the nodal points and the other cardinal points of the system. A better choice of the point about which to pivot a camera for panoramic photography can be shown to be the centre of the system's entrance pupil. Item #6. On the other hand, swing-lens cameras with fixed film position rotate the lens about the rear nodal point to stabilize the image on the film.
Surface vertices
In optics, surface vertices are the points where each optical surface crosses the optical axis. They are important primarily because they are physically measurable parameters for the optical element positions, and so the positions of the cardinal points of the optical system must be known with respect to the surface vertices to describe the system. Inanatomy
Anatomy () is the branch of morphology concerned with the study of the internal structure of organisms and their parts. Anatomy is a branch of natural science that deals with the structural organization of living things. It is an old scien ...
, the surface vertices of the eye's lens
A lens is a transmissive optical device that focuses or disperses a light beam by means of refraction. A simple lens consists of a single piece of transparent material, while a compound lens consists of several simple lenses (''elements'') ...
are called the anterior and posterior poles of the lens.
Modeling optical systems as mathematical transformations
Ingeometrical optics
Geometrical optics, or ray optics, is a model of optics that describes light Wave propagation, propagation in terms of ''ray (optics), rays''. The ray in geometrical optics is an abstract object, abstraction useful for approximating the paths along ...
, for each object ray entering an optical system, a single and unique image ray exits from the system. In mathematical terms, the optical system performs a transformation that maps every object ray to an image ray. The object ray and its associated image ray are said to be ' each other. This term also applies to corresponding pairs of object and image points and planes. The object and image rays, points, and planes are considered to be in two distinct optical spaces, ' and '; additional intermediate optical spaces may be used as well.
Rotationally symmetric optical systems; optical axis, axial points, and meridional planes
An optical system is rotationally symmetric if its imaging properties are unchanged by rotation about some axis. This (unique) axis of rotational symmetry is theoptical axis
An optical axis is an imaginary line that passes through the geometrical center of an optical system such as a camera lens, microscope or telescopic sight. Lens elements often have rotational symmetry about the axis.
The optical axis defines ...
of the system. Optical systems can be folded using plane mirrors; the system is still considered to be rotationally symmetric if it possesses rotational symmetry when unfolded. Any point on the optical axis (in any space) is an '.
Rotational symmetry greatly simplifies the analysis of optical systems, which otherwise must be analyzed in three dimensions. Rotational symmetry allows the system to be analyzed by considering only rays confined to a single transverse plane containing the optical axis. Such a plane is called a '; it is a cross-section through the system.
Ideal, rotationally symmetric, optical imaging system
An , rotationally symmetric, optical imaging system must meet three criteria: #All rays "originating" from object point converge to a single and unique image point; imaging is '' stigmatic''. #Object planes perpendicular to the optical axis are conjugate to image planes perpendicular to the axis. #The image of an object confined to a plane normal to the axis is geometrically similar to the object. In some optical systems imaging is stigmatic for one or perhaps a few object points, but to be an ideal system imaging must be stigmatic for object point. In an ideal system, every object point maps to a different image point. Unlike rays in mathematics, optical rays extend to infinity in both directions. Rays are ' when they are in the part of the optical system to which they apply, and are ' elsewhere. For example, object rays are real on the object side of the optical system, while image rays are real on the image side of the system. In stigmatic imaging, an object ray intersecting any specific point in object space must be conjugate to an image ray intersecting the conjugate point in image space. A consequence is that every point on an object ray is conjugate to some point on the conjugate image ray. Geometrical similarity implies the image is a scale model of the object. There is no restriction on the image's orientation; the image may be inverted or otherwise rotated with respect to the object.Focal and afocal systems, focal points
' systems have no focal points, principal points, or nodal points. In such systems an object ray parallel to the optical axis is conjugate to an image ray parallel to the optical axis. A system is ' if an object ray parallel to the axis is conjugate to an image ray that intersects the optical axis. The intersection of the image ray with the optical axis is the focal point in image space. Focal systems also have an axial object point F such that any ray through F is conjugate to an image ray parallel to the optical axis. F is the object space focal point of the system.Transformation
The transformation between object space and image space is completely defined by the cardinal points of the system, and these points can be used to map any point on the object to its conjugate image point.See also
* Film plane * Pinhole camera model * Radius of curvature (optics) * Vergence (optics)Notes and references