Optimal foraging theory on:
[Wikipedia]
[Google]
[Amazon]
 Optimal foraging theory (OFT) is a
Optimal foraging theory (OFT) is a
"Optimal Foraging Theory: Constraints and Cognitive Processes"
, pp. 105–130 in ''Behavioral Ecology''. University of California, Santa Cruz. The connection between OFT and biological evolution has garnered interest over the past decades. Studies on optimal foraging behaviors at the population level have utilized evolutionary birth-death dynamics models. While these models confirm the existence of objective functions, such as "currency" in certain scenarios, they also prompt questions regarding their applicability in other limits such as high population interactions.
. 1st ed. Monographs in Behavior and Ecology. Princeton University Press. . Currency is defined as the unit that is optimized by the animal. It is also a hypothesis of the costs and benefits that are imposed on that animal.Krebs, J. R. and Davies, N. B. (1989) ''An Introduction to Behavioral Ecology''. 4th ed. Oxford: Blackwell Scientific Publications. For example, a certain forager gains energy from food, but incurs the cost of searching for the food: the time and energy spent searching could have been used instead on other endeavors, such as finding mates or protecting young. It would be in the animal's best interest to maximize its benefits at the lowest cost. Thus, the currency in this situation could be defined as net energy gain per unit time. However, for a different forager, the time it takes to digest the food after eating could be a more significant cost than the time and energy spent looking for food. In this case, the currency could be defined as net energy gain per digestive turnover time instead of net energy gain per unit time. Furthermore, benefits and costs can depend on a forager's community. For example, a forager living in a hive would most likely forage in a manner that would maximize efficiency for its colony rather than itself. By identifying the currency, one can construct a hypothesis about which benefits and costs are important to the forager in question. Constraints are hypotheses about the limitations that are placed on an animal. These limitations can be due to features of the environment or the physiology of the animal and could limit their foraging efficiency. The time that it takes for the forager to travel from the nesting site to the foraging site is an example of a constraint. The maximum number of food items a forager is able to carry back to its nesting site is another example of a constraint. There could also be cognitive constraints on animals, such as limits to learning and memory. The more constraints that one is able to identify in a given system, the more predictive power the model will have. Given the hypotheses about the currency and the constraints, the optimal decision rule is the model's prediction of what the animal's best foraging strategy should be. Possible examples of optimal decision rules could be the optimal number of food items that an animal should carry back to its nesting site or the optimal size of a food item that an animal should feed on. Figure 1, shows an example of how an optimal decision rule could be determined from a graphical model. The curve represents the energy gain per cost (E) for adopting foraging strategy x. Energy gain per cost is the currency being optimized. The constraints of the system determine the shape of this curve. The optimal decision rule (x*) is the strategy for which the currency, energy gain per costs, is the greatest. Optimal foraging models can look very different and become very complex, depending on the nature of the currency and the number of constraints considered. However, the general principles of currency, constraints, and optimal decision rule remain the same for all models.
To test a model, one can compare the predicted strategy to the animal's actual foraging behavior. If the model fits the observed data well, then the hypotheses about the currency and constraints are supported. If the model does not fit the data well, then it is possible that either the currency or a particular constraint has been incorrectly identified.
Given the hypotheses about the currency and the constraints, the optimal decision rule is the model's prediction of what the animal's best foraging strategy should be. Possible examples of optimal decision rules could be the optimal number of food items that an animal should carry back to its nesting site or the optimal size of a food item that an animal should feed on. Figure 1, shows an example of how an optimal decision rule could be determined from a graphical model. The curve represents the energy gain per cost (E) for adopting foraging strategy x. Energy gain per cost is the currency being optimized. The constraints of the system determine the shape of this curve. The optimal decision rule (x*) is the strategy for which the currency, energy gain per costs, is the greatest. Optimal foraging models can look very different and become very complex, depending on the nature of the currency and the number of constraints considered. However, the general principles of currency, constraints, and optimal decision rule remain the same for all models.
To test a model, one can compare the predicted strategy to the animal's actual foraging behavior. If the model fits the observed data well, then the hypotheses about the currency and constraints are supported. If the model does not fit the data well, then it is possible that either the currency or a particular constraint has been incorrectly identified.
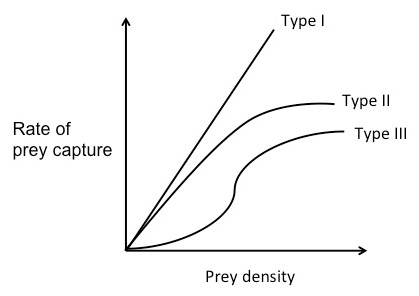 For a Type I functional response curve, the rate of prey capture increases linearly with food density. At low prey densities, the search time is long. Since the predator spends most of its time searching, it eats every prey item it finds. As prey density increases, the predator is able to capture the prey faster and faster. At a certain point, the rate of prey capture is so high, that the predator doesn't have to eat every prey item it encounters. After this point, the predator should choose only the prey items with the highest E/h.
For a Type II functional response curve, the rate of prey capture negatively accelerates as it increases with food density. This is because it assumes that the predator is limited by its capacity to process food. In other words, as the food density increases, handling time increases. At the beginning of the curve, rate of prey capture increases nearly linearly with prey density and there is almost no handling time. As prey density increases, the predator spends less and less time searching for prey and more and more time handling the prey. The rate of prey capture increases less and less, until it finally plateaus. The high number of prey basically "swamps" the predator.
A Type III functional response curve is a sigmoid curve. The rate of prey capture increases at first with prey density at a positively accelerated rate, but then at high densities changes to the negatively accelerated form, similar to that of the Type II curve. At high prey densities (the top of the curve), each new prey item is caught almost immediately. The predator is able to be choosy and does not eat every item it finds. So, assuming that there are two prey types with different profitabilities that are both at high abundance, the predator will choose the item with the higher E/h. However, at low prey densities (the bottom of the curve) the rate of prey capture increases faster than linearly. This means that as the predator feeds and the prey type with the higher E/h becomes less abundant, the predator will start to switch its preference to the prey type with the lower E/h, because that type will be relatively more abundant. This phenomenon is known as prey switching.
For a Type I functional response curve, the rate of prey capture increases linearly with food density. At low prey densities, the search time is long. Since the predator spends most of its time searching, it eats every prey item it finds. As prey density increases, the predator is able to capture the prey faster and faster. At a certain point, the rate of prey capture is so high, that the predator doesn't have to eat every prey item it encounters. After this point, the predator should choose only the prey items with the highest E/h.
For a Type II functional response curve, the rate of prey capture negatively accelerates as it increases with food density. This is because it assumes that the predator is limited by its capacity to process food. In other words, as the food density increases, handling time increases. At the beginning of the curve, rate of prey capture increases nearly linearly with prey density and there is almost no handling time. As prey density increases, the predator spends less and less time searching for prey and more and more time handling the prey. The rate of prey capture increases less and less, until it finally plateaus. The high number of prey basically "swamps" the predator.
A Type III functional response curve is a sigmoid curve. The rate of prey capture increases at first with prey density at a positively accelerated rate, but then at high densities changes to the negatively accelerated form, similar to that of the Type II curve. At high prey densities (the top of the curve), each new prey item is caught almost immediately. The predator is able to be choosy and does not eat every item it finds. So, assuming that there are two prey types with different profitabilities that are both at high abundance, the predator will choose the item with the higher E/h. However, at low prey densities (the bottom of the curve) the rate of prey capture increases faster than linearly. This means that as the predator feeds and the prey type with the higher E/h becomes less abundant, the predator will start to switch its preference to the prey type with the lower E/h, because that type will be relatively more abundant. This phenomenon is known as prey switching.
 The marginal value theorem is a type of optimality model that is often applied to optimal foraging. This theorem is used to describe a situation in which an organism searching for food in a patch must decide when it is economically favorable to leave. While the animal is within a patch, it experiences the law of diminishing returns, where it becomes harder and harder to find prey as time goes on. This may be because the prey is being depleted, the prey begins to take evasive action and becomes harder to catch, or the predator starts crossing its own path more as it searches. This law of diminishing returns can be shown as a curve of energy gain per time spent in a patch (Figure 3). The curve starts off with a steep slope and gradually levels off as prey becomes harder to find. Another important cost to consider is the traveling time between different patches and the nesting site. An animal loses foraging time while it travels and expends energy through its locomotion.
In this model, the currency being optimized is usually net energy gain per unit time. The constraints are the travel time and the shape of the curve of diminishing returns. Graphically, the currency (net energy gain per unit time) is given by the slope of a diagonal line that starts at the beginning of traveling time and intersects the curve of diminishing returns (Figure 3). In order to maximize the currency, one wants the line with the greatest slope that still touches the curve (the tangent line). The place that this line touches the curve provides the optimal decision rule of the amount of time that the animal should spend in a patch before leaving.
The marginal value theorem is a type of optimality model that is often applied to optimal foraging. This theorem is used to describe a situation in which an organism searching for food in a patch must decide when it is economically favorable to leave. While the animal is within a patch, it experiences the law of diminishing returns, where it becomes harder and harder to find prey as time goes on. This may be because the prey is being depleted, the prey begins to take evasive action and becomes harder to catch, or the predator starts crossing its own path more as it searches. This law of diminishing returns can be shown as a curve of energy gain per time spent in a patch (Figure 3). The curve starts off with a steep slope and gradually levels off as prey becomes harder to find. Another important cost to consider is the traveling time between different patches and the nesting site. An animal loses foraging time while it travels and expends energy through its locomotion.
In this model, the currency being optimized is usually net energy gain per unit time. The constraints are the travel time and the shape of the curve of diminishing returns. Graphically, the currency (net energy gain per unit time) is given by the slope of a diagonal line that starts at the beginning of traveling time and intersects the curve of diminishing returns (Figure 3). In order to maximize the currency, one wants the line with the greatest slope that still touches the curve (the tangent line). The place that this line touches the curve provides the optimal decision rule of the amount of time that the animal should spend in a patch before leaving.

 The foraging behavior of the
The foraging behavior of the
Optimal Foraging Theory by Barry Sinervo (1997), Course: "Behavioral Ecology 2013", Department of Ecology and Evolutionary Biology, UCSC
– This Section, of that Course at UCSC, considers OFT and 'Adaptational Hypotheses' ('guided trial and error, instinct'). along with addition subjects such as "Prey Size", "Patch Residence Time", "Patch Quality and Competitors", "Search Strategies", "Risk Aversive Behavior" and foraging practices subject to "Food Limitation". See also: up one Level for the Main Section of the Course, where downloadable PDFs are available (as the Images on that Page seem broken currently). The PDF for the above Link is 26 Pages long (with Images). Food chains Foraging Behavioral ecology
behavioral ecology
Behavioral ecology, also spelled behavioural ecology, is the study of the evolutionary basis for ethology, animal behavior due to ecology, ecological pressures. Behavioral ecology emerged from ethology after Niko Tinbergen outlined Tinbergen's f ...
model that helps predict how an animal behaves when searching for food. Although obtaining food provides the animal with energy, searching for and capturing the food require both energy and time. To maximize fitness, an animal adopts a foraging
Foraging is searching for wild food resources. It affects an animal's fitness because it plays an important role in an animal's ability to survive and reproduce. Foraging theory is a branch of behavioral ecology that studies the foraging behavi ...
strategy that provides the most benefit (energy) for the lowest cost, maximizing the net energy gained. OFT helps predict the best strategy that an animal can use to achieve this goal.
OFT is an ecological application of the optimality model. This theory assumes that the most economically advantageous foraging pattern will be selected for in a species through natural selection
Natural selection is the differential survival and reproduction of individuals due to differences in phenotype. It is a key mechanism of evolution, the change in the Heredity, heritable traits characteristic of a population over generation ...
. When using OFT to model foraging behavior, organisms are said to be maximizing a variable known as the currency, such as the most food per unit time. In addition, the constraints of the environment are other variables that must be considered. Constraints are defined as factors that can limit the forager's ability to maximize the currency. The optimal decision rule, or the organism's best foraging strategy, is defined as the decision that maximizes the currency under the constraints of the environment. Identifying the optimal decision rule is the primary goal of the OFT.Sinervo, Barry (1997)"Optimal Foraging Theory: Constraints and Cognitive Processes"
, pp. 105–130 in ''Behavioral Ecology''. University of California, Santa Cruz. The connection between OFT and biological evolution has garnered interest over the past decades. Studies on optimal foraging behaviors at the population level have utilized evolutionary birth-death dynamics models. While these models confirm the existence of objective functions, such as "currency" in certain scenarios, they also prompt questions regarding their applicability in other limits such as high population interactions.
Building an optimal foraging model
An optimal foraging model generates quantitative predictions of how animals maximize their fitness while they forage. The model building process involves identifying the currency, constraints, and appropriate decision rule for the forager.Stephens, D. W. and Krebs, J. R. (1986. 1st ed. Monographs in Behavior and Ecology. Princeton University Press. . Currency is defined as the unit that is optimized by the animal. It is also a hypothesis of the costs and benefits that are imposed on that animal.Krebs, J. R. and Davies, N. B. (1989) ''An Introduction to Behavioral Ecology''. 4th ed. Oxford: Blackwell Scientific Publications. For example, a certain forager gains energy from food, but incurs the cost of searching for the food: the time and energy spent searching could have been used instead on other endeavors, such as finding mates or protecting young. It would be in the animal's best interest to maximize its benefits at the lowest cost. Thus, the currency in this situation could be defined as net energy gain per unit time. However, for a different forager, the time it takes to digest the food after eating could be a more significant cost than the time and energy spent looking for food. In this case, the currency could be defined as net energy gain per digestive turnover time instead of net energy gain per unit time. Furthermore, benefits and costs can depend on a forager's community. For example, a forager living in a hive would most likely forage in a manner that would maximize efficiency for its colony rather than itself. By identifying the currency, one can construct a hypothesis about which benefits and costs are important to the forager in question. Constraints are hypotheses about the limitations that are placed on an animal. These limitations can be due to features of the environment or the physiology of the animal and could limit their foraging efficiency. The time that it takes for the forager to travel from the nesting site to the foraging site is an example of a constraint. The maximum number of food items a forager is able to carry back to its nesting site is another example of a constraint. There could also be cognitive constraints on animals, such as limits to learning and memory. The more constraints that one is able to identify in a given system, the more predictive power the model will have.
 Given the hypotheses about the currency and the constraints, the optimal decision rule is the model's prediction of what the animal's best foraging strategy should be. Possible examples of optimal decision rules could be the optimal number of food items that an animal should carry back to its nesting site or the optimal size of a food item that an animal should feed on. Figure 1, shows an example of how an optimal decision rule could be determined from a graphical model. The curve represents the energy gain per cost (E) for adopting foraging strategy x. Energy gain per cost is the currency being optimized. The constraints of the system determine the shape of this curve. The optimal decision rule (x*) is the strategy for which the currency, energy gain per costs, is the greatest. Optimal foraging models can look very different and become very complex, depending on the nature of the currency and the number of constraints considered. However, the general principles of currency, constraints, and optimal decision rule remain the same for all models.
To test a model, one can compare the predicted strategy to the animal's actual foraging behavior. If the model fits the observed data well, then the hypotheses about the currency and constraints are supported. If the model does not fit the data well, then it is possible that either the currency or a particular constraint has been incorrectly identified.
Given the hypotheses about the currency and the constraints, the optimal decision rule is the model's prediction of what the animal's best foraging strategy should be. Possible examples of optimal decision rules could be the optimal number of food items that an animal should carry back to its nesting site or the optimal size of a food item that an animal should feed on. Figure 1, shows an example of how an optimal decision rule could be determined from a graphical model. The curve represents the energy gain per cost (E) for adopting foraging strategy x. Energy gain per cost is the currency being optimized. The constraints of the system determine the shape of this curve. The optimal decision rule (x*) is the strategy for which the currency, energy gain per costs, is the greatest. Optimal foraging models can look very different and become very complex, depending on the nature of the currency and the number of constraints considered. However, the general principles of currency, constraints, and optimal decision rule remain the same for all models.
To test a model, one can compare the predicted strategy to the animal's actual foraging behavior. If the model fits the observed data well, then the hypotheses about the currency and constraints are supported. If the model does not fit the data well, then it is possible that either the currency or a particular constraint has been incorrectly identified.
Different feeding systems and classes of predators
Optimal foraging theory is widely applicable to feeding systems throughout the animal kingdom. Under the OFT, ''any'' organism of interest can be viewed as a predator that forages prey. There are different classes of predators that organisms fall into and each class has distinct foraging andpredation
Predation is a biological interaction in which one organism, the predator, kills and eats another organism, its prey. It is one of a family of common List of feeding behaviours, feeding behaviours that includes parasitism and micropredation ...
strategies.
* True predators attack large numbers of prey throughout their life. They kill their prey either immediately or shortly after the attack. They may eat all or only part of their prey. True predators include tigers, lions, whales, shark
Sharks are a group of elasmobranch cartilaginous fish characterized by a ribless endoskeleton, dermal denticles, five to seven gill slits on each side, and pectoral fins that are not fused to the head. Modern sharks are classified within the ...
s and ant
Ants are Eusociality, eusocial insects of the Family (biology), family Formicidae and, along with the related wasps and bees, belong to the Taxonomy (biology), order Hymenoptera. Ants evolved from Vespoidea, vespoid wasp ancestors in the Cre ...
s.
* Grazers eat only a portion of their prey. They harm the prey, but rarely kill it. Grazers include antelope
The term antelope refers to numerous extant or recently extinct species of the ruminant artiodactyl family Bovidae that are indigenous to most of Africa, India, the Middle East, Central Asia, and a small area of Eastern Europe. Antelopes do ...
, cattle, and mosquitoes.
* Parasites
Parasitism is a close relationship between species, where one organism, the parasite, lives (at least some of the time) on or inside another organism, the host, causing it some harm, and is adapted structurally to this way of life. The en ...
, like grazers, eat only a part of their prey (host), but rarely the entire organism. They spend all or large portions of their life cycle living in/on a single host. This intimate relationship is typical of tapeworms, liver fluke
Liver fluke is a collective name of a polyphyletic group of parasitic trematodes under the phylum Platyhelminthes.
They are principally parasites of the liver of various mammals, including humans. Capable of moving along the blood circulation, ...
s, and plant parasites, such as the potato blight.
* Parasitoid
In evolutionary ecology, a parasitoid is an organism that lives in close association with its host (biology), host at the host's expense, eventually resulting in the death of the host. Parasitoidism is one of six major evolutionarily stable str ...
s are mainly typical of wasps
A wasp is any insect of the narrow-waisted suborder Apocrita of the order Hymenoptera which is neither a bee nor an ant; this excludes the broad-waisted sawflies (Symphyta), which look somewhat like wasps, but are in a separate suborder. Th ...
(order ''Hymenoptera''), and some flies (order ''Diptera''). Eggs are laid inside the larvae of other arthropod
Arthropods ( ) are invertebrates in the phylum Arthropoda. They possess an arthropod exoskeleton, exoskeleton with a cuticle made of chitin, often Mineralization (biology), mineralised with calcium carbonate, a body with differentiated (Metam ...
s which hatch and consume the host from the inside, killing it. This unusual predator–host relationship is typical of about 10% of all insects. Many viruses that attack single-celled organisms (such as bacteriophage
A bacteriophage (), also known informally as a phage (), is a virus that infects and replicates within bacteria. The term is derived . Bacteriophages are composed of proteins that Capsid, encapsulate a DNA or RNA genome, and may have structu ...
s) are also parasitoids; they reproduce inside a single host that is inevitably killed by the association.
The optimization of these different foraging and predation strategies can be explained by the optimal foraging theory. In each case, there are costs, benefits, and limitations that ultimately determine the optimal decision rule that the predator should follow.
Optimal diet model
One classical version of the optimal foraging theory is the optimal diet model, which is also known as the prey choice model or the contingency model. In this model, the predator encounters different prey items and decides whether to eat what it has or search for a more profitable prey item. The model predicts that foragers should ignore low profitability prey items when more profitable items are present and abundant. The profitability of a prey item is dependent on several ecological variables. E is the amount of energy (calories) that a prey item provides the predator. Handling time (h) is the amount of time it takes the predator to handle the food, beginning from the time the predator finds the prey item to the time the prey item is eaten. The profitability of a prey item is then defined as E/h. Additionally, search time (S) is the amount of time it takes the predator to find a prey item and is dependent on the abundance of the food and the ease of locating it. In this model, the currency is energy intake per unit time and the constraints include the actual values of E, h, and S, as well as the fact that prey items are encountered sequentially.Model of choice between big and small prey
Using these variables, the optimal diet model can predict how predators choose between two prey types: big prey1 with energy value E1 and handling time h1, and small prey2 with energy value E2 and handling time h2. In order to maximize its overall rate of energy gain, a predator must consider the profitability of the two prey types. If it is assumed that big prey1 is more profitable than small prey2, then E1/h1 > E2/h2. Thus, if the predator encounters prey1, it should always choose to eat it, because of its higher profitability. It should never bother to go searching for prey2. However, if the animal encounters prey2, it should reject it to look for a more profitable prey1, ''unless'' the time it would take to find prey1 is too long and costly for it to be worth it. Thus, the animal should eat prey2 only if E2/h2 > E1/(h1+S1), where S1 is the search time for prey1. Since it is always favorable to choose to eat prey1, the choice to eat prey1 is not dependent on the abundance of prey2. But since the length of S1 (i.e. how difficult it is to find prey1) is logically dependent on the density of prey1, the choice to eat prey2 ''is'' dependent on the abundance of prey1.Generalist and specialist diets
The optimal diet model also predicts that different types of animals should adopt different diets based on variations in search time. This idea is an extension of the model of prey choice that was discussed above. The equation, E2/h2 > E1/(h1+S1), can be rearranged to give: S1 > E1h2)/E2– h1. This rearranged form gives the threshold for how long S1 must be for an animal to choose to eat both prey1 and prey2. Animals that have S1s that reach the threshold are defined as generalists. In nature, generalists include a wide range of prey items in their diet. An example of a generalist is a mouse, which consumes a large variety of seeds, grains, and nuts. In contrast, predators with relatively short S1s are still better off choosing to eat only prey1. These types of animals are defined as specialists and have very exclusive diets in nature. An example of a specialist is thekoala
The koala (''Phascolarctos cinereus''), sometimes inaccurately called the koala bear, is an arboreal herbivorous marsupial native to Australia. It is the only Extant taxon, extant representative of the Family (biology), family ''Phascolar ...
, which solely consumes eucalyptus
''Eucalyptus'' () is a genus of more than 700 species of flowering plants in the family Myrtaceae. Most species of ''Eucalyptus'' are trees, often Mallee (habit), mallees, and a few are shrubs. Along with several other genera in the tribe Eucalyp ...
leaves. In general, different animals across the four functional classes of predators exhibit strategies ranging across a continuum between being a generalist and a specialist. Additionally, since the choice to eat prey2 is dependent on the abundance of prey1 (as discussed earlier), if prey1 becomes so scarce that S1 reaches the threshold, then the animal should switch from exclusively eating prey1 to eating both prey1 and prey2. In other words, if the food within a specialist's diet becomes very scarce, a specialist can sometimes switch to being a generalist.
Functional response curves
As previously mentioned, the amount of time it takes to search for a prey item depends on the density of the prey. Functional response curves show the rate of prey capture as a function of food density and can be used in conjunction with the optimal diet theory to predict foraging behavior of predators. There are three different types of functional response curves. For a Type I functional response curve, the rate of prey capture increases linearly with food density. At low prey densities, the search time is long. Since the predator spends most of its time searching, it eats every prey item it finds. As prey density increases, the predator is able to capture the prey faster and faster. At a certain point, the rate of prey capture is so high, that the predator doesn't have to eat every prey item it encounters. After this point, the predator should choose only the prey items with the highest E/h.
For a Type II functional response curve, the rate of prey capture negatively accelerates as it increases with food density. This is because it assumes that the predator is limited by its capacity to process food. In other words, as the food density increases, handling time increases. At the beginning of the curve, rate of prey capture increases nearly linearly with prey density and there is almost no handling time. As prey density increases, the predator spends less and less time searching for prey and more and more time handling the prey. The rate of prey capture increases less and less, until it finally plateaus. The high number of prey basically "swamps" the predator.
A Type III functional response curve is a sigmoid curve. The rate of prey capture increases at first with prey density at a positively accelerated rate, but then at high densities changes to the negatively accelerated form, similar to that of the Type II curve. At high prey densities (the top of the curve), each new prey item is caught almost immediately. The predator is able to be choosy and does not eat every item it finds. So, assuming that there are two prey types with different profitabilities that are both at high abundance, the predator will choose the item with the higher E/h. However, at low prey densities (the bottom of the curve) the rate of prey capture increases faster than linearly. This means that as the predator feeds and the prey type with the higher E/h becomes less abundant, the predator will start to switch its preference to the prey type with the lower E/h, because that type will be relatively more abundant. This phenomenon is known as prey switching.
For a Type I functional response curve, the rate of prey capture increases linearly with food density. At low prey densities, the search time is long. Since the predator spends most of its time searching, it eats every prey item it finds. As prey density increases, the predator is able to capture the prey faster and faster. At a certain point, the rate of prey capture is so high, that the predator doesn't have to eat every prey item it encounters. After this point, the predator should choose only the prey items with the highest E/h.
For a Type II functional response curve, the rate of prey capture negatively accelerates as it increases with food density. This is because it assumes that the predator is limited by its capacity to process food. In other words, as the food density increases, handling time increases. At the beginning of the curve, rate of prey capture increases nearly linearly with prey density and there is almost no handling time. As prey density increases, the predator spends less and less time searching for prey and more and more time handling the prey. The rate of prey capture increases less and less, until it finally plateaus. The high number of prey basically "swamps" the predator.
A Type III functional response curve is a sigmoid curve. The rate of prey capture increases at first with prey density at a positively accelerated rate, but then at high densities changes to the negatively accelerated form, similar to that of the Type II curve. At high prey densities (the top of the curve), each new prey item is caught almost immediately. The predator is able to be choosy and does not eat every item it finds. So, assuming that there are two prey types with different profitabilities that are both at high abundance, the predator will choose the item with the higher E/h. However, at low prey densities (the bottom of the curve) the rate of prey capture increases faster than linearly. This means that as the predator feeds and the prey type with the higher E/h becomes less abundant, the predator will start to switch its preference to the prey type with the lower E/h, because that type will be relatively more abundant. This phenomenon is known as prey switching.
Predator–prey interaction
Predator–preycoevolution
In biology, coevolution occurs when two or more species reciprocally affect each other's evolution through the process of natural selection. The term sometimes is used for two traits in the same species affecting each other's evolution, as well a ...
often makes it unfavorable for a predator to consume certain prey items, since many anti-predator defenses increase handling time. Examples include porcupine
Porcupines are large rodents with coats of sharp Spine (zoology), spines, or quills, that protect them against predation. The term covers two Family (biology), families of animals: the Old World porcupines of the family Hystricidae, and the New ...
quills, the palatability and digestibility of the poison dart frog, crypsis
In ecology, crypsis is the ability of an animal or a plant to avoid observation or detection by other animals. It may be part of a predation strategy or an antipredator adaptation. Methods include camouflage, nocturnality, subterranean life ...
, and other predator avoidance behaviors. In addition, because toxins may be present in many prey types, predators include a lot of variability in their diets to prevent any one toxin from reaching dangerous levels. Thus, it is possible that an approach focusing only on energy intake may not fully explain an animal's foraging behavior in these situations.
Marginal value theorem and optimal foraging
 The marginal value theorem is a type of optimality model that is often applied to optimal foraging. This theorem is used to describe a situation in which an organism searching for food in a patch must decide when it is economically favorable to leave. While the animal is within a patch, it experiences the law of diminishing returns, where it becomes harder and harder to find prey as time goes on. This may be because the prey is being depleted, the prey begins to take evasive action and becomes harder to catch, or the predator starts crossing its own path more as it searches. This law of diminishing returns can be shown as a curve of energy gain per time spent in a patch (Figure 3). The curve starts off with a steep slope and gradually levels off as prey becomes harder to find. Another important cost to consider is the traveling time between different patches and the nesting site. An animal loses foraging time while it travels and expends energy through its locomotion.
In this model, the currency being optimized is usually net energy gain per unit time. The constraints are the travel time and the shape of the curve of diminishing returns. Graphically, the currency (net energy gain per unit time) is given by the slope of a diagonal line that starts at the beginning of traveling time and intersects the curve of diminishing returns (Figure 3). In order to maximize the currency, one wants the line with the greatest slope that still touches the curve (the tangent line). The place that this line touches the curve provides the optimal decision rule of the amount of time that the animal should spend in a patch before leaving.
The marginal value theorem is a type of optimality model that is often applied to optimal foraging. This theorem is used to describe a situation in which an organism searching for food in a patch must decide when it is economically favorable to leave. While the animal is within a patch, it experiences the law of diminishing returns, where it becomes harder and harder to find prey as time goes on. This may be because the prey is being depleted, the prey begins to take evasive action and becomes harder to catch, or the predator starts crossing its own path more as it searches. This law of diminishing returns can be shown as a curve of energy gain per time spent in a patch (Figure 3). The curve starts off with a steep slope and gradually levels off as prey becomes harder to find. Another important cost to consider is the traveling time between different patches and the nesting site. An animal loses foraging time while it travels and expends energy through its locomotion.
In this model, the currency being optimized is usually net energy gain per unit time. The constraints are the travel time and the shape of the curve of diminishing returns. Graphically, the currency (net energy gain per unit time) is given by the slope of a diagonal line that starts at the beginning of traveling time and intersects the curve of diminishing returns (Figure 3). In order to maximize the currency, one wants the line with the greatest slope that still touches the curve (the tangent line). The place that this line touches the curve provides the optimal decision rule of the amount of time that the animal should spend in a patch before leaving.
Examples of optimal foraging models in animals

Optimal foraging of oystercatchers
Oystercatcher
The oystercatchers are a group of waders forming the family (biology), family Haematopodidae, which has a single genus, ''Haematopus''. They are found on coasts worldwide apart from the polar regions and some tropical regions of Africa and Sout ...
mussel
Mussel () is the common name used for members of several families of bivalve molluscs, from saltwater and Freshwater bivalve, freshwater habitats. These groups have in common a shell whose outline is elongated and asymmetrical compared with other ...
feeding provides an example of how the optimal diet model can be utilized. Oystercatchers forage on mussels and crack them open with their bills. The constraints on these birds are the characteristics of the different mussel sizes. While large mussels provide more energy than small mussels, large mussels are harder to crack open due to their thicker shells. This means that while large mussels have a higher energy content (E), they also have a longer handling time (h). The profitability of any mussel is calculated as E/h. The oystercatchers must decide which mussel size will provide enough nutrition to outweigh the cost and energy required to open it. In their study, Meire and Ervynck tried to model this decision by graphing the relative profitabilities of different sized mussels. They came up with a bell-shaped curve, indicating that moderately sized mussels were the most profitable. However, they observed that if an oystercatcher rejected too many small mussels, the time it took to search for the next suitable mussel greatly increased. This observation shifted their bell-curve to the right (Figure 4). However, while this model predicted that oystercatchers should prefer mussels of 50–55 mm, the observed data showed that oystercatchers actually prefer mussels of 30–45 mm. Meire and Ervynk then realized the preference of mussel size did not depend only on the profitability of the prey, but also on the prey density. After this was accounted for, they found a good agreement between the model's prediction and the observed data.
Optimal foraging in starlings
 The foraging behavior of the
The foraging behavior of the European starling
The common starling (''Sturnus vulgaris''), also known simply as the starling in Great Britain and Ireland, and as European starling in North America, is a medium-sized passerine bird in the starling family, Sturnidae. It is about long and ha ...
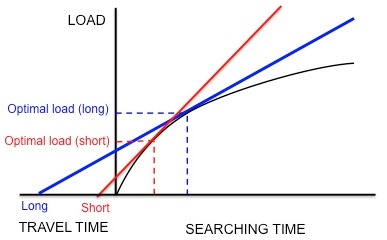
, ''Sturnus vulgaris'', provides an example of how marginal value theorem is used to model optimal foraging. Starlings leave their nests and travel to food patches in search for larval leatherjackets to bring back to their young. The starlings must determine the optimal number of prey items to take back in one trip (i.e. the optimal load size). While the starlings forage within a patch, they experience diminishing returns: the starling is able to hold only so many leatherjackets in its bill, so the speed with which the parent picks up larvae decreases with the number of larvae that it already has in its bill. Thus, the constraints are the shape of the curve of diminishing returns and the travel time (the time it takes to make a round trip from the nest to a patch and back). In addition, the currency is hypothesized to be net energy gain per unit time. Using this currency and the constraints, the optimal load can be predicted by drawing a line tangent to the curve of diminishing returns, as discussed previously (Figure 3).
Kacelnik et al. wanted to determine if this species does indeed optimize net energy gain per unit time as hypothesized. They designed an experiment in which the starlings were trained to collect mealworms from an artificial feeder at different distances from the nest. The researchers artificially generated a fixed curve of diminishing returns for the birds by dropping mealworms at successively longer and longer intervals. The birds continued to collect mealworms as they were presented, until they reached an "optimal" load and flew home. As Figure 5 shows, if the starlings were maximizing net energy gain per unit time, a short travel time would predict a small optimal load and a long travel time would predict a larger optimal load. In agreement with these predictions, Kacelnik found that the longer the distance between the nest and the artificial feeder, the larger the load size. In addition, the observed load sizes quantitatively corresponded very closely to the model's predictions. Other models based on different currencies, such as energy gained per energy spent (i.e. energy efficiency), failed to predict the observed load sizes as accurately. Thus, Kacelnik concluded that starlings maximize net energy gain per unit time. This conclusion was not disproved in later experiments.
Optimal foraging in bees
Worker bee
A worker bee is any female bee that lacks the reproductive capacity of the colony's queen bee and carries out the majority of tasks needed for the functioning of the hive. While worker bees are present in all eusocial bee species, the term is rar ...
s provide another example of the use of marginal value theorem in modeling optimal foraging behavior. Bees forage from flower to flower collecting nectar to carry back to the hive. While this situation is similar to that of the starlings, both the constraints and currency are actually different for the bees.
A bee does not experience diminishing returns because of nectar depletion or any other characteristic of the flowers themselves. The total amount of nectar foraged increases linearly with time spent in a patch. However, the weight of the nectar adds a significant cost to the bee's flight between flowers and its trip back to the hive. Wolf and Schmid-Hempel showed, by experimentally placing varying weights on the backs of bees, that the cost of heavy nectar is so great that it shortens the bees' lifespan. The shorter the lifespan of a worker bee, the less overall time it has to contribute to its colony. Thus, there is a curve of diminishing returns for the net yield of energy that the hive receives as the bee gathers more nectar during one trip.
The cost of heavy nectar also impacts the currency used by the bees. Unlike the starlings in the previous example, bees maximize energy efficiency (energy gained per energy spent) rather than net rate of energy gain (net energy gained per time). This is because the optimal load predicted by maximizing net rate of energy gain is too heavy for the bees and shortens their lifespan, decreasing their overall productivity for the hive, as explained earlier. By maximizing energy efficiency, the bees are able to avoid expending too much energy per trip and are able to live long enough to maximize their lifetime productivity for their hive. In a different paper, Schmid-Hempel showed that the observed relationship between load size and flight time is well correlated with the predictions based on maximizing energy efficiency, but very poorly correlated with the predictions based on maximizing net rate of energy gain.
Optimal foraging in centrarchid fishes
The nature of prey selection by two centrarchids ( white crappie andbluegill
The bluegill (''Lepomis macrochirus''), sometimes referred to as "bream", "brim", "sunny", or, in Texas, "copper nose", is a species of North American freshwater fish, native to and commonly found in streams, rivers, lakes, ponds and wetlands ea ...
) has been presented as a model incorporating optimal foraging strategies by Manatunge and Asaeda. The visual field of the foraging fish as represented by the reactive distance was analysed in detail to estimate the number of prey encounters per search bout. The predicted reactive distances were compared with experimental data. The energetic cost associated with fish foraging behaviour was calculated based on the sequence of events that takes place for each prey consumed. Comparisons of the relative abundance of prey species and size categories in the stomach to the lake environment indicated that both white crappie and bluegill (length < 100 mm) strongly select prey utilizing an energy optimization strategy. In most cases, the fish exclusively selected large ''Daphnia
''Daphnia'' is a genus of small planktonic crustaceans, in length. ''Daphnia'' are members of the Order (biology), order Anomopoda, and are one of the several small aquatic crustaceans commonly called water fleas because their Saltation (gait), ...
'', ignoring evasive prey types (''Cyclops
In Greek mythology and later Roman mythology, the Cyclopes ( ; , ''Kýklōpes'', "Circle-eyes" or "Round-eyes"; singular Cyclops ; , ''Kýklōps'') are giant one-eyed creatures. Three groups of Cyclopes can be distinguished. In Hesiod's ''Th ...
'', diaptomids) and small cladocera. This selectivity is the result of fish actively avoiding prey with high evasion capabilities even though they appear to be high in energetic content and having translated this into optimal selectivity through capture success rates. The energy consideration and visual system, apart from the forager's ability to capture prey, are the major determinants of prey selectivity for large-sized bluegill and white crappie still at planktivorous stages.
Criticism and limitations
Although many studies, such as the ones cited in the examples above, provide quantitative support for optimal foraging theory and demonstrate its usefulness, the model has received criticism regarding its validity and limitations. First, optimal foraging theory relies on the assumption that natural selection will optimize foraging strategies of organisms. However, natural selection is not an all-powerful force that produces perfect designs, but rather a passive process of selection for genetically based traits that increase organisms'reproductive success
Reproductive success is an individual's production of offspring per breeding event or lifetime. This is not limited by the number of offspring produced by one individual, but also the reproductive success of these offspring themselves.
Reproduct ...
. Given that genetics
Genetics is the study of genes, genetic variation, and heredity in organisms.Hartl D, Jones E (2005) It is an important branch in biology because heredity is vital to organisms' evolution. Gregor Mendel, a Moravian Augustinians, Augustinian ...
involves interactions between loci, recombination, and other complexities, there is no guarantee that natural selection can optimize a specific behavioral parameter.Gray, Russell D. "Faith and Foraging: A Critique of the "Paradigm Argument from Design"" p. 198 in ''Foraging Behavior''. Ed. Alan C. Kamil, John R. Krebs, and H. Robald Pulliam. New York: Plenum
In addition, OFT also assumes that foraging behaviors are able to be freely shaped by natural selection, because these behaviors are independent from other activities of the organism. However, given that organisms are integrated systems, rather than mechanical aggregates of parts, this is not always the case. For example, the need to avoid predators may constrain foragers to feed less than the optimal rate. Thus, an organism's foraging behaviors may not be optimized as OFT would predict, because they are not independent from other behaviors.
Another limitation of OFT is that it lacks precision in practice. In theory, an optimal foraging model gives researchers specific, quantitative predictions about a predator's optimal decision rule based on the hypotheses about the currency and constraints of the system. However, in reality, it is difficult to define basic concepts like prey type, encounter rates, or even a patch as the forager perceives them. Thus, while the variables of OFT can seem consistent theoretically, in practice, they can be arbitrary and difficult to measure.
Furthermore, although the premise of OFT is to maximize an organism's fitness, many studies show only correlations between observed and predicted foraging behavior and stop short of testing whether the animal's behavior actually increases its reproductive fitness. It is possible that in certain cases, there is no correlation between foraging returns and reproductive success at all. Without accounting for this possibility, many studies using the OFT remain incomplete and fail to address and test the main point of the theory.
One of the most imperative critiques of OFT is that it may not be truly testable. This issue arises whenever there is a discrepancy between the model's predictions and the actual observations. It is difficult to tell whether the model is fundamentally wrong or whether a specific variable has been inaccurately identified or left out. Because it is possible to add endless plausible modifications to the model, the model of optimality may never be rejected. This creates the problem of researchers shaping their model to fit their observations, rather than rigorously testing their hypotheses about the animal's foraging behavior.
In archaeology
Optimal foraging theory has been used to predict animal behaviour when searching for food, but can also be used for humans (specifically hunter-gatherers). Food provides energy but costs energy to obtain. Foraging strategy must provide the most benefit for the lowest cost – it is a balance between nutritional value and energy required. The currency of optimal foraging theory is energy because it is an essential component for organisms, but it is also the downfall of optimal foraging theory in regard to archaeology. Optimal foraging theory assumes that behaviour is to some extent influenced by genetic makeup. However, this can be hard to accepted in relation to complex animals with a high behavioral flexibility. Human behaviour is not always predictable when using the premise of optimal foraging theory – hunter-gatherers could for ritual or feasting purposes choose a game which would not benefit energy, but would benefit other needs. The goals and currencies of humans can often change due to behavioral flexibility. These changes can occur over a long time, over a season or during a hunt. Optimal foraging theory must therefore be more complex and introduces more goals and constraints to match the complex decision-making processes employed by humans. The decision-making processes can furthermore be influenced by long-term and short-term experiences and these experiences can then further influence others. But optimal foraging theory has helped archaeology in generating new interpretations of patterns in the archaeological record and thinking about human behaviours in greater detail. Optimal foraging theory has also given archaeology a better insight into the cost and benefits of different resources.References
{{Reflist, 30emFurther reading
Optimal Foraging Theory by Barry Sinervo (1997), Course: "Behavioral Ecology 2013", Department of Ecology and Evolutionary Biology, UCSC
– This Section, of that Course at UCSC, considers OFT and 'Adaptational Hypotheses' ('guided trial and error, instinct'). along with addition subjects such as "Prey Size", "Patch Residence Time", "Patch Quality and Competitors", "Search Strategies", "Risk Aversive Behavior" and foraging practices subject to "Food Limitation". See also: up one Level for the Main Section of the Course, where downloadable PDFs are available (as the Images on that Page seem broken currently). The PDF for the above Link is 26 Pages long (with Images). Food chains Foraging Behavioral ecology