Nyquist stability criterion on:
[Wikipedia]
[Google]
[Amazon]
 In
In
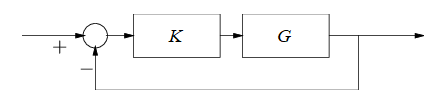 Our goal is to, through this process, check for the stability of the transfer function of our unity feedback system with gain ''k'', which is given by
:
That is, we would like to check whether the characteristic equation of the above transfer function, given by
:
has zeros outside the open left-half-plane (commonly initialized as OLHP).
We suppose that we have a clockwise (i.e. negatively oriented) contour enclosing the right half plane, with indentations as needed to avoid passing through zeros or poles of the function . Cauchy's
Our goal is to, through this process, check for the stability of the transfer function of our unity feedback system with gain ''k'', which is given by
:
That is, we would like to check whether the characteristic equation of the above transfer function, given by
:
has zeros outside the open left-half-plane (commonly initialized as OLHP).
We suppose that we have a clockwise (i.e. negatively oriented) contour enclosing the right half plane, with indentations as needed to avoid passing through zeros or poles of the function . Cauchy's
Applets with modifiable parameters
EIS Spectrum Analyser - a freeware program for analysis and simulation of impedance spectra
for creating a Nyquist plot of a frequency response of a dynamic system model.
PID Nyquist plot shaping
- free interactive virtual tool, control loop simulator
Signal processing Classical control theory Stability theory
control theory
Control theory is a field of mathematics that deals with the control system, control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive ...
and stability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions. The heat equation, for example, is a stable partial diffe ...
, the Nyquist stability criterion or Strecker–Nyquist stability criterion, independently discovered by the German electrical engineer at Siemens
Siemens AG ( ) is a German multinational conglomerate corporation and the largest industrial manufacturing company in Europe headquartered in Munich with branch offices abroad.
The principal divisions of the corporation are ''Industry'', ''E ...
in 1930 and the Swedish-American electrical engineer Harry Nyquist
Harry Nyquist (, ; February 7, 1889 – April 4, 1976) was a Swedish-American physicist and electronic engineer who made important contributions to communication theory.
Personal life
Nyquist was born in the village Nilsby of the parish Stora ...
at Bell Telephone Laboratories in 1932, is a graphical technique for determining the stability of a dynamical system
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water i ...
. Because it only looks at the Nyquist plot of the open loop systems, it can be applied without explicitly computing the poles and zeros of either the closed-loop or open-loop system (although the number of each type of right-half-plane singularities must be known). As a result, it can be applied to systems defined by non-rational function
In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be ...
s, such as systems with delays. In contrast to Bode plots, it can handle transfer functions with right half-plane singularities. In addition, there is a natural generalization to more complex systems with multiple inputs and multiple outputs, such as control systems for airplanes.
The Nyquist criterion is widely used in electronics
The field of electronics is a branch of physics and electrical engineering that deals with the emission, behaviour and effects of electrons using electronic devices. Electronics uses active devices to control electron flow by amplification ...
and control system engineering, as well as other fields, for designing and analyzing systems with feedback
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause-and-effect that forms a circuit or loop. The system can then be said to ''feed back'' into itself. The notion of cause-and-effect has to be handled ...
. While Nyquist is one of the most general stability tests, it is still restricted to linear time-invariant (LTI) systems. Non-linear systems must use more complex stability criteria, such as Lyapunov or the circle criterion. While Nyquist is a graphical technique, it only provides a limited amount of intuition for why a system is stable or unstable, or how to modify an unstable system to be stable. Techniques like Bode plots, while less general, are sometimes a more useful design tool.
Nyquist plot
A Nyquist plot is aparametric plot
In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric o ...
of a frequency response used in automatic control and signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing '' signals'', such as sound, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, ...
. The most common use of Nyquist plots is for assessing the stability of a system with feedback
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause-and-effect that forms a circuit or loop. The system can then be said to ''feed back'' into itself. The notion of cause-and-effect has to be handled ...
. In Cartesian coordinates
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in ...
, the real part of the transfer function is plotted on the ''X''-axis while the imaginary part is plotted on the ''Y''-axis. The frequency is swept as a parameter, resulting in a plot per frequency. The same plot can be described using polar coordinates
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to th ...
, where gain
Gain or GAIN may refer to:
Science and technology
* Gain (electronics), an electronics and signal processing term
* Antenna gain
* Gain (laser), the amplification involved in laser emission
* Gain (projection screens)
* Information gain in de ...
of the transfer function is the radial coordinate, and the phase of the transfer function is the corresponding angular coordinate. The Nyquist plot is named after Harry Nyquist
Harry Nyquist (, ; February 7, 1889 – April 4, 1976) was a Swedish-American physicist and electronic engineer who made important contributions to communication theory.
Personal life
Nyquist was born in the village Nilsby of the parish Stora ...
, a former engineer at Bell Laboratories
Nokia Bell Labs, originally named Bell Telephone Laboratories (1925–1984),
then AT&T Bell Laboratories (1984–1996)
and Bell Labs Innovations (1996–2007),
is an American industrial Research and development, research and scientific developm ...
.
Assessment of the stability of a closed-loop negative feedback
Negative feedback (or balancing feedback) occurs when some function of the output of a system, process, or mechanism is fed back in a manner that tends to reduce the fluctuations in the output, whether caused by changes in the input or by othe ...
system is done by applying the Nyquist stability criterion to the Nyquist plot of the open-loop system (i.e. the same system without its feedback loop). This method is easily applicable even for systems with delays and other non-rational transfer functions, which may appear difficult to analyze with other methods. Stability is determined by looking at the number of encirclements of the point (−1, 0). The range of gains over which the system will be stable can be determined by looking at crossings of the real axis.
The Nyquist plot can provide some information about the shape of the transfer function. For instance, the plot provides information on the difference between the number of zeros and poles of the transfer function by the angle at which the curve approaches the origin.
When drawn by hand, a cartoon version of the Nyquist plot is sometimes used, which shows the linearity of the curve, but where coordinates are distorted to show more detail in regions of interest. When plotted computationally, one needs to be careful to cover all frequencies of interest. This typically means that the parameter is swept logarithmically, in order to cover a wide range of values.
Background
The mathematics uses theLaplace transform
In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace (), is an integral transform that converts a function of a real variable (usually t, in the '' time domain'') to a function of a complex variable s (in the ...
, which transforms integrals and derivatives in the time domain to simple multiplication and division in the ''s'' domain.
We consider a system whose transfer function is ; when placed in a closed loop with negative feedback , the closed loop transfer function (CLTF) then becomes . Stability can be determined by examining the roots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients.
Root or roots may also refer to:
Art, entertainment, and media
* ''The Root'' (magazine), an online magazine focusing ...
of the desensitivity factor polynomial , e.g. using the Routh array, but this method is somewhat tedious. Conclusions can also be reached by examining the open loop transfer function (OLTF) , using its Bode plots or, as here, its polar plot using the Nyquist criterion, as follows.
Any Laplace domain transfer function can be expressed as the ratio of two polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An exampl ...
s:
The roots of are called the ''zeros'' of , and the roots of are the ''poles'' of . The poles of are also said to be the roots of the ''characteristic equation'' .
The stability of is determined by the values of its poles: for stability, the real part of every pole must be negative. If is formed by closing a negative unity feedback loop around the open-loop transfer function , then the roots of the characteristic equation are also the zeros of , or simply the roots of .
Cauchy's argument principle
Fromcomplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates Function (mathematics), functions of complex numbers. It is helpful in many branches of mathemati ...
, a contour drawn in the complex plane, encompassing but not passing through any number of zeros and poles of a function , can be mapped to another plane (named plane) by the function . Precisely, each complex point in the contour is mapped to the point in the new plane yielding a new contour.
The Nyquist plot of , which is the contour will encircle the point of the plane times, where by Cauchy's argument principle. Here and are, respectively, the number of zeros of and poles of inside the contour . Note that we count encirclements in the plane in the same sense as the contour and that encirclements in the opposite direction are ''negative'' encirclements. That is, we consider clockwise encirclements to be positive and counterclockwise encirclements to be negative.
Instead of Cauchy's argument principle, the original paper by Harry Nyquist
Harry Nyquist (, ; February 7, 1889 – April 4, 1976) was a Swedish-American physicist and electronic engineer who made important contributions to communication theory.
Personal life
Nyquist was born in the village Nilsby of the parish Stora ...
in 1932 uses a less elegant approach. The approach explained here is similar to the approach used by Leroy MacColl (Fundamental theory of servomechanisms 1945) or by Hendrik Bode (Network analysis and feedback amplifier design 1945), both of whom also worked for Bell Laboratories
Nokia Bell Labs, originally named Bell Telephone Laboratories (1925–1984),
then AT&T Bell Laboratories (1984–1996)
and Bell Labs Innovations (1996–2007),
is an American industrial Research and development, research and scientific developm ...
. This approach appears in most modern textbooks on control theory.
The Nyquist criterion
We first construct the Nyquist contour, a contour that encompasses the right-half of the complex plane: * a path traveling up the axis, from to . * a semicircular arc, with radius , that starts at and travels clock-wise to . The Nyquist contour mapped through the function yields a plot of in the complex plane. By the argument principle, the number of clockwise encirclements of the origin must be the number of zeros of in the right-half complex plane minus the number of poles of in the right-half complex plane. If instead, the contour is mapped through the open-loop transfer function , the result is the Nyquist Plot of . By counting the resulting contour's encirclements of −1, we find the difference between the number of poles and zeros in the right-half complex plane of . Recalling that the zeros of are the poles of the closed-loop system, and noting that the poles of are same as the poles of , we now state the ''Nyquist Criterion'':''Given a Nyquist contour , let be the number of poles of encircled by , and be the number of zeros of encircled by . Alternatively, and more importantly, if is the number of poles of the closed loop system in the right half plane, and is the number of poles of the open-loop transfer function in the right half plane, the resultant contour in the -plane, shall encircle (clockwise) the point times such that .''If the system is originally open-loop unstable, feedback is necessary to stabilize the system. Right-half-plane (RHP) poles represent that instability. For closed-loop stability of a system, the number of closed-loop roots in the right half of the ''s''-plane must be zero. Hence, the number of counter-clockwise encirclements about must be equal to the number of open-loop poles in the RHP. Any clockwise encirclements of the critical point by the open-loop frequency response (when judged from low frequency to high frequency) would indicate that the feedback control system would be destabilizing if the loop were closed. (Using RHP zeros to "cancel out" RHP poles does not remove the instability, but rather ensures that the system will remain unstable even in the presence of feedback, since the closed-loop roots travel between open-loop poles and zeros in the presence of feedback. In fact, the RHP zero can make the unstable pole unobservable and therefore not stabilizable through feedback.)
The Nyquist criterion for systems with poles on the imaginary axis
The above consideration was conducted with an assumption that the open-loop transfer function does not have any pole on the imaginary axis (i.e. poles of the form ). This results from the requirement of theargument principle
In complex analysis, the argument principle (or Cauchy's argument principle) relates the difference between the number of zeros and poles of a meromorphic function to a contour integral of the function's logarithmic derivative.
Specifically, i ...
that the contour cannot pass through any pole of the mapping function. The most common case are systems with integrators (poles at zero).
To be able to analyze systems with poles on the imaginary axis, the Nyquist Contour can be modified to avoid passing through the point . One way to do it is to construct a semicircular arc with radius around , that starts at and travels anticlockwise to . Such a modification implies that the phasor travels along an arc of infinite radius by , where is the multiplicity of the pole on the imaginary axis.
Mathematical derivation
 Our goal is to, through this process, check for the stability of the transfer function of our unity feedback system with gain ''k'', which is given by
:
That is, we would like to check whether the characteristic equation of the above transfer function, given by
:
has zeros outside the open left-half-plane (commonly initialized as OLHP).
We suppose that we have a clockwise (i.e. negatively oriented) contour enclosing the right half plane, with indentations as needed to avoid passing through zeros or poles of the function . Cauchy's
Our goal is to, through this process, check for the stability of the transfer function of our unity feedback system with gain ''k'', which is given by
:
That is, we would like to check whether the characteristic equation of the above transfer function, given by
:
has zeros outside the open left-half-plane (commonly initialized as OLHP).
We suppose that we have a clockwise (i.e. negatively oriented) contour enclosing the right half plane, with indentations as needed to avoid passing through zeros or poles of the function . Cauchy's argument principle
In complex analysis, the argument principle (or Cauchy's argument principle) relates the difference between the number of zeros and poles of a meromorphic function to a contour integral of the function's logarithmic derivative.
Specifically, i ...
states that
:
Where denotes the number of zeros of enclosed by the contour and denotes the number of poles of by the same contour. Rearranging, we have
, which is to say
:
We then note that has exactly the same poles as . Thus, we may find by counting the poles of that appear within the contour, that is, within the open right half plane (ORHP).
We will now rearrange the above integral via substitution. That is, setting , we have
:
We then make a further substitution, setting . This gives us
:
We now note that gives us the image of our contour under , which is to say our Nyquist plot. We may further reduce the integral
:
by applying Cauchy's integral formula. In fact, we find that the above integral corresponds precisely to the number of times the Nyquist plot encircles the point clockwise. Thus, we may finally state that
:
We thus find that as defined above corresponds to a stable unity-feedback system when , as evaluated above, is equal to 0.
Summary
* If the open-loop transfer function has a zero pole of multiplicity , then the Nyquist plot has a discontinuity at . During further analysis it should be assumed that the phasor travels times clockwise along a semicircle of infinite radius. After applying this rule, the zero poles should be neglected, i.e. if there are no other unstable poles, then the open-loop transfer function should be considered stable. * If the open-loop transfer function is stable, then the closed-loop system is unstable, if and only if, the Nyquist plot encircle the point −1 at least once. * If the open-loop transfer function is ''unstable'', then for the closed-loop system to be stable, there must be one ''counter''-clockwise encirclement of −1 for each pole of in the right-half of the complex plane. * The number of surplus encirclements (''N'' + ''P'' greater than 0) is exactly the number of unstable poles of the closed-loop system. * However, if the graph happens to pass through the point , then deciding upon even the marginal stability of the system becomes difficult and the only conclusion that can be drawn from the graph is that there exist zeros on the axis.See also
* BIBO stability * Bode plot * Routh–Hurwitz stability criterion * Gain margin * Nichols plot * Hall circles * Phase margin *Barkhausen stability criterion
In electronics, the Barkhausen stability criterion is a mathematical condition to determine when a linear electronic circuit will oscillate. It was put forth in 1921 by German physicist Heinrich Georg Barkhausen (1881–1956). It is widely u ...
* Circle criterion
* Control engineering
Control engineering or control systems engineering is an engineering discipline that deals with control systems, applying control theory to design equipment and systems with desired behaviors in control environments. The discipline of controls o ...
* Hankel singular value
References
Further reading
* Faulkner, E. A. (1969): ''Introduction to the Theory of Linear Systems''; Chapman & Hall; * Pippard, A. B. (1985): ''Response & Stability''; Cambridge University Press; * Gessing, R. (2004): ''Control fundamentals''; Silesian University of Technology; * Franklin, G. (2002): ''Feedback Control of Dynamic Systems''; Prentice Hall,External links
{{Commons category, Nyquist plotsApplets with modifiable parameters
EIS Spectrum Analyser - a freeware program for analysis and simulation of impedance spectra
for creating a Nyquist plot of a frequency response of a dynamic system model.
PID Nyquist plot shaping
- free interactive virtual tool, control loop simulator
Signal processing Classical control theory Stability theory