Non-Euclidean geometry on:
[Wikipedia]
[Google]
[Amazon]
 In
In
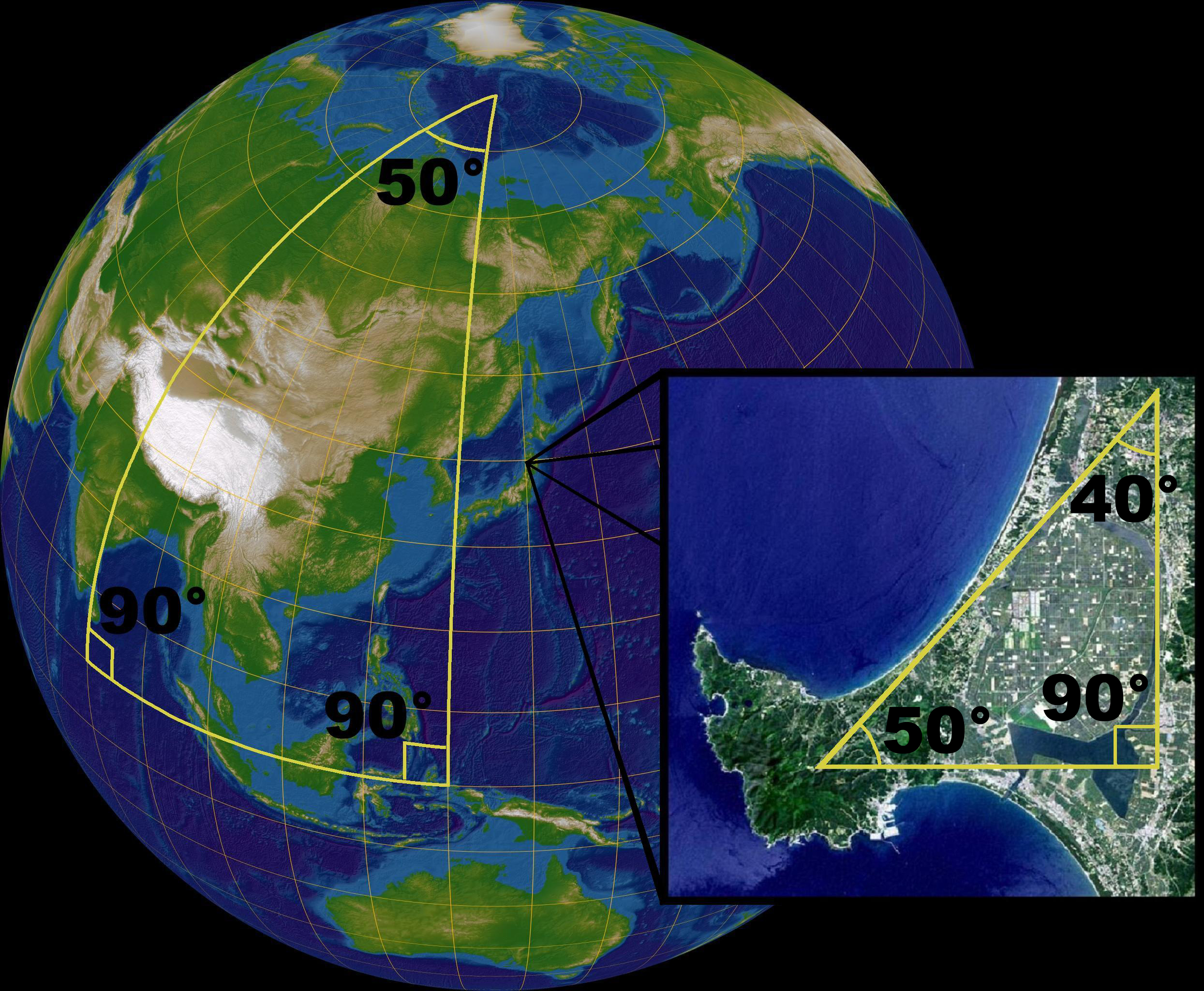 Two dimensional Euclidean geometry is
Two dimensional Euclidean geometry is

 Euclidean and non-Euclidean geometries naturally have many similar properties, namely those that do not depend upon the nature of parallelism. This commonality is the subject of
Euclidean and non-Euclidean geometries naturally have many similar properties, namely those that do not depend upon the nature of parallelism. This commonality is the subject of
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, non-Euclidean geometry consists of two geometries based on axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or f ...
s closely related to those that specify Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry: the ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small ...
. As Euclidean geometry lies at the intersection of metric geometry
In mathematics, a metric space is a set together with a notion of ''distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general settin ...
and affine geometry
In mathematics, affine geometry is what remains of Euclidean geometry when ignoring (mathematicians often say "forgetting") the metric notions of distance and angle.
As the notion of '' parallel lines'' is one of the main properties that is ...
, non-Euclidean geometry arises by either replacing the parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's ''Elements'', is a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:
''If a line segment ...
with an alternative, or relaxing the metric requirement. In the former case, one obtains hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P ...
and elliptic geometry
Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines ...
, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras, which give rise to kinematic geometries that have also been called non-Euclidean geometry.
The essential difference between the metric geometries is the nature of parallel
Parallel is a geometric term of location which may refer to:
Computing
* Parallel algorithm
* Parallel computing
* Parallel metaheuristic
* Parallel (software), a UNIX utility for running programs in parallel
* Parallel Sysplex, a cluster of ...
lines. Euclid
Euclid (; grc-gre, Wikt:Εὐκλείδης, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Euclid's Elements, Elements'' trea ...
's fifth postulate, the parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's ''Elements'', is a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:
''If a line segment ...
, is equivalent to Playfair's postulate
In geometry, Playfair's axiom is an axiom that can be used instead of the fifth postulate of Euclid (the parallel postulate):
''In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the ...
, which states that, within a two-dimensional plane, for any given line and a point ''A'', which is not on , there is exactly one line through ''A'' that does not intersect . In hyperbolic geometry, by contrast, there are infinitely
Infinity is that which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .
Since the time of the ancient Greeks, the philosophical nature of infinity was the subject of many discussions amo ...
many lines through ''A'' not intersecting , while in elliptic geometry, any line through ''A'' intersects .
Another way to describe the differences between these geometries is to consider two straight lines indefinitely extended in a two-dimensional plane that are both perpendicular
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the ''perpendicular symbol'', ⟂. It can ...
to a third line (in the same plane):
*In Euclidean geometry, the lines remain at a constant distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects or points are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two counties over"). ...
from each other (meaning that a line drawn perpendicular to one line at any point will intersect the other line and the length of the line segment joining the points of intersection remains constant) and are known as parallels.
*In hyperbolic geometry, they "curve away" from each other, increasing in distance as one moves further from the points of intersection with the common perpendicular; these lines are often called ultraparallels.
*In elliptic geometry, the lines "curve toward" each other and intersect.
History
Background
Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry: the ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small ...
, named after the Greek mathematician Euclid
Euclid (; grc-gre, Wikt:Εὐκλείδης, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Euclid's Elements, Elements'' trea ...
, includes some of the oldest known mathematics, and geometries that deviated from this were not widely accepted as legitimate until the 19th century.
The debate that eventually led to the discovery of the non-Euclidean geometries began almost as soon as Euclid wrote '' Elements''. In the ''Elements'', Euclid begins with a limited number of assumptions (23 definitions, five common notions, and five postulates) and seeks to prove all the other results (proposition
In logic and linguistics, a proposition is the meaning of a declarative sentence. In philosophy, " meaning" is understood to be a non-linguistic entity which is shared by all sentences with the same meaning. Equivalently, a proposition is the no ...
s) in the work. The most notorious of the postulates is often referred to as "Euclid's Fifth Postulate", or simply the ''parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's ''Elements'', is a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:
''If a line segment ...
'', which in Euclid's original formulation is:
If a straight line falls on two straight lines in such a manner that the interior angles on the same side are together less than two right angles, then the straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.Other mathematicians have devised simpler forms of this property. Regardless of the form of the postulate, however, it consistently appears more complicated than Euclid's other postulates:
1. To draw a straight line from any point to any point. 2. To produceFor at least a thousand years,xtend Xtend is a general-purpose high-level programming language for the Java Virtual Machine. Syntactically and semantically Xtend has its roots in the Java programming language but focuses on a more concise syntax and some additional functionality ...a finite straight line continuously in a straight line. 3. To describe a circle with any centre and distance adius 4. That all right angles are equal to one another.
geometer
A geometer is a mathematician whose area of study is geometry.
Some notable geometers and their main fields of work, chronologically listed, are:
1000 BCE to 1 BCE
* Baudhayana (fl. c. 800 BC) – Euclidean geometry, geometric algebra
* ...
s were troubled by the disparate complexity of the fifth postulate, and believed it could be proved as a theorem from the other four. Many attempted to find a proof by contradiction
In logic and mathematics, proof by contradiction is a form of proof that establishes the truth or the validity of a proposition, by showing that assuming the proposition to be false leads to a contradiction. Proof by contradiction is also known ...
, including Ibn al-Haytham
Ḥasan Ibn al-Haytham, Latinized as Alhazen (; full name ; ), was a medieval mathematician, astronomer, and physicist of the Islamic Golden Age from present-day Iraq.For the description of his main fields, see e.g. ("He is one of the pri ...
(Alhazen, 11th century), Omar Khayyám (12th century), Nasīr al-Dīn al-Tūsī
Muhammad ibn Muhammad ibn al-Hasan al-Tūsī ( fa, محمد ابن محمد ابن حسن طوسی 18 February 1201 – 26 June 1274), better known as Nasir al-Din al-Tusi ( fa, نصیر الدین طوسی, links=no; or simply Tusi in the West ...
(13th century), and Giovanni Girolamo Saccheri
Giovanni Girolamo Saccheri (; 5 September 1667 – 25 October 1733) was an Italian Jesuit priest, scholastic philosopher, and mathematician.
Saccheri was born in Sanremo. He entered the Jesuit order in 1685 and was ordained as a priest in 1694 ...
(18th century).
The theorems of Ibn al-Haytham, Khayyam and al-Tusi on quadrilateral
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''latus'', meaning "side". It is also called a tetragon, ...
s, including the Lambert quadrilateral
In geometry, a Lambert quadrilateral (also known as Ibn al-Haytham–Lambert quadrilateral), is a quadrilateral in which three of its angles are right angles. Historically, the fourth angle of a Lambert quadrilateral was of considerable interest s ...
and Saccheri quadrilateral
A Saccheri quadrilateral (also known as a Khayyam–Saccheri quadrilateral) is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book ''Euclides ab omni na ...
, were "the first few theorems of the hyperbolic
Hyperbolic is an adjective describing something that resembles or pertains to a hyperbola (a curve), to hyperbole (an overstatement or exaggeration), or to hyperbolic geometry.
The following phenomena are described as ''hyperbolic'' because they ...
and the elliptic geometries". These theorems along with their alternative postulates, such as Playfair's axiom
In geometry, Playfair's axiom is an axiom that can be used instead of the fifth postulate of Euclid (the parallel postulate):
''In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the ...
, played an important role in the later development of non-Euclidean geometry. These early attempts at challenging the fifth postulate had a considerable influence on its development among later European geometers, including Witelo
Vitello ( pl, Witelon; german: Witelo; – 1280/1314) was a friar, theologian, natural philosopher and an important figure in the history of philosophy in Poland.
Name
Vitello's name varies with some sources. In earlier publications he was quo ...
, Levi ben Gerson
Levi ben Gershon (1288 – 20 April 1344), better known by his Graecized name as Gersonides, or by his Latinized name Magister Leo Hebraeus, or in Hebrew by the abbreviation of first letters as ''RaLBaG'', was a medieval French Jewish philosoph ...
, Alfonso
Alphons (Latinized ''Alphonsus'', ''Adelphonsus'', or ''Adefonsus'') is a male given name recorded from the 8th century (Alfonso I of Asturias, r. 739–757) in the Christian successor states of the Visigothic kingdom in the Iberian peninsula. ...
, John Wallis and Saccheri. All of these early attempts made at trying to formulate non-Euclidean geometry, however, provided flawed proofs of the parallel postulate, containing assumptions that were essentially equivalent to the parallel postulate. These early attempts did, however, provide some early properties of the hyperbolic and elliptic geometries.
Khayyam, for example, tried to derive it from an equivalent postulate he formulated from "the principles of the Philosopher" (Aristotle
Aristotle (; grc-gre, Ἀριστοτέλης ''Aristotélēs'', ; 384–322 BC) was a Greek philosopher and polymath during the Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatetic school of phil ...
): "Two convergent straight lines intersect and it is impossible for two convergent straight lines to diverge in the direction in which they converge." Khayyam then considered the three cases right, obtuse, and acute that the summit angles of a Saccheri quadrilateral can take and after proving a number of theorems about them, he correctly refuted the obtuse and acute cases based on his postulate and hence derived the classic postulate of Euclid, which he didn't realize was equivalent to his own postulate. Another example is al-Tusi's son, Sadr al-Din (sometimes known as "Pseudo-Tusi"), who wrote a book on the subject in 1298, based on al-Tusi's later thoughts, which presented another hypothesis equivalent to the parallel postulate. "He essentially revised both the Euclidean system of axioms and postulates and the proofs of many propositions from the ''Elements''." His work was published in Rome
, established_title = Founded
, established_date = 753 BC
, founder = King Romulus (legendary)
, image_map = Map of comune of Rome (metropolitan city of Capital Rome, region Lazio, Italy).svg
, map_caption ...
in 1594 and was studied by European geometers, including SaccheriVictor J. Katz (1998), ''History of Mathematics: An Introduction'', p. 270–271, Addison–Wesley
Addison-Wesley is an American publisher of textbooks and computer literature. It is an imprint of Pearson PLC, a global publishing and education company. In addition to publishing books, Addison-Wesley also distributes its technical titles throu ...
, : "But in a manuscript probably written by his son Sadr al-Din in 1298, based on Nasir al-Din's later thoughts on the subject, there is a new argument based on another hypothesis, also equivalent to Euclid's, ..The importance of this latter work is that it was published in Rome in 1594 and was studied by European geometers. In particular, it became the starting point for the work of Saccheri and ultimately for the discovery of non-Euclidean geometry."who criticised this work as well as that of Wallis.
Giordano Vitale
Giordano Vitale or Vitale Giordano (October 15, 1633 – November 3, 1711) was an Italian mathematician. He is best known for his theorem on Saccheri quadrilaterals. He may also be referred to as Vitale Giordani, Vitale Giordano da Bitonto, an ...
, in his book ''Euclide restituo'' (1680, 1686), used the Saccheri quadrilateral to prove that if three points are equidistant on the base AB and the summit CD, then AB and CD are everywhere equidistant.
In a work titled ''Euclides ab Omni Naevo Vindicatus'' (''Euclid Freed from All Flaws''), published in 1733, Saccheri quickly discarded elliptic geometry as a possibility (some others of Euclid's axioms must be modified for elliptic geometry to work) and set to work proving a great number of results in hyperbolic geometry.
He finally reached a point where he believed that his results demonstrated the impossibility of hyperbolic geometry. His claim seems to have been based on Euclidean presuppositions, because no ''logical'' contradiction was present. In this attempt to prove Euclidean geometry he instead unintentionally discovered a new viable geometry, but did not realize it.
In 1766 Johann Lambert
Johann Heinrich Lambert (, ''Jean-Henri Lambert'' in French language, French; 26 or 28 August 1728 – 25 September 1777) was a polymath from the Republic of Mulhouse, generally referred to as either Switzerland, Swiss or France, French, who made i ...
wrote, but did not publish, ''Theorie der Parallellinien'' in which he attempted, as Saccheri did, to prove the fifth postulate. He worked with a figure now known as a ''Lambert quadrilateral'', a quadrilateral with three right angles (can be considered half of a Saccheri quadrilateral). He quickly eliminated the possibility that the fourth angle is obtuse, as had Saccheri and Khayyam, and then proceeded to prove many theorems under the assumption of an acute angle. Unlike Saccheri, he never felt that he had reached a contradiction with this assumption. He had proved the non-Euclidean result that the sum of the angles in a triangle increases as the area of the triangle decreases, and this led him to speculate on the possibility of a model of the acute case on a sphere of imaginary radius. He did not carry this idea any further.
At this time it was widely believed that the universe worked according to the principles of Euclidean geometry.
Discovery of non-Euclidean geometry
The beginning of the 19th century would finally witness decisive steps in the creation of non-Euclidean geometry. Circa 1813,Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refer ...
and independently around 1818, the German professor of law Ferdinand Karl Schweikart
Ferdinand Karl Schweikart (1780–1857) was a German jurist and amateur mathematician who developed an ''astral geometry'' before the discovery of non-Euclidean geometry.
Life and work
Schweikart, son of an attorney in Hesse, was educated in t ...
had the germinal ideas of non-Euclidean geometry worked out, but neither published any results. Schweikart's nephew Franz Taurinus did publish important results of hyperbolic trigonometry in two papers in 1825 and 1826, yet while admitting the internal consistency of hyperbolic geometry, he still believed in the special role of Euclidean geometry.
Then, in 1829–1830 the Russia
Russia (, , ), or the Russian Federation, is a List of transcontinental countries, transcontinental country spanning Eastern Europe and North Asia, Northern Asia. It is the List of countries and dependencies by area, largest country in the ...
n mathematician Nikolai Ivanovich Lobachevsky
Nikolai Ivanovich Lobachevsky ( rus, Никола́й Ива́нович Лобаче́вский, p=nʲikɐˈlaj ɪˈvanəvʲɪtɕ ləbɐˈtɕɛfskʲɪj, a=Ru-Nikolai_Ivanovich_Lobachevsky.ogg; – ) was a Russian mathematician and geometer, kn ...
and in 1832 the Hungarian mathematician János Bolyai
János Bolyai (; 15 December 1802 – 27 January 1860) or Johann Bolyai, was a Hungarian mathematician, who developed absolute geometry—a geometry that includes both Euclidean geometry and hyperbolic geometry. The discovery of a consisten ...
separately and independently published treatises on hyperbolic geometry. Consequently, hyperbolic geometry is called Lobachevskian or Bolyai-Lobachevskian geometry, as both mathematicians, independent of each other, are the basic authors of non-Euclidean geometry. Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refer ...
mentioned to Bolyai's father, when shown the younger Bolyai's work, that he had developed such a geometry several years before, though he did not publish. While Lobachevsky created a non-Euclidean geometry by negating the parallel postulate, Bolyai worked out a geometry where both the Euclidean and the hyperbolic geometry are possible depending on a parameter ''k''. Bolyai ends his work by mentioning that it is not possible to decide through mathematical reasoning alone if the geometry of the physical universe is Euclidean or non-Euclidean; this is a task for the physical sciences.
Bernhard Riemann
Georg Friedrich Bernhard Riemann (; 17 September 1826 – 20 July 1866) was a German mathematician who made contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the first rig ...
, in a famous lecture in 1854, founded the field of Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a ''Riemannian metric'', i.e. with an inner product on the tangent space at each point that varies smoothly from point to poin ...
, discussing in particular the ideas now called manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a n ...
s, Riemannian metric
In differential geometry, a Riemannian manifold or Riemannian space , so called after the German mathematician Bernhard Riemann, is a real, smooth manifold ''M'' equipped with a positive-definite inner product ''g'p'' on the tangent space '' ...
, and curvature.
He constructed an infinite family of non-Euclidean geometries by giving a formula for a family of Riemannian metrics on the unit ball in Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics ther ...
. The simplest of these is called elliptic geometry
Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines ...
and it is considered a non-Euclidean geometry due to its lack of parallel lines.
By formulating the geometry in terms of a curvature tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tenso ...
, Riemann allowed non-Euclidean geometry to apply to higher dimensions. Beltrami (1868) was the first to apply Riemann's geometry to spaces of negative curvature.
Terminology
It was Gauss who coined the term "non-Euclidean geometry". He was referring to his own work, which today we call ''hyperbolic geometry''. Several modern authors still consider ''non-Euclidean geometry'' and ''hyperbolic geometry'' synonyms. Arthur Cayley noted that distance between points inside a conic could be defined in terms oflogarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 o ...
and the projective cross-ratio
In geometry, the cross-ratio, also called the double ratio and anharmonic ratio, is a number associated with a list of four collinear points, particularly points on a projective line. Given four points ''A'', ''B'', ''C'' and ''D'' on a line, th ...
function. The method has become called the Cayley–Klein metric
In mathematics, a Cayley–Klein metric is a metric on the complement of a fixed quadric in a projective space which is defined using a cross-ratio. The construction originated with Arthur Cayley's essay "On the theory of distance"Cayley (1859), ...
because Felix Klein
Christian Felix Klein (; 25 April 1849 – 22 June 1925) was a German mathematician and mathematics educator, known for his work with group theory, complex analysis, non-Euclidean geometry, and on the associations between geometry and grou ...
exploited it to describe the non-Euclidean geometries in articles in 1871 and 1873 and later in book form. The Cayley–Klein metrics provided working models of hyperbolic and elliptic metric geometries, as well as Euclidean geometry.
Klein is responsible for the terms "hyperbolic" and "elliptic" (in his system he called Euclidean geometry ''parabolic'', a term that generally fell out of use). His influence has led to the current usage of the term "non-Euclidean geometry" to mean either "hyperbolic" or "elliptic" geometry.
There are some mathematicians who would extend the list of geometries that should be called "non-Euclidean" in various ways.
Axiomatic basis of non-Euclidean geometry
Euclidean geometry can be axiomatically described in several ways. Unfortunately, Euclid's original system of five postulates (axioms) is not one of these, as his proofs relied on several unstated assumptions that should also have been taken as axioms. Hilbert's system consisting of 20 axioms most closely follows the approach of Euclid and provides the justification for all of Euclid's proofs. Other systems, using different sets of undefined terms obtain the same geometry by different paths. All approaches, however, have an axiom that is logically equivalent to Euclid's fifth postulate, the parallel postulate.Hilbert
David Hilbert (; ; 23 January 1862 – 14 February 1943) was a German mathematician, one of the most influential mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many ...
uses the Playfair axiom form, while Birkhoff, for instance, uses the axiom that says that, "There exists a pair of similar but not congruent triangles." In any of these systems, removal of the one axiom equivalent to the parallel postulate, in whatever form it takes, and leaving all the other axioms intact, produces absolute geometry
Absolute geometry is a geometry based on an axiom system for Euclidean geometry without the parallel postulate or any of its alternatives. Traditionally, this has meant using only the first four of Euclid's postulates, but since these are not suf ...
. As the first 28 propositions of Euclid (in ''The Elements'') do not require the use of the parallel postulate or anything equivalent to it, they are all true statements in absolute geometry.
To obtain a non-Euclidean geometry, the parallel postulate (or its equivalent) ''must'' be replaced by its negation
In logic, negation, also called the logical complement, is an operation that takes a proposition P to another proposition "not P", written \neg P, \mathord P or \overline. It is interpreted intuitively as being true when P is false, and false ...
. Negating the Playfair's axiom
In geometry, Playfair's axiom is an axiom that can be used instead of the fifth postulate of Euclid (the parallel postulate):
''In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the ...
form, since it is a compound statement (... there exists one and only one ...), can be done in two ways:
* Either there will exist more than one line through the point parallel to the given line or there will exist no lines through the point parallel to the given line. In the first case, replacing the parallel postulate (or its equivalent) with the statement "In a plane, given a point P and a line not passing through P, there exist two lines through P, which do not meet " and keeping all the other axioms, yields hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P ...
.
* The second case is not dealt with as easily. Simply replacing the parallel postulate with the statement, "In a plane, given a point P and a line not passing through P, all the lines through P meet ", does not give a consistent set of axioms. This follows since parallel lines exist in absolute geometry, but this statement says that there are no parallel lines. This problem was known (in a different guise) to Khayyam, Saccheri and Lambert and was the basis for their rejecting what was known as the "obtuse angle case". To obtain a consistent set of axioms that includes this axiom about having no parallel lines, some other axioms must be tweaked. These adjustments depend upon the axiom system used. Among others, these tweaks have the effect of modifying Euclid's second postulate from the statement that line segments can be extended indefinitely to the statement that lines are unbounded. Riemann
Georg Friedrich Bernhard Riemann (; 17 September 1826 – 20 July 1866) was a German mathematician who made contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the first rig ...
's elliptic geometry
Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines ...
emerges as the most natural geometry satisfying this axiom.
Models of non-Euclidean geometry
 Two dimensional Euclidean geometry is
Two dimensional Euclidean geometry is modelled
A model is a person with a role either to promote, display or advertise commercial products (notably fashion clothing in fashion shows) or to serve as a visual aid for people who are creating works of art or to pose for photography. Though mo ...
by our notion of a "flat plane
Plane(s) most often refers to:
* Aero- or airplane, a powered, fixed-wing aircraft
* Plane (geometry), a flat, 2-dimensional surface
Plane or planes may also refer to:
Biology
* Plane (tree) or ''Platanus'', wetland native plant
* ''Planes' ...
".
Elliptic geometry
The simplest model forelliptic geometry
Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines ...
is a sphere, where lines are "great circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.
Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geomet ...
s" (such as the equator
The equator is a circle of latitude, about in circumference, that divides Earth into the Northern and Southern hemispheres. It is an imaginary line located at 0 degrees latitude, halfway between the North and South poles. The term can als ...
or the meridian
Meridian or a meridian line (from Latin ''meridies'' via Old French ''meridiane'', meaning “midday”) may refer to
Science
* Meridian (astronomy), imaginary circle in a plane perpendicular to the planes of the celestial equator and horizon
* ...
s on a globe
A globe is a spherical model of Earth, of some other celestial body, or of the celestial sphere. Globes serve purposes similar to maps, but unlike maps, they do not distort the surface that they portray except to scale it down. A model globe ...
), and points opposite each other (called antipodal points
In mathematics, antipodal points of a sphere are those diametrically opposite to each other (the specific qualities of such a definition are that a line drawn from the one to the other passes through the center of the sphere so forms a true ...
) are identified (considered the same). This is also one of the standard models of the real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold; in other words, a one-sided surface. It cannot be embedded in standard three-dimensional space without intersecting itself. It has b ...
. The difference is that as a model of elliptic geometry a metric is introduced permitting the measurement of lengths and angles, while as a model of the projective plane there is no such metric.
In the elliptic model, for any given line and a point ''A'', which is not on , all lines through ''A'' will intersect .
Hyperbolic geometry
Even after the work of Lobachevsky, Gauss, and Bolyai, the question remained: "Does such a model exist forhyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P ...
?". The model for hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P ...
was answered by Eugenio Beltrami, in 1868, who first showed that a surface called the pseudosphere
In geometry, a pseudosphere is a surface with constant negative Gaussian curvature.
A pseudosphere of radius is a surface in \mathbb^3 having curvature in each point. Its name comes from the analogy with the sphere of radius , which is a surface ...
has the appropriate curvature to model a portion of hyperbolic space
In mathematics, hyperbolic space of dimension n is the unique simply connected, n-dimensional Riemannian manifold of constant sectional curvature equal to -1. It is homogeneous, and satisfies the stronger property of being a symmetric space. The ...
and in a second paper in the same year, defined the Klein model
Klein may refer to:
People
* Klein (surname)
*Klein (musician)
Places
* Klein (crater), a lunar feature
* Klein, Montana, United States
*Klein, Texas, United States
*Klein (Ohm), a river of Hesse, Germany, tributary of the Ohm
*Klein River, a ri ...
, which models the entirety of hyperbolic space, and used this to show that Euclidean geometry and hyperbolic geometry were equiconsistent
In mathematical logic, two theories are equiconsistent if the consistency of one theory implies the consistency of the other theory, and vice versa. In this case, they are, roughly speaking, "as consistent as each other".
In general, it is not p ...
so that hyperbolic geometry was logically consistent
In classical deductive logic, a consistent theory is one that does not lead to a logical contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent ...
if and only if Euclidean geometry was. (The reverse implication follows from the horosphere
In hyperbolic geometry, a horosphere (or parasphere) is a specific hypersurface in hyperbolic ''n''-space. It is the boundary of a horoball, the limit of a sequence of increasing balls sharing (on one side) a tangent hyperplane and its point of ...
model of Euclidean geometry.)
In the hyperbolic model, within a two-dimensional plane, for any given line and a point ''A'', which is not on , there are infinitely
Infinity is that which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .
Since the time of the ancient Greeks, the philosophical nature of infinity was the subject of many discussions amo ...
many lines through ''A'' that do not intersect .
In these models, the concepts of non-Euclidean geometries are represented by Euclidean objects in a Euclidean setting. This introduces a perceptual distortion wherein the straight lines of the non-Euclidean geometry are represented by Euclidean curves that visually bend. This "bending" is not a property of the non-Euclidean lines, only an artifice of the way they are represented.
Three-dimensional non-Euclidean geometry
In three dimensions, there are eight models of geometries. There are Euclidean, elliptic, and hyperbolic geometries, as in the two-dimensional case; mixed geometries that are partially Euclidean and partially hyperbolic or spherical; twisted versions of the mixed geometries; and one unusual geometry that is completelyanisotropic
Anisotropy () is the property of a material which allows it to change or assume different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's physic ...
(i.e. every direction behaves differently).
Uncommon properties
absolute geometry
Absolute geometry is a geometry based on an axiom system for Euclidean geometry without the parallel postulate or any of its alternatives. Traditionally, this has meant using only the first four of Euclid's postulates, but since these are not suf ...
(also called ''neutral geometry''). However, the properties that distinguish one geometry from others have historically received the most attention.
Besides the behavior of lines with respect to a common perpendicular, mentioned in the introduction, we also have the following:
* A Lambert quadrilateral
In geometry, a Lambert quadrilateral (also known as Ibn al-Haytham–Lambert quadrilateral), is a quadrilateral in which three of its angles are right angles. Historically, the fourth angle of a Lambert quadrilateral was of considerable interest s ...
is a quadrilateral with three right angles. The fourth angle of a Lambert quadrilateral is acute
Acute may refer to:
Science and technology
* Acute angle
** Acute triangle
** Acute, a leaf shape in the glossary of leaf morphology
* Acute (medicine), a disease that it is of short duration and of recent onset.
** Acute toxicity, the adverse eff ...
if the geometry is hyperbolic, a right angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the ad ...
if the geometry is Euclidean or obtuse if the geometry is elliptic. Consequently, rectangle
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containi ...
s exist (a statement equivalent to the parallel postulate) only in Euclidean geometry.
* A Saccheri quadrilateral
A Saccheri quadrilateral (also known as a Khayyam–Saccheri quadrilateral) is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book ''Euclides ab omni na ...
is a quadrilateral with two sides of equal length, both perpendicular to a side called the ''base''. The other two angles of a Saccheri quadrilateral are called the ''summit angles'' and they have equal measure. The summit angles of a Saccheri quadrilateral are acute if the geometry is hyperbolic, right angles if the geometry is Euclidean and obtuse angles if the geometry is elliptic.
* The sum of the measures of the angles of any triangle is less than 180° if the geometry is hyperbolic, equal to 180° if the geometry is Euclidean, and greater than 180° if the geometry is elliptic. The ''defect'' of a triangle is the numerical value (180° − sum of the measures of the angles of the triangle). This result may also be stated as: the defect of triangles in hyperbolic geometry is positive, the defect of triangles in Euclidean geometry is zero, and the defect of triangles in elliptic geometry is negative.
Importance
Before the models of a non-Euclidean plane were presented by Beltrami, Klein, and Poincaré, Euclidean geometry stood unchallenged as themathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences (such as physics, ...
of space
Space is the boundless three-dimensional extent in which objects and events have relative position and direction. In classical physics, physical space is often conceived in three linear dimensions, although modern physicists usually cons ...
. Furthermore, since the substance of the subject in synthetic geometry
Synthetic geometry (sometimes referred to as axiomatic geometry or even pure geometry) is the study of geometry without the use of coordinates or formulae. It relies on the axiomatic method and the tools directly related to them, that is, compa ...
was a chief exhibit of rationality, the Euclidean point of view represented absolute authority.
The discovery of the non-Euclidean geometries had a ripple effect which went far beyond the boundaries of mathematics and science. The philosopher Immanuel Kant
Immanuel Kant (, , ; 22 April 1724 – 12 February 1804) was a German philosopher and one of the central Enlightenment thinkers. Born in Königsberg, Kant's comprehensive and systematic works in epistemology, metaphysics, ethics, and ...
's treatment of human knowledge had a special role for geometry. It was his prime example of synthetic a priori knowledge; not derived from the senses nor deduced through logic — our knowledge of space was a truth that we were born with. Unfortunately for Kant, his concept of this unalterably true geometry was Euclidean. Theology was also affected by the change from absolute truth to relative truth in the way that mathematics is related to the world around it, that was a result of this paradigm shift.
Non-Euclidean geometry is an example of a scientific revolution
The Scientific Revolution was a series of events that marked the emergence of modern science during the early modern period, when developments in mathematics, physics, astronomy, biology (including human anatomy) and chemistry transfo ...
in the history of science
The history of science covers the development of science from ancient times to the present. It encompasses all three major branches of science: natural, social, and formal.
Science's earliest roots can be traced to Ancient Egypt and Meso ...
, in which mathematicians and scientists changed the way they viewed their subjects. Some geometers called Lobachevsky
Nikolai Ivanovich Lobachevsky ( rus, Никола́й Ива́нович Лобаче́вский, p=nʲikɐˈlaj ɪˈvanəvʲɪtɕ ləbɐˈtɕɛfskʲɪj, a=Ru-Nikolai_Ivanovich_Lobachevsky.ogg; – ) was a Russian mathematician and geometer, kn ...
the "Copernicus
Nicolaus Copernicus (; pl, Mikołaj Kopernik; gml, Niklas Koppernigk, german: Nikolaus Kopernikus; 19 February 1473 – 24 May 1543) was a Renaissance polymath, active as a mathematician, astronomer, and Catholic canon, who formulated ...
of Geometry" due to the revolutionary character of his work.
The existence of non-Euclidean geometries impacted the intellectual life of Victorian England
In the history of the United Kingdom and the British Empire, the Victorian era was the period of Queen Victoria's reign, from 20 June 1837 until her death on 22 January 1901. The era followed the Georgian period and preceded the Edwardia ...
in many ways and in particular was one of the leading factors that caused a re-examination of the teaching of geometry based on Euclid's Elements
The ''Elements'' ( grc, Στοιχεῖα ''Stoikheîa'') is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid in Alexandria, Ptolemaic Egypt 300 BC. It is a collection of definitions, postulat ...
. This curriculum issue was hotly debated at the time and was even the subject of a book, '' Euclid and his Modern Rivals'', written by Charles Lutwidge Dodgson (1832–1898) better known as Lewis Carroll
Charles Lutwidge Dodgson (; 27 January 1832 – 14 January 1898), better known by his pen name Lewis Carroll, was an English author, poet and mathematician. His most notable works are ''Alice's Adventures in Wonderland'' (1865) and its sequel ...
, the author of '' Alice in Wonderland''.
Planar algebras
Inanalytic geometry
In classical mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineerin ...
a plane
Plane(s) most often refers to:
* Aero- or airplane, a powered, fixed-wing aircraft
* Plane (geometry), a flat, 2-dimensional surface
Plane or planes may also refer to:
Biology
* Plane (tree) or ''Platanus'', wetland native plant
* ''Planes' ...
is described with Cartesian coordinate
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in ...
s : ''C'' = . The point
Point or points may refer to:
Places
* Point, Lewis, a peninsula in the Outer Hebrides, Scotland
* Point, Texas, a city in Rains County, Texas, United States
* Point, the NE tip and a ferry terminal of Lismore, Inner Hebrides, Scotland
* Point ...
s are sometimes identified with complex numbers where ε2 ∈ .
The Euclidean plane corresponds to the case since the modulus of is given by
:
and this quantity is the square of the Euclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points.
It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefor ...
between and the origin.
For instance, is the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
.
For planar algebra, non-Euclidean geometry arises in the other cases.
When , then is a split-complex number and conventionally replaces epsilon. Then
:
and is the unit hyperbola
In geometry, the unit hyperbola is the set of points (''x'',''y'') in the Cartesian plane that satisfy the implicit equation x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an ''alternative radi ...
.
When , then is a dual number
In algebra, the dual numbers are a hypercomplex number system first introduced in the 19th century. They are expressions of the form , where and are real numbers, and is a symbol taken to satisfy \varepsilon^2 = 0 with \varepsilon\neq 0.
Du ...
.
This approach to non-Euclidean geometry explains the non-Euclidean angles: the parameters of slope
In mathematics, the slope or gradient of a line is a number that describes both the ''direction'' and the ''steepness'' of the line. Slope is often denoted by the letter ''m''; there is no clear answer to the question why the letter ''m'' is use ...
in the dual number plane and hyperbolic angle
In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of ''xy'' = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrises the unit hyperbola, which has hyperbolic function ...
in the split-complex plane correspond to angle
In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle.
Angles formed by two ...
in Euclidean geometry. Indeed, they each arise in polar decomposition
In mathematics, the polar decomposition of a square real or complex matrix A is a factorization of the form A = U P, where U is an orthogonal matrix and P is a positive semi-definite symmetric matrix (U is a unitary matrix and P is a positive se ...
of a complex number .
Kinematic geometries
Hyperbolic geometry found an application inkinematics
Kinematics is a subfield of physics, developed in classical mechanics, that describes the Motion (physics), motion of points, Physical object, bodies (objects), and systems of bodies (groups of objects) without considering the forces that cause ...
with the physical cosmology
Physical cosmology is a branch of cosmology concerned with the study of cosmological models. A cosmological model, or simply cosmology, provides a description of the largest-scale structures and dynamics of the universe and allows study of f ...
introduced by Hermann Minkowski
Hermann Minkowski (; ; 22 June 1864 – 12 January 1909) was a German mathematician and professor at Königsberg, Zürich and Göttingen. He created and developed the geometry of numbers and used geometrical methods to solve problems in number t ...
in 1908. Minkowski introduced terms like worldline
The world line (or worldline) of an object is the path that an object traces in 4-dimensional spacetime. It is an important concept in modern physics, and particularly theoretical physics.
The concept of a "world line" is distinguished from con ...
and proper time
In relativity, proper time (from Latin, meaning ''own time'') along a timelike world line is defined as the time as measured by a clock following that line. It is thus independent of coordinates, and is a Lorentz scalar. The proper time interval ...
into mathematical physics
Mathematical physics refers to the development of mathematics, mathematical methods for application to problems in physics. The ''Journal of Mathematical Physics'' defines the field as "the application of mathematics to problems in physics and t ...
. He realized that the submanifold
In mathematics, a submanifold of a manifold ''M'' is a subset ''S'' which itself has the structure of a manifold, and for which the inclusion map satisfies certain properties. There are different types of submanifolds depending on exactly which ...
, of events one moment of proper time into the future, could be considered a hyperbolic space
In mathematics, hyperbolic space of dimension n is the unique simply connected, n-dimensional Riemannian manifold of constant sectional curvature equal to -1. It is homogeneous, and satisfies the stronger property of being a symmetric space. The ...
of three dimensions.
Already in the 1890s Alexander Macfarlane
Alexander Macfarlane FRSE LLD (21 April 1851 – 28 August 1913) was a Scottish logician, physicist, and mathematician.
Life
Macfarlane was born in Blairgowrie, Scotland, to Daniel MacFarlane (Shoemaker, Blairgowire) and Ann Small. He s ...
was charting this submanifold through his Algebra of Physics and hyperbolic quaternion
In abstract algebra, the algebra of hyperbolic quaternions is a nonassociative algebra over the real numbers with elements of the form
:q = a + bi + cj + dk, \quad a,b,c,d \in \mathbb \!
where the squares of i, j, and k are +1 and distinct eleme ...
s, though Macfarlane did not use cosmological language as Minkowski did in 1908. The relevant structure is now called the hyperboloid model
In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski, is a model of ''n''-dimensional hyperbolic geometry in which points are represented by points on the forward sheet ''S''+ of a two-sheeted hyperbolo ...
of hyperbolic geometry.
The non-Euclidean planar algebras support kinematic geometries in the plane. For instance, the split-complex number ''z'' = e''a''j can represent a spacetime event one moment into the future of a frame of reference of rapidity
In relativity, rapidity is commonly used as a measure for relativistic velocity. Mathematically, rapidity can be defined as the hyperbolic angle that differentiates two frames of reference in relative motion, each frame being associated with di ...
''a''. Furthermore, multiplication by ''z'' amounts to a Lorentz boost
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation i ...
mapping the frame with rapidity zero to that with rapidity ''a''.
Kinematic study makes use of the dual number
In algebra, the dual numbers are a hypercomplex number system first introduced in the 19th century. They are expressions of the form , where and are real numbers, and is a symbol taken to satisfy \varepsilon^2 = 0 with \varepsilon\neq 0.
Du ...
s to represent the classical description of motion in absolute time and space:
The equations are equivalent to a shear mapping
In plane geometry, a shear mapping is a linear map that displaces each point in a fixed direction, by an amount proportional to its signed distance from the line that is parallel to that direction and goes through the origin. This type of mappi ...
in linear algebra:
:
With dual numbers the mapping is
Another view of special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates:
# The laws o ...
as a non-Euclidean geometry was advanced by E. B. Wilson and Gilbert Lewis in ''Proceedings of the American Academy of Arts and Sciences
The American Academy of Arts and Sciences (abbreviation: AAA&S) is one of the oldest learned societies in the United States. It was founded in 1780 during the American Revolution by John Adams, John Hancock, James Bowdoin, Andrew Oliver, and ...
'' in 1912. They revamped the analytic geometry implicit in the split-complex number algebra into synthetic geometry
Synthetic geometry (sometimes referred to as axiomatic geometry or even pure geometry) is the study of geometry without the use of coordinates or formulae. It relies on the axiomatic method and the tools directly related to them, that is, compa ...
of premises and deductions.
Fiction
Non-Euclidean geometry often makes appearances in works ofscience fiction
Science fiction (sometimes shortened to Sci-Fi or SF) is a genre of speculative fiction which typically deals with imaginative and futuristic concepts such as advanced science and technology, space exploration, time travel, parallel unive ...
and fantasy
Fantasy is a genre of speculative fiction involving Magic (supernatural), magical elements, typically set in a fictional universe and sometimes inspired by mythology and folklore. Its roots are in oral traditions, which then became fantasy ...
.
* In 1895, H. G. Wells
Herbert George Wells"Wells, H. G."
Revised 18 May 2015. ''
Hyperbolic geometry: The first 150 years
', Bull. Amer. Math. Soc. (N.S.) Volume 6, Number 1, pp. 9–24. * * * Stewart, Ian (2001) ''
Non-Euclidean Geometry
Open Court, Chicago.
*
Non-Euclidean geometries
from ''Encyclopedia of Math'' of
Synthetic Spacetime
a digest of the axioms used, and theorems proved, by Wilson and Lewis. Archived by
Revised 18 May 2015. ''
antipodal points
In mathematics, antipodal points of a sphere are those diametrically opposite to each other (the specific qualities of such a definition are that a line drawn from the one to the other passes through the center of the sphere so forms a true ...
on a sphere are identified in a model of the elliptic plane. In the story, in the midst of a thunderstorm, Sidney Davidson sees "Waves and a remarkably neat schooner" while working in an electrical laboratory at Harlow Technical College. At the story's close, Davidson proves to have witnessed H.M.S. ''Fulmar'' off Antipodes Island
In geography, the antipode () of any spot on Earth is the point on Earth's surface diametrically opposite to it. A pair of points ''antipodal'' () to each other are situated such that a straight line connecting the two would pass through Ear ...
.
* Non-Euclidean geometry is sometimes connected with the influence of the 20th-century horror fiction
Horror is a genre of fiction which is intended to frighten, scare, or disgust. Horror is often divided into the sub-genres of psychological horror and supernatural horror, which is in the realm of speculative fiction. Literary historian J ...
writer H. P. Lovecraft. In his works, many unnatural things follow their own unique laws of geometry: in Lovecraft's Cthulhu Mythos
The Cthulhu Mythos is a mythopoeia and a shared fictional universe, originating in the works of American horror writer H. P. Lovecraft. The term was coined by August Derleth
August William Derleth (February 24, 1909 – July 4, 1971) was an ...
, the sunken city of R'lyeh
R'lyeh is a fictional lost city that was first mentioned in the H. P. Lovecraft short story "The Call of Cthulhu", first published in ''Weird Tales'' in February 1928. R'lyeh is a sunken city in the South Pacific and the prison of the entity calle ...
is characterized by its non-Euclidean geometry. It is heavily implied this is achieved as a side effect of not following the natural laws of this universe rather than simply using an alternate geometric model, as the sheer innate wrongness of it is said to be capable of driving those who look upon it insane.
* The main character in Robert Pirsig
Robert Maynard Pirsig (; September 6, 1928 – April 24, 2017) was an American writer and philosopher. He was the author of the philosophical novels '' Zen and the Art of Motorcycle Maintenance: An Inquiry into Values'' (1974) and '' Lila: ...
's ''Zen and the Art of Motorcycle Maintenance
''Zen and the Art of Motorcycle Maintenance: An Inquiry into Values'' is a book by Robert M. Pirsig first published in 1974. It is a work of fictionalized autobiography and is the first of Pirsig's texts in which he explores his concept of Qua ...
'' mentioned Riemannian Geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a ''Riemannian metric'', i.e. with an inner product on the tangent space at each point that varies smoothly from point to poin ...
on multiple occasions.
* In ''The Brothers Karamazov
''The Brothers Karamazov'' (russian: Братья Карамазовы, ''Brat'ya Karamazovy'', ), also translated as ''The Karamazov Brothers'', is the last novel by Russian author Fyodor Dostoevsky. Dostoevsky spent nearly two years writing '' ...
'', Dostoevsky discusses non-Euclidean geometry through his character Ivan.
* Christopher Priest's novel ''Inverted World
''Inverted World'' (''The Inverted World'' in some editions) is a 1974 science fiction novel by British writer Christopher Priest. The novel's basic premise was first used in the short story "The Inverted World" included in '' New Writings in ...
'' describes the struggle of living on a planet with the form of a rotating pseudosphere
In geometry, a pseudosphere is a surface with constant negative Gaussian curvature.
A pseudosphere of radius is a surface in \mathbb^3 having curvature in each point. Its name comes from the analogy with the sphere of radius , which is a surface ...
.
* Robert Heinlein's '' The Number of the Beast'' utilizes non-Euclidean geometry to explain instantaneous transport through space and time and between parallel and fictional universes.
* Zeno Rogue's ''HyperRogue
''HyperRogue'' is an independent video game developed by Zeno Rogue. It is a roguelike inspired by the puzzle game ''Deadly Rooms of Death'' and the art of M. C. Escher, taking place in the hyperbolic plane.
Gameplay
''HyperRogue'' is a t ...
'' is a roguelike
Roguelike (or rogue-like) is a subgenre of role-playing computer games traditionally characterized by a dungeon crawl through procedurally generated levels, turn-based gameplay, grid-based movement, and permanent death of the player charac ...
game set on the hyperbolic plane
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai– Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P' ...
, allowing the player to experience many properties of this geometry. Many mechanics, quests, and locations are strongly dependent on the features of hyperbolic geometry.
* In the Renegade Legion
''Renegade Legion'' is a series of science fiction games that were designed by Sam Lewis, produced by FASA, and published from 1989 to 1993. The line was then licensed to Nightshift games, a spin-off of the garage company Crunchy Frog Enterpris ...
science fiction
Science fiction (sometimes shortened to Sci-Fi or SF) is a genre of speculative fiction which typically deals with imaginative and futuristic concepts such as advanced science and technology, space exploration, time travel, parallel unive ...
setting for FASA
Fasa ( fa, فسا, Fasā, also Romanized as Fassa) is a city and capital of Fasa County, Fars Province, Iran. At the 2016 census, its population was 110,825, in 33,379 families. Fasa is the fourth most populous city of the province. The city date ...
's wargame
A wargame is a strategy game in which two or more players command opposing armed forces in a realistic simulation of an armed conflict. Wargaming may be played for recreation, to train military officers in the art of strategic thinking, or to s ...
, role-playing-game
A role-playing game (sometimes spelled roleplaying game, RPG) is a game in which players assume the roles of characters in a fictional setting. Players take responsibility for acting out these roles within a narrative, either through literal a ...
and fiction, faster-than-light travel
Faster-than-light (also FTL, superluminal or supercausal) travel and communication are the conjectural propagation of matter or information faster than the speed of light (). The special theory of relativity implies that only particles with zero ...
and communications is possible through the use of Hsieh Ho's Polydimensional Non-Euclidean Geometry, published sometime in the middle of the 22nd century.
* In Ian Stewart's ''Flatterland
''Flatterland'' is a 2001 book written by mathematician and science popularizer Ian Stewart about non-Euclidean geometry. It was written as a sequel to ''Flatland'', an 1884 novel that discussed different dimensions.
Plot summary
Almost 100 ...
'' the protagonist
A protagonist () is the main character of a story. The protagonist makes key decisions that affect the plot, primarily influencing the story and propelling it forward, and is often the character who faces the most significant obstacles. If a st ...
Victoria Line visits all kinds of non-Euclidean worlds.
See also
*Hyperbolic space
In mathematics, hyperbolic space of dimension n is the unique simply connected, n-dimensional Riemannian manifold of constant sectional curvature equal to -1. It is homogeneous, and satisfies the stronger property of being a symmetric space. The ...
* Lénárt sphere
A Lénárt sphere is a educational manipulative and writing surface for exploring spherical geometry, invented by Hungarian István Lénárt as a modern replacement for a spherical blackboard. It can be used for visualizing the geometry of po ...
* Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, ...
*Non-Euclidean surface growth A number of processes of surface growth in areas ranging from mechanics of growing gravitational bodies through propagating fronts of phase transitions, epitaxial growth of nanostructures and 3D printing, growth of plants, and cell mobility require ...
Notes
References
*, (2012) ''Notes on hyperbolic geometry'', in: Strasbourg Master class on Geometry, pp. 1–182, IRMA Lectures in Mathematics and Theoretical Physics, Vol. 18, Zürich: European Mathematical Society (EMS), 461 pages, , DOI:10.4171/105. * Anderson, James W. ''Hyperbolic Geometry'', second edition, Springer, 2005 * Beltrami, Eugenio ''Teoria fondamentale degli spazî di curvatura costante'', Annali. di Mat., ser II 2 (1868), 232–255 * * Carroll, Lewis ''Euclid and His Modern Rivals'', New York: Barnes and Noble, 2009 (reprint) * H. S. M. Coxeter (1942) ''Non-Euclidean Geometry'',University of Toronto Press
The University of Toronto Press is a Canadian university press founded in 1901. Although it was founded in 1901, the press did not actually publish any books until 1911.
The press originally printed only examination books and the university cale ...
, reissued 1998 by Mathematical Association of America, .
*
* Jeremy Gray (1989) ''Ideas of Space: Euclidean, Non-Euclidean, and Relativistic'', 2nd edition, Clarendon Press
Oxford University Press (OUP) is the university press of the University of Oxford. It is the largest university press in the world, and its printing history dates back to the 1480s. Having been officially granted the legal right to print books ...
.
* Greenberg, Marvin Jay
Marvin Jay Greenberg (December 22, 1935 – December 12, 2017) was an American mathematician.
Education
Greenberg studied at Columbia University where he received his bachelor's degree in 1955 (he was a Ford Scholar as an undergraduate) and ...
''Euclidean and Non-Euclidean Geometries: Development and History'', 4th ed., New York: W. H. Freeman, 2007.
* Morris Kline
Morris Kline (May 1, 1908 – June 10, 1992) was a professor of mathematics, a writer on the history, philosophy, and teaching of mathematics, and also a popularizer of mathematical subjects.
Education and career
Kline was born to a Jewish fami ...
(1972) ''Mathematical Thought from Ancient to Modern Times'', Chapter 36 Non-Euclidean Geometry, pp 861–81, Oxford University Press
Oxford University Press (OUP) is the university press of the University of Oxford. It is the largest university press in the world, and its printing history dates back to the 1480s. Having been officially granted the legal right to print books ...
.
* Bernard H. Lavenda, (2012) " A New Perspective on Relativity : An Odyssey In Non-Euclidean Geometries", World Scientific
World Scientific Publishing is an academic publisher of scientific, technical, and medical books and journals headquartered in Singapore. The company was founded in 1981. It publishes about 600 books annually, along with 135 journals in various ...
, pp. 696, .
* Nikolai Lobachevsky
Nikolai Ivanovich Lobachevsky ( rus, Никола́й Ива́нович Лобаче́вский, p=nʲikɐˈlaj ɪˈvanəvʲɪtɕ ləbɐˈtɕɛfskʲɪj, a=Ru-Nikolai_Ivanovich_Lobachevsky.ogg; – ) was a Russian mathematician and geometer, kn ...
(2010) ''Pangeometry'', Translator and Editor: A. Papadopoulos, Heritage of European Mathematics Series, Vol. 4, European Mathematical Society
The European Mathematical Society (EMS) is a European organization dedicated to the development of mathematics in Europe. Its members are different mathematical societies in Europe, academic institutions and individual mathematicians. The current ...
.
*
*
* Milnor, John W. (1982) Hyperbolic geometry: The first 150 years
', Bull. Amer. Math. Soc. (N.S.) Volume 6, Number 1, pp. 9–24. * * * Stewart, Ian (2001) ''
Flatterland
''Flatterland'' is a 2001 book written by mathematician and science popularizer Ian Stewart about non-Euclidean geometry. It was written as a sequel to ''Flatland'', an 1884 novel that discussed different dimensions.
Plot summary
Almost 100 ...
'', New York: Perseus Publishing (softcover)
* John Stillwell
John Colin Stillwell (born 1942) is an Australian mathematician on the faculties of the University of San Francisco and Monash University.
Biography
He was born in Melbourne, Australia and lived there until he went to the Massachusetts Instit ...
(1996) ''Sources of Hyperbolic Geometry'', American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, ...
.
*
* A. Papadopoulos et Guillaume Théret
A is the first letter of the Latin and English alphabet.
A may also refer to:
Science and technology Quantities and units
* ''a'', a measure for the attraction between particles in the Van der Waals equation
* ''A'' value, a measure of ...
(2014) ''La théorie des parallèles de Johann Heinrich Lambert'', (Critical edition of Lambert's memoir with a French translation, with historical and mathematical notes and commentaries éd. Blanchard, coll. Sciences dans l'Histoire, Paris
External links
* *Roberto Bonola (1912Non-Euclidean Geometry
Open Court, Chicago.
*
Non-Euclidean geometries
from ''Encyclopedia of Math'' of
European Mathematical Society
The European Mathematical Society (EMS) is a European organization dedicated to the development of mathematics in Europe. Its members are different mathematical societies in Europe, academic institutions and individual mathematicians. The current ...
and Springer Science+Business Media
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing.
Originally founded in 1842 in ...
Synthetic Spacetime
a digest of the axioms used, and theorems proved, by Wilson and Lewis. Archived by
WebCite
WebCite was an on-demand archive site, designed to digitally preserve scientific and educationally important material on the web by taking snapshots of Internet contents as they existed at the time when a blogger or a scholar cited or quoted ...
.
{{DEFAULTSORT:Non-Euclidean Geometry